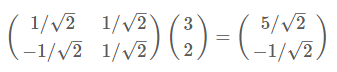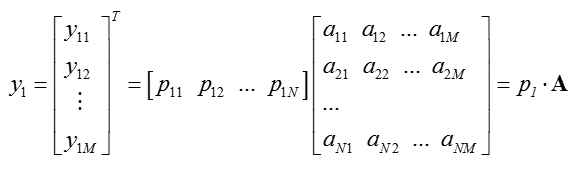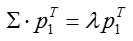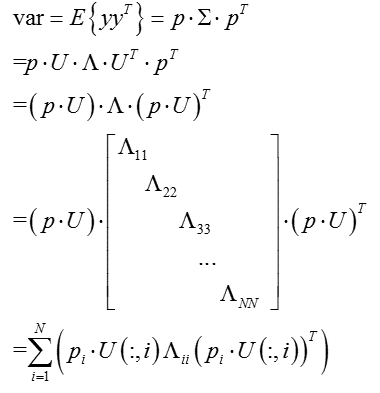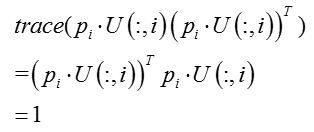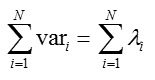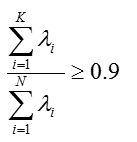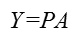作者:桂。
时间:2017-02-26 19:54:26
链接:http://www.cnblogs.com/xingshansi/articles/6445625.html
前言
本文为模式识别系列第一篇,主要介绍主成分分析算法(Principal Component Analysis,PCA)的理论,并附上相关代码。全文主要分六个部分展开:
1)简单示例。通过简单的例子,引出PCA算法;
2)理论推导。主要介绍PCA算法的理论推导以及对应的数学含义;
3)算法步骤。主要介绍PCA算法的算法流程;
4)应用实例。针对PCA的实际应用,列出两个应用实例;
5)常见问题补充。对于数据预处理过程中常遇到的问题进行补充;
6)扩展阅读。简要介绍PCA的不足,并给出K-L变换、Kernel-PCA(KPCA)的相关链接。
本文为个人总结,内容多有不当之处,麻烦各位批评指正。
一、简单示例
A-示例1:降维
先来看一组学生的成绩
| 学生1 | 学生2 | 学生3 | 学生4 | … | 学生N | |
| 语文成绩 | 85 | 85 | 85 | 85 | … | 85 |
| 数学成绩 | 96 | 93 | 78 | 64 | … | 97 |
为了方便分析,我们假设N=5;
| 学生1 | 学生2 | 学生3 | 学生4 | 学生5 | |
| 语文成绩 | 85 | 85 | 85 | 85 | 85 |
| 数学成绩 | 96 | 93 | 78 | 64 | 97 |
问题:现在要求大家将成绩与不同学生进行匹配。
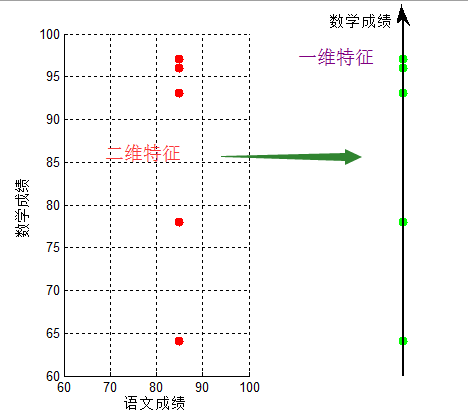
按【学生,语文成绩,数学成绩】进行匹配,即:【学生1,85,96】…【学生5,85,97】,可以看到,对于成绩【85,97】,我们很容易匹配出学生5;但仔细观察,他们的语文成绩都是相同的,即仅仅用数学成绩就可以表达出不同学生,即将数据从二维投影至一维
将【语文成绩,数学成绩】压缩成只用【数学成绩】,实现了数据降维,我们将【语文成绩,数学成绩】的二维特征,压缩成【数学成绩】的一维特征,这就是降维。
B-主成分分析
细心的同学,从上一个图中可以发现:将数据沿方差最大方向投影,数据更易于区分——这就是PCA降维的核心思想。上一个图的误差最大方向即是沿x轴方向。
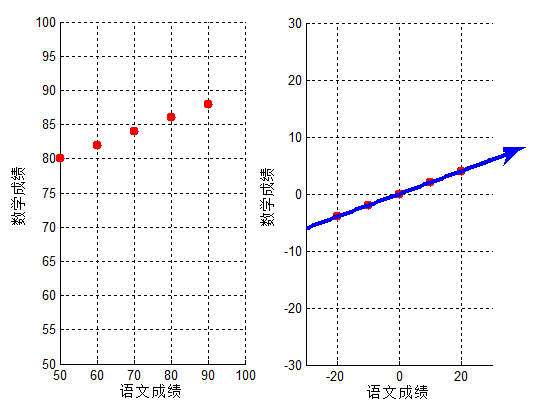
在进行理论推导以前,再看一个例子,还是之前5个同学的成绩,只不过这次测试他们语文成绩也不再相同:
| 学生1 | 学生2 | 学生3 | 学生4 | 学生5 | |
| 语文成绩 | 50 | 60 | 70 | 80 | 90 |
| 数学成绩 | 80 | 82 | 84 | 86 | 88 |
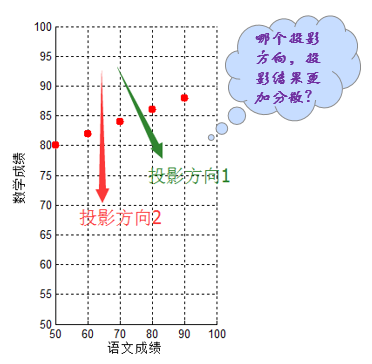
此时如果将二维特征【语文成绩,数学成绩】压缩成1维,仅仅用数学成绩表达似乎不是最佳方案,即使沿着投影方向2,只用语文成绩表达,其分散程度似乎也比不上投影方向1的降维结果。
如何找到最佳的(方差最大,即最分散。这也容易理解,毕竟分散的数据更容易区分开来)降维方式呢?显然最佳方案不总是用语文/数学成绩单一替代,这便需要本文的主角——PCA算法。简而言之:PCA算法其表现形式是降维,同时也是一种特征融合算法。
二、理论推导
进行正式的理论推导之前,先交代几个常用操作的几何意义。
A-内积与投影
下面先来看一个高中就学过的向量运算:内积。两个维数相同的向量的内积被定义为:
$(a_1,a_2,\cdots,a_n)^\mathsf{T}\cdot (b_1,b_2,\cdots,b_n)^\mathsf{T}=a_1b_1+a_2b_2+\cdots+a_nb_n$
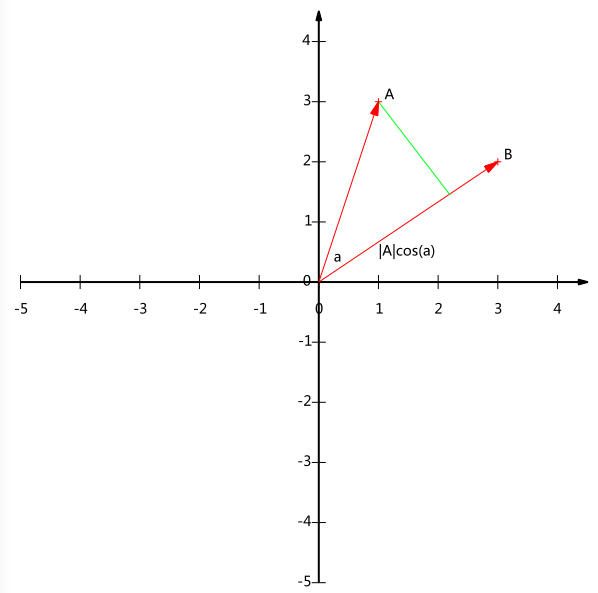
内积运算将两个向量映射为一个实数。其计算方式非常容易理解,但是其意义并不明显。下面我们分析内积的几何意义。假设A和B是两个n维向量,我们知道n维向量可以等价表示为n维空间中的一条从原点发射的有向线段,为了简单起见我们假设A和B均为二维向量,则$A=(x_1,y_1), B=(x_2,y_2)$。则在二维平面上A和B可以用两条发自原点的有向线段表示,见下图:
现在我们从A点向B所在直线引一条垂线。我们知道垂线与B的交点叫做A在B上的投影,再设A与B的夹角是a,则投影的矢量长度为$|A|cos(a)$,其中$|A|=\sqrt{x_1^2+y_1^2}$是向量A的模,也就是A线段的标量长度。
注意这里我们专门区分了矢量长度和标量长度,标量长度总是大于等于0,值就是线段的长度;而矢量长度可能为负,其绝对值是线段长度,而符号取决于其方向与标准方向相同或相反。
到这里还是看不出内积和这东西有什么关系,不过如果我们将内积表示为另一种我们熟悉的形式:
$A\cdot B=|A||B|cos(a)$
现在事情似乎是有点眉目了:A与B的内积等于A到B的投影长度乘以B的模。再进一步,如果我们假设B的模为1,即让$|B|=1$,那么就变成了:
$A\cdot B=|A|cos(a)$
也就是说,设向量B的模为1,则A与B的内积值等于A向B所在直线投影的矢量长度!这就是内积的一种几何解释,也是我们得到的第一个重要结论。在后面的推导中,将反复使用这个结论。
B-基的概念
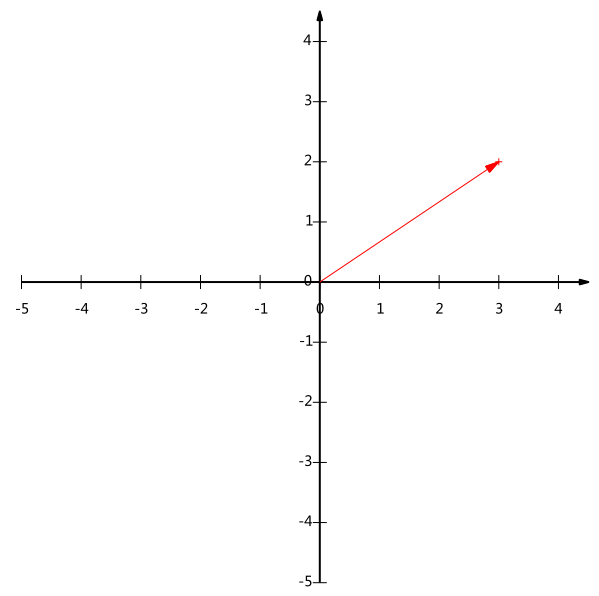
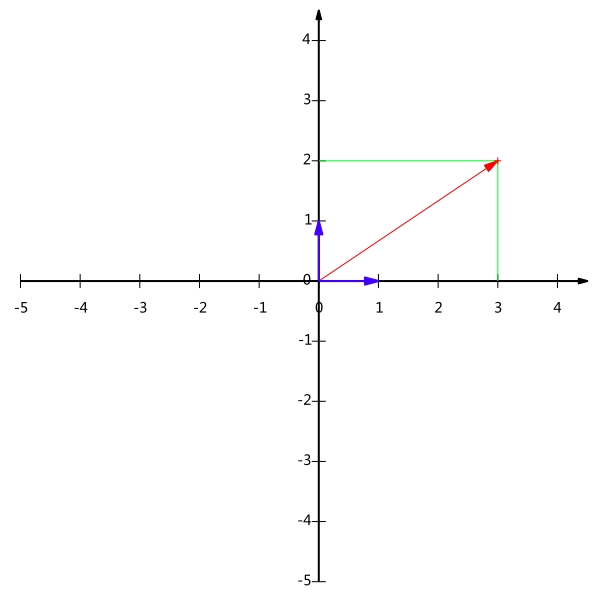
给出下面这个向量:
在代数表示方面,我们经常用线段终点的点坐标表示向量,例如上面的向量可以表示为(3,2),这是我们再熟悉不过的向量表示。
不过我们常常忽略,只有一个(3,2)本身是不能够精确表示一个向量的。我们仔细看一下,这里的3实际表示的是向量在x轴上的投影值是3,在y轴上的投影值是2。也就是说我们其实隐式引入了一个定义:以x轴和y轴上正方向长度为1的向量为标准。那么一个向量(3,2)实际是说在x轴投影为3而y轴的投影为2。注意投影是一个矢量,所以可以为负。
更正式的说,向量(x,y)实际上表示线性组合:
$x(1,0)^\mathsf{T}+y(0,1)^\mathsf{T}$
不难证明所有二维向量都可以表示为这样的线性组合。此处(1,0)和(0,1)叫做二维空间中的一组基。
所以,要准确描述向量,首先要确定一组基,然后给出在基所在的各个直线上的投影值,就可以了。只不过我们经常省略第一步,而默认以(1,0)和(0,1)为基。
基就是骨架,基的个数即为撑起给定维度空间的最小向量个数,通常设定基德模为1。
C-基变换的矩阵表示
但基不是唯一的,例如上一个例子中选(1,0)和(0,1)为基,同样,上面的基可以变为$(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$和$(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$。
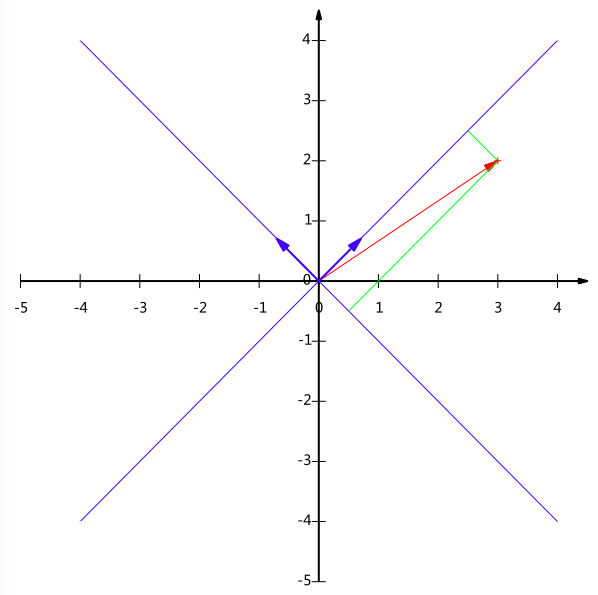
现在我们想获得(3,2)在新基上的坐标,即在两个方向上的投影矢量值,就需要利用到基变换的矩阵表示。
根据下图,我们只要分别计算(3,2)和两个基的内积,不难得到新的坐标为$(\frac{5}{\sqrt{2}},-\frac{1}{\sqrt{2}})$
同样我们可以利用基变换的矩阵表示进行求解:
再举一例:(1,1),(2,2),(3,3),想变换到刚才那组基上,则可以这样表示:
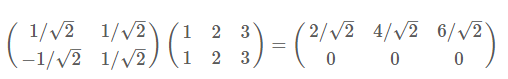
推广成一般性结论:
一般的,如果我们有M个N维向量,想将其变换为由R个N维向量表示的新空间中,那么首先将R个基按行组成矩阵A,然后将向量按列组成矩阵B,那么两矩阵的乘积AB就是变换结果,其中AB的第m列为A中第m列变换后的结果。
对应数学表达:
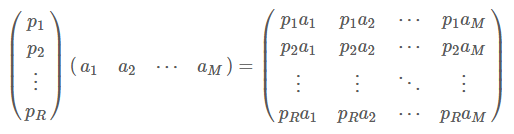
上述分析同时给矩阵相乘找到了一种物理解释:两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。这种操作便是降维。
D-最优基的选取方法
根据上面的分析,可以得出:只要找出合适的$p_1, p_2, …, p_R$,就可以实现对特征矩阵的投影,从而实现降维。为了便于分析,我们假设此处数据均已做中心化处理(去均值)。
对于未知的投影向量,我们假设投影变换表示为:
我们希望结果方差最大,即:
又对于投影向量,有$p_1p^T_1=1$,从而方差最大化可转化为含有拉格朗日乘子的函数:
为了简化书写,记:
求导并另导数为零,得出最优解:
将上式代入方差表达式,得到:
$var_1 = \lambda$
若要方差最大,只要特征值最大即可。由此可以观察:向量$p_1$即为$\Sigma$最大特征值所对应的特征向量。
同理,$p_2$为次大特征值对应的特征向量,依次类推,即可求得投影矩阵。
实际操作中,通常借助特征值分解(eig)或者奇异值分解(SVD)进行投影空间的构造。
(此处为补充内容,可跳过,不影响整体理解)换一种角度,通过奇异值分解的特性,也可以实现投影向量的理论推导:
而矩阵的能量为矩阵的迹:
从而方差的大小即为特征值的大小,从而根据特征值依次对应的特征向量,构造投影空间。
E-特征压缩
根据上面的推导,得到:
从而可以根据给定比例(如0.9)选定投影空间维度K(方式不唯一,此处仅仅给出参考)
假设投影矩阵为P,从而投影后的数据为:
三、算法步骤
- 步骤一:数据中心化——去均值,根据需要,有的需要归一化——Normalized;
- 步骤二:求解协方差矩阵;
- 步骤三:利用特征值分解/奇异值分解 求解特征值以及特征向量;
- 步骤四:利用特征向量构造投影矩阵;
- 步骤五:利用投影矩阵,得出降维的数据。
对应第一部分B-主成分分析 小节的成绩,结合算法步骤,给出MATLAB代码:
clc;clear all;close all;
set(0,'defaultfigurecolor','w') ;
x = [50 60 70 80 90];
y = [80 82 84 86 88];
figure()
subplot 121
scatter(x,y,'r*','linewidth',5);
xlim([50,100]);
ylim([50,100]);
grid on;
xlabel('语文成绩');
ylabel('数学成绩');
data = [x;y];
%步骤一:中心化
mu = mean(data,2);
data(1,:) = data(1,:)-mu(1);
data(2,:) = data(2,:)-mu(2);
%步骤二:求协方差矩阵
R = data*data';
%步骤三:求特征值、特征向量
%利用:特征值分解
[V,D] = eig(R);
[EigR,PosR] = sort(diag(D),'descend');
VecR = V(PosR,:);
%步骤四:利用特征向量构造投影矩阵
%假设降到一维
K = 1;
Proj = VecR(1:K,:);
%步骤五:利用投影矩阵,得出降维的数据
DataPCA = Proj*data;
x0 = -30:30;
subplot 122
scatter(data(1,:),data(2,:),'r*','linewidth',5);hold on;
plot(x0,Proj(2)/Proj(1)*x0,'b','linewidth',3);hold on;%绘出投影方向
xlim([-30,30]);
ylim([-30,30]);
grid on;
xlabel('语文成绩');
ylabel('数学成绩');
对应结果图,可以看出投影变换后新坐标轴的方向,即此时投影的间距最大,与上文分析一致:
对应完整的代码:
function y = pca(mixedsig)
%程序说明:y = pca(mixedsig),程序中mixedsig为 n*T 阶混合数据矩阵,n为信号个数,T为采样点数
% y为 m*T 阶主分量矩阵。
% n是维数,T是样本数。
if nargin == 0
error('You must supply the mixed data as input argument.');
end
if length(size(mixedsig))>2
error('Input data can not have more than two dimensions. ');
end
if any(any(isnan(mixedsig)))
error('Input data contains NaN''s.');
end
%——————————————去均值————————————
meanValue = mean(mixedsig')';
[m,n] = size(mixedsig);
%mixedsig = mixedsig - meanValue*ones(1,size(meanValue)); %当数据本身维数很大时容易出现Out of memory
for s = 1:m
for t = 1:n
mixedsig(s,t) = mixedsig(s,t) - meanValue(s);
end
end
[Dim,NumofSampl] = size(mixedsig);
oldDimension = Dim;
fprintf('Number of signals: %d\n',Dim);
fprintf('Number of samples: %d\n',NumofSampl);
fprintf('Calculate PCA...');
firstEig = 1;
lastEig = Dim;
covarianceMatrix = corrcoef(mixedsig'); %计算协方差矩阵
[E,D] = eig(covarianceMatrix); %计算协方差矩阵的特征值和特征向量
%———计算协方差矩阵的特征值大于阈值的个数lastEig———
%rankTolerance = 1;
%maxLastEig = sum(diag(D) >= rankTolerance);
%lastEig = maxLastEig;
lastEig = 10;
%——————————降序排列特征值——————————
eigenvalues = flipud(sort(diag(D)));
%—————————去掉较小的特征值——————————
if lastEig < oldDimension
lowerLimitValue = (eigenvalues(lastEig) + eigenvalues(lastEig + 1))/2;
else
lowerLimitValue = eigenvalues(oldDimension) - 1;
end
lowerColumns = diag(D) > lowerLimitValue;
%—————去掉较大的特征值(一般没有这一步)——————
if firstEig > 1
higherLimitValue = (eigenvalues(firstEig - 1) + eigenvalues(firstEig))/2;
else
higherLimitValue = eigenvalues(1) + 1;
end
higherColumns = diag(D) < higherLimitValue;
%—————————合并选择的特征值——————————
selectedColumns =lowerColumns & higherColumns;
%—————————输出处理的结果信息—————————
fprintf('Selected [%d] dimensions.\n',sum(selectedColumns));
fprintf('Smallest remaining (non-zero) eigenvalue[ %g ]\n',eigenvalues(lastEig));
fprintf('Largest remaining (non-zero) eigenvalue[ %g ]\n',eigenvalues(firstEig));
fprintf('Sum of removed eigenvalue[ %g ]\n',sum(diag(D) .* (~selectedColumns)));
%———————选择相应的特征值和特征向量———————
E = selcol(E,selectedColumns);
D = selcol(selcol(D,selectedColumns)',selectedColumns);
%——————————计算白化矩阵———————————
whiteningMatrix = inv(sqrt(D)) * E';
dewhiteningMatrix = E * sqrt(D);
%——————————提取主分量————————————
y = whiteningMatrix * mixedsig;
%——————————行选择子程序———————————
function newMatrix = selcol(oldMatrix,maskVector)
if size(maskVector,1)~= size(oldMatrix,2)
error('The mask vector and matrix are of uncompatible size.');
end
numTaken = 0;
for i = 1:size(maskVector,1)
if maskVector(i,1) == 1
takingMask(1,numTaken + 1) = i;
numTaken = numTaken + 1;
end
end
newMatrix = oldMatrix(:,takingMask);
四、应用实例
A-示例1:二维数据降维
以
为例,我们用PCA方法将这组二维数据其降到一维。
因为这个矩阵的每行已经是零均值,这里我们直接求协方差矩阵:
然后求其特征值和特征向量,具体求解方法不再详述,可以参考相关资料。求解后特征值为:
$\lambda_1=2,\lambda_2=2/5$
那么标准化后的特征向量为:
从而得到特征矩阵P:
最后我们用P的第一行乘以数据矩阵,就得到了降维后的表示:
降维投影结果如下图:
B-示例2:特征脸提取
例如文章:http://blog.csdn.net/mpbchina/article/details/7384425提到的特征脸提取(具体可参考原文):
附上一个人脸库链接:CroppedYale
为了小白可以理解,此处给一个简化版的MATLAB代码:
clc;clear all;close all;
set(0,'defaultfigurecolor',[0.2 0.3 0.5]) ;
FileDir = dir('*.jpg');
I = rgb2gray(imread(FileDir(1).name));
I = I(:);
result = zeros(length(I),length(FileDir));
figure(1)
for i=1:length(FileDir)
subplot (2,2,i);
I = rgb2gray(imread(FileDir(i).name));
imshow(I);
result(:,i) = I(:);
end
result = result';
%步骤一:去均值
for i=1:length(FileDir)
result(i,:) = result(i,:) -mean(result(i,:) );
end
%步骤二:协方差矩阵
CovRes = result*result';
%步骤三:求协方差矩阵
[U,S,V] = svd(CovRes);
%步骤四:求投影矩阵
%假设降至一维
K = 1;
ProjVec = U(1:K,:);
%步骤五:得到降维数据
PCAData = ProjVec*result;
ImgPCA = reshape(PCAData,size(I));
ImgPCA = ImgPCA - min(min(PCAData));
ImgPCA = ImgPCA/max(max(ImgPCA))*255;
figure();
imshow(uint8(ImgPCA));
C-示例3:葡萄酒案例
具体可参考:最后给出的链接,不再具体展开。
五、常见问题补充
(如果不配合准则函数-优化问题 ,PCA降维可不必对数据归一化,只做去均值处理即可。 这句话基本上是废话…)
- 数据特征的归一化,是对整个矩阵还是每一维特征?
整体做归一化相当于各向同性的缩放,这样处理起来没有作用;
各维分别作归一化会丢失各维方差这一信息,但各维之间的相关系数可以保留;
如果本来各维德量纲是相同的,最好不要做归一化,以尽可能多地保留信息;
如果本来各维的量纲是不同的,那么直接做PCA没有意义,就需要先对各维分别归一化。
- 为什么feature scaling 会使gradient descent 的收敛更好?
如果不归一化,各维度特征的跨度差距很大,目标函数就会是”扁“的:
(图中椭圆表示目标函数的等高线,两个坐标轴代表两个特征)
这样,在进行梯度下降的时候,梯度的方向就会偏离最小值的方向,走很多弯路。
如果归一化,那么目标函数就”圆 “了,从这里也可以明白:数据归一化,是针对每一个维度(特征)而言的,而不是整体。
看,每一步梯度的方向都基本指向最小值,可以大步前进。
以二维特征为例:
scaling避免了某个特征过大/小的问题。
- 常见特征(数据)归一化的方法?
- 最值归一化:比如把最大值归一化成1,最小值归一化成-1;或把最大值归一化成1,最小值归一化成0。适用于本来就分布在有限范围内的数据。
- 均值方差归一化:一般是把均值归一化成0,方差归一化成1。适用于分布没有明显边界的情况,受outlier影响也较小。
详细参考:http://blog.csdn.net/zbc1090549839/article/details/44103801
六、其他
- Karhunen-Loeve变换(KL变换):PCA为无监督类型,K-L变换则对有监督/无监督的场景都使用,且二者在原理上非常相似,如果有空闲,拟在后续文章进行讲解,此处不再展开;
- Kernel-PCA:核PCA (KPCA):PCA从方差角度进行论述,构造协方差矩阵,考虑的是线性关系,对于非线性关系没有进行讨论,Kernel可以将数据映射到高维。具体原理及应用本文不再详细整理。
参考:
今天的文章PCA算法分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/56125.html