什么是KMP算法？

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，简称KMP算法。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。

KMP算法与BF（暴力激活成功教程法）的区别

KMP算法是建立在BF算法基础上的，KMP算法与BF算法的最大区别在于，BF算法只能一位一位匹配，而KMP算法能够省去不必要的匹配步骤，从而实现跳位的匹配（具体如何跳位，看下图演示）。

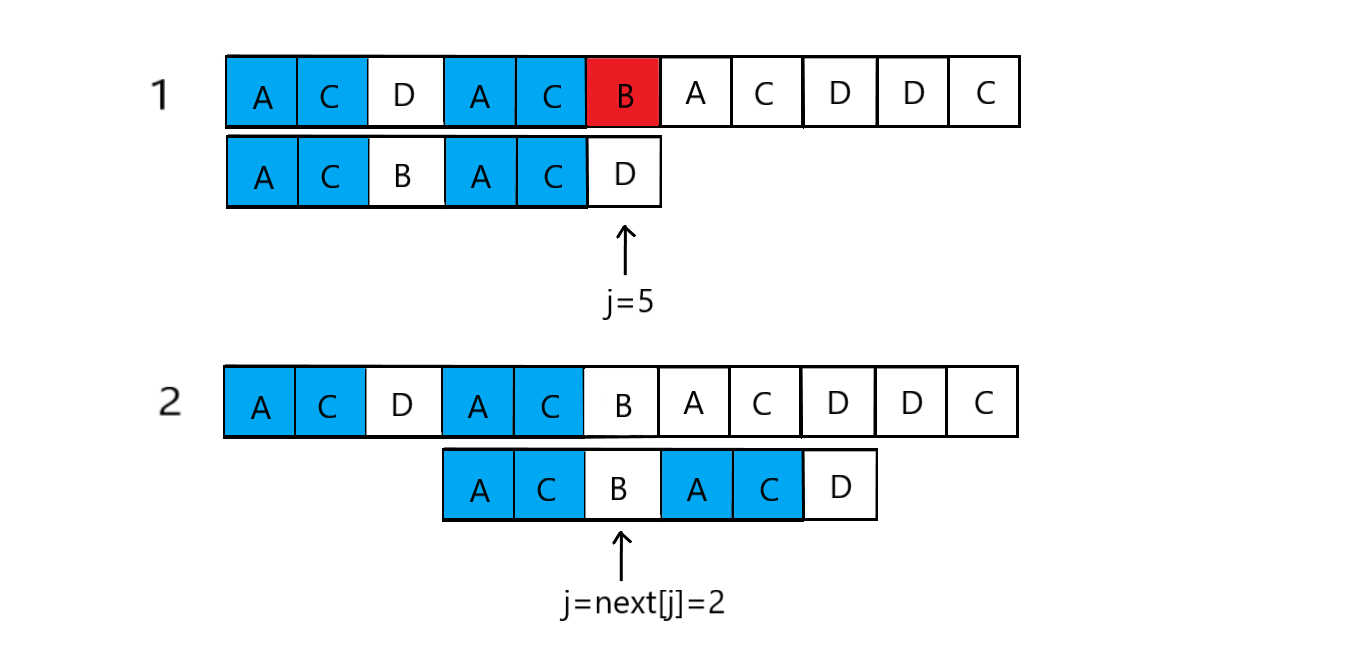
主串S“ACDACBACDDC”，模式串T“ACBACD”，匹配相比之下，BF算法匹配成功需匹配4次，而KMP算法只需匹配2次就可以，那么为什么KMP算法的步子可以跨这么大？是因为KMP算法中的next数组存放了模式串T出现重复字符的信息，利用已经部分匹配这个有效信息，保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置，而避免模式串移动到无效位置（BF算法中2-3步均为无效位置）。

通过算法比较我们发现KMP算法与BF算法结构类似，最大的区别在于else里的j=next[j]；也就是 i 不回溯，j 回溯到 next[ j ] 的位置，而不是每次都从零开始。
那么，看到这里，我们也就知道了KMP算法原理就是利用 j=next[j] 来回溯，来减少比较次数，或者是说跳过一些不必要的比较，也就是迈大步子。

next是啥？

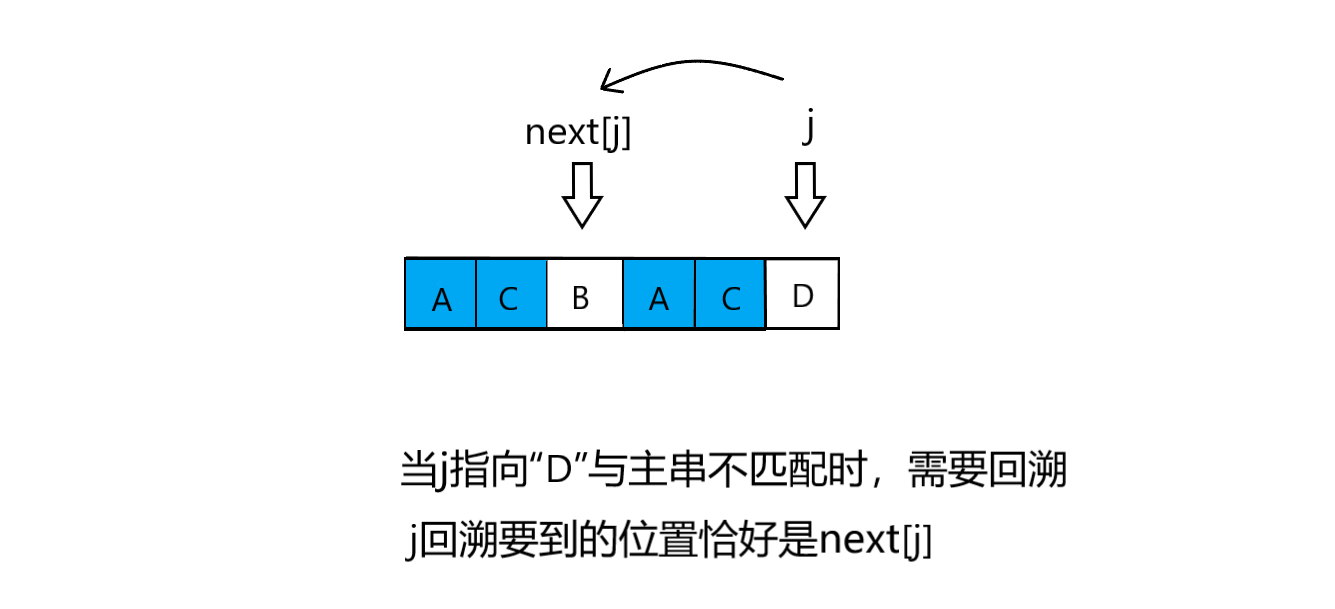
next顾名思义，是下一个的意思，那么其作用是在回溯时指引指针j回溯的下一位置，也就是j=next[j]；那么next[j]也就是j下一个要回溯到的位置。那么next数组就是用于存储每一位当发生不匹配时所对应的下一个要移动到的位置。言下之意next数组存的是位置（下标），通过带入j的值就可以获取到j的下一个回溯位置next[j]。
举个例子：主串S“ACDACBACDDC”，模式串T“ACBACD”（如下图），当前j=5时，模式串为“ACBACD”此时我们j位next[j]=next[5]=2，也就是说“D”前面（”D”的左边）最大匹配长度为2，我们观察模式串“ACBAC”也不难发现j指向的“D”的前面的“AC”（后缀）与模式串最前端的“AC”一致，那么在匹配的过程中（如下图所示），此时的指针j=5，所指的元素是“D”,然而“D”与主串中的”B”并不相等，那么，此时应该让j回溯，那么，回溯到什么位置呢？我们观察发现，“D”前面的AC先与主串匹配成功了，那么我们是不是只需要将，前缀的“AC”对齐，平移过来对齐，就可以了。

如何求next数组的值？

在模式匹配的过程中，模式串T中的每一位都可能发生失配的现象，失配就要进行回溯，那next[j]是如何知道模式串T的每一位要发生回溯时的下一位置？
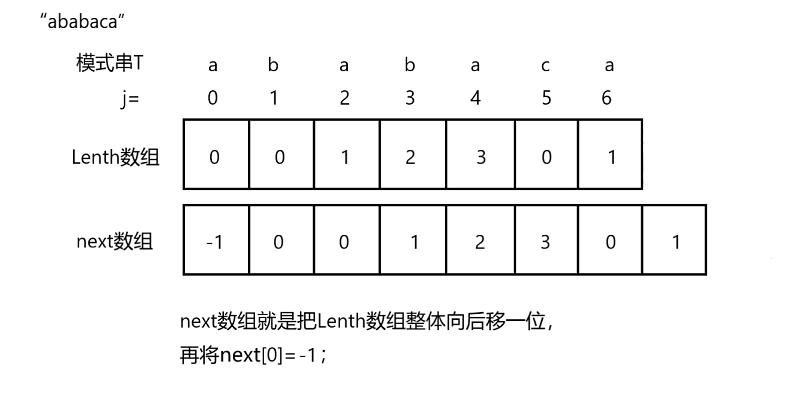
这个问题还得从 “最大长度”Length数组说起。“最大长度”Length数组是一个用来存放一个字符串的最长前缀和最长后缀相同的长度。按每一位对应的下标将对应长度值存于数组Length中，如模式串T为“ababaca”，长度是7，所以Length[0]，Length[1]，Length[2]，Length[3]，Length[4]，Length[5]，Length[6]分别计算的是 a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀的长度。所以Length[]={0,0,1,2,3,0,1};
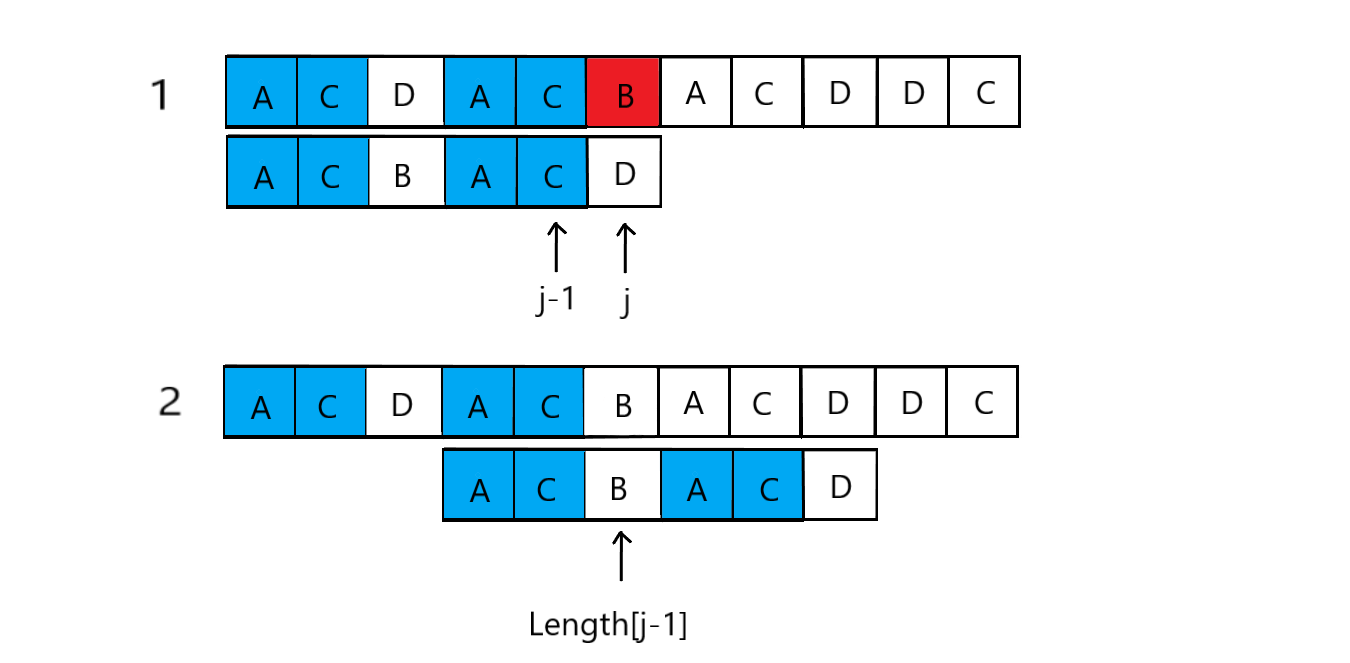
那我们的到了这个长度之后有什么用呢？Length数组的下标与模式串T的下标是一致的（也就是下标 j ），也就是模式串T中每一位都可以对应其下标（ j ）在Length数组中找到该位当前前缀与后缀的最长匹配长度，那么也就知道了，在当前位置下（也就是后缀）是否与模式串的开头（也就是前缀）有相同的部分、相同的部分是几位。那么我们举个例子当j=4时，此时模式串为“ababa”，那么此时显然有前缀：“aba”与后缀：“aba”相匹配，长度是3。那么我们将j=4带入Length[ j ];结果是Length[4]=3。那么此时，当j前走一位，j=5时，如果需要回溯，我们就可以知道回溯位置是Length[4]，也就是第四个位置。
那么也就是说，有了Length数组，我们只需要知道下标就可以知道，当前的前后缀的最长匹配长度。而当j位发生不匹配，需要回溯时，我们要看前一位也就是j-1位的前后缀匹配情况也就是Length[j-1]，可以知道要从j位回溯到Length[j-1]位。
那么现在问题来了，当我们发现j所指向的“D”此时发生失配的情况时，我们得去前一位 j-1（也就是Length[j-1]）找回溯位置，而并不能直接在Length[j]中找到，那么我们此时就引入next数组来代替Length数组来完成查找回溯位置这一工作。
所以next数组只需要在原有Length的基础上，整体向后移一位，即可实现通过next[j]直接找到j当前所需要回溯到的位置。

为什么要让next[0]=-1

未完待续

next数组有啥作用？

这就好比后缀中的“AC”是探路人，告诉后方是否能匹配，下一次回溯时，前缀中的”AC”就可以直接上前来，事实上不只是后缀“AC”，任何一个后缀都可以是探路人，这也就印证了为什么KMP算法的步子可以迈得大，因为有探路人探清楚了前面的情况，那后面的人就不需要小心翼翼的一步一步走，可以跨着走，跳着走。
那么现在我们就知道了，后缀这个探路人，在发现前方能匹配的情况下，通过next数组找到后人（与后缀最相匹配的前缀），让其上前来。如果next[ j ]=0的话，那说明没有后人（不存在与后缀最相匹配的前缀），那只能重头开始。
next数组也正是KMP算法的精髓所在，充分记录并利用探路人（后缀）获取的信息（已匹配信息），让算法能绕过很多不必要的匹配项，少走很多弯路。

如何让程序求出next数组？

从代码比较来看我们会发现求next数组的函数和KMP算法的结构惊人的相似，那么其实求next数组就是让模式串T的前缀和后缀相匹配，那么也就是一个自我匹配的过程，用前缀去匹配后缀。
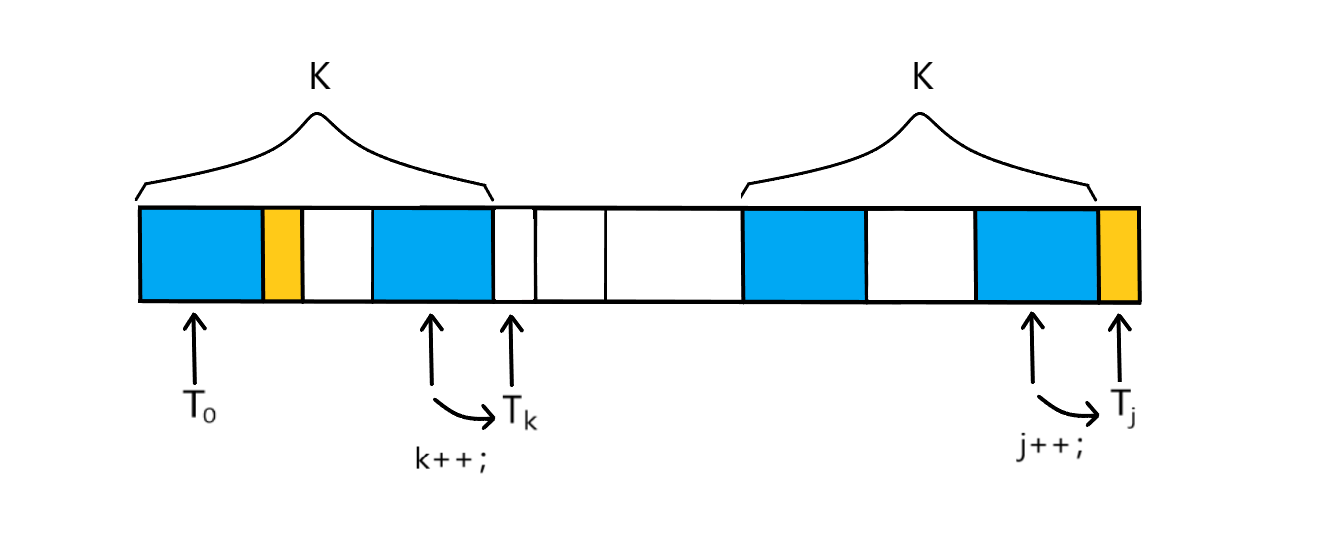
那么不同之处在于当匹配成功时，我们不但要把指针（下标）向后推一位，还同时需要对应当前下标记录下当前的最佳匹配长度，也就是next[j]=k；k表示的是模式串T的前k项与后k项相匹配（如下图），那么k也正是当前的匹配长度，那么我们将这个长度记录在next数组的第j位也即是next[j]=k;那么我们也就完成了当第j位时，将前缀与后缀的最佳匹配长度k存储于next[j]中。
那么此处你可能会有疑问了，求next数组不是得先求出Length吗？我们知道next数组是在Length数组上下标+1，那么我们注意看if中的代码，j在判断完T[j]==T[k]；之后j++；k++；那么这个j此时已经向后推了一位，k也想后推了一位，那么此时的k的值也就是前k位的长度值（长度为k，数组下标是0~k-1，所以坐标得加1才是长度值），然后在执行next[j]=k；将k记录于next[j]；那么这个先后顺序，就成功的将匹配信息记录于next数组中。

f(k==-1||T[j]==T[k])
		{ 
   
			j++;//注意执行顺序，先j++，k++，再next[j]=k；
			k++;
			next[j]=k;
		}

当匹配失败时，我们可以看到KMP算法和求next数组的算法，处理方式是一样的，都是将当前指针回溯也就是k=next[k]；
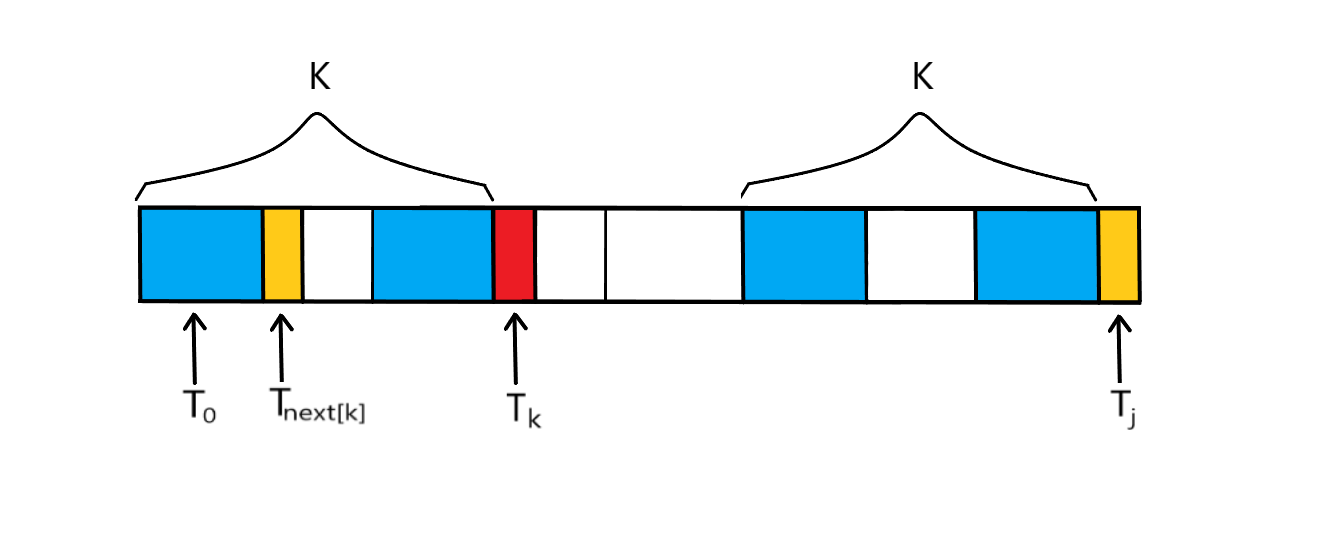
很多人理解不了next函数中的k=next[k]；其实在此处（如下图）相当于是将模式串T分割成两半，让前缀去和后缀相匹配，那么我们此时可以确定的是前k项（前缀）与后k项（后缀）成功匹配，那么此时做的是看一下在这个基础上能不能找到更长的匹配长度也就是前k+1项（新的前缀），和后k+1项（新的后缀）相匹配，如果可以，记录k+1于next数值，接着看再k+1的基础上能否有k+2的前后缀最匹配长度…
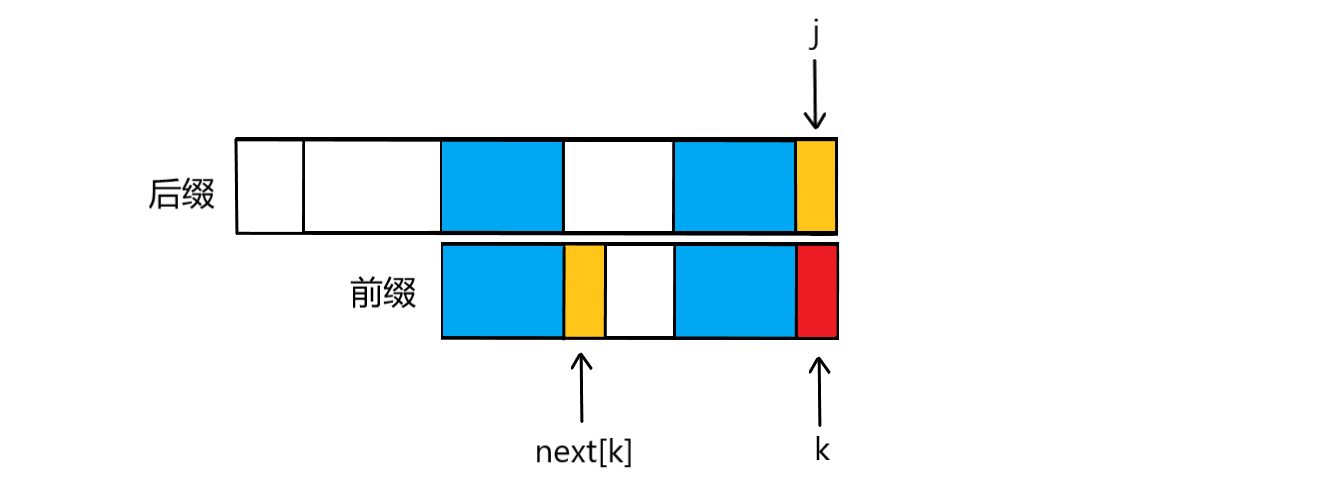
那如果在前k项与后k项相同的情况下，第k+1项失配，也就是下图所视情况，T[k]≠T[j] ，那么我们的前缀指针k是不是要回溯，在此处使用BF算法的回溯思路，从零开始重新找前后缀匹配长度，固然可以，但是我们如果用kmp算法的回溯思路，是不是可以更快找到呢？
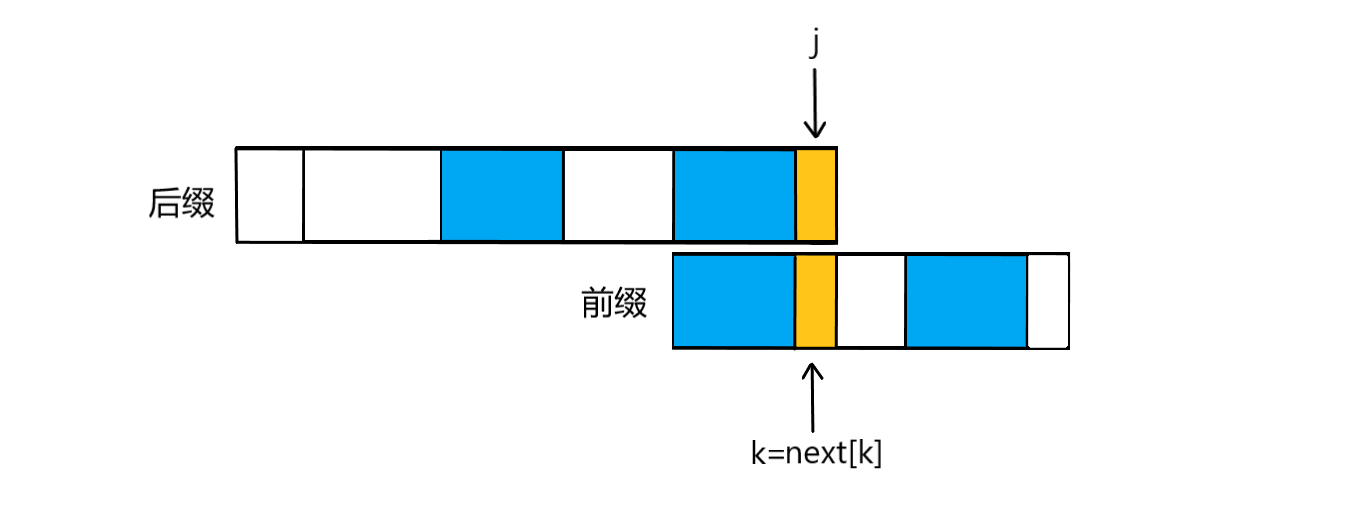
如图示，根据next数组的存放值的含义我们通过next[k]可以知道，T[k]前是否有已匹配项，根据图示，我们可以发现蓝色部分是已匹配项，那么此时我们是不是只用取比较T[ next[k] ] 与T[ j ] 的值是否相等即可？那么也就是k=next[k]；
那么看到这里，你可能又会有疑问了，这个GetNext函数不是在求next数组吗？那我的next数组都还没有求完，你又怎么可以用next数组去求下一回溯位置呢？
那么其实，我们回去看看设定，会发现k是永远比j小的，此时模式串已经处理到第j位，对应的next数组也对应的填到了next[j]的位置，那么也就是说next[0]~next[j]都是可用的，而0<k<j，那么k=next[k]；自然是没问题的。
说到这里我们也就豁然开朗了，其实BF算法,KMP算法，求next数组的算法，这三者结构都是十分相似的，因为本质上都是模式匹配，只不过后两者在回溯上有更聪明的回溯方法罢了。

升级版next数组
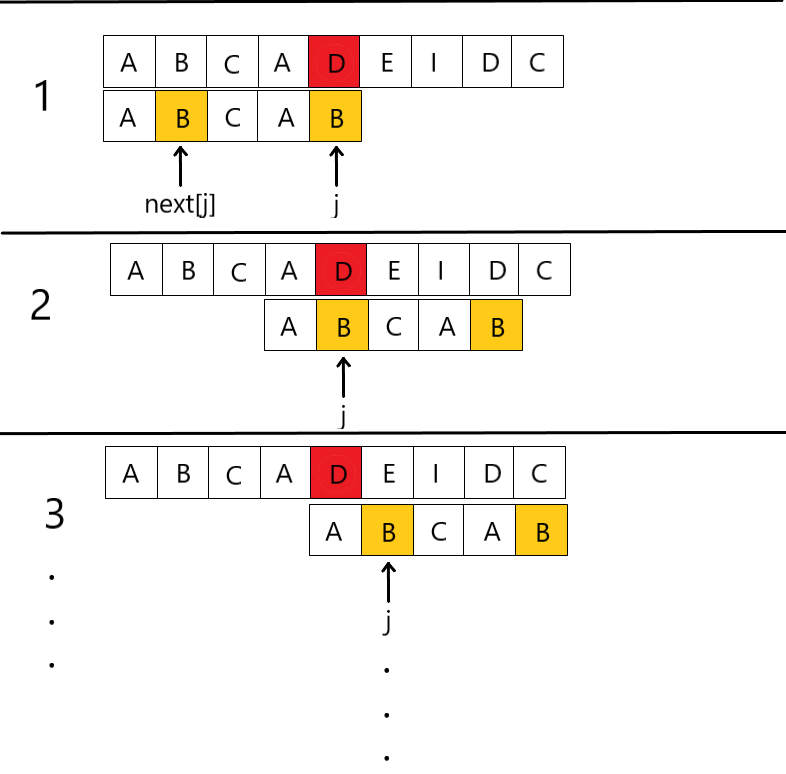
我们发现这个算法其实还是存在漏洞，如下图的情况，第2步的情况是完全没有必要的，因为在第1步时已经判断过“B”≠”D”,第2步又判断了一次“B”≠”D”。那有没有办法可以省掉，或者是跳过这个多余步骤呢？

其实我们只需要加一个判断就可以了，当if(k==-1||T[j]==T[k])判断完前k项与后k项相匹配后，j++；k++；此时j和k都向后推了一位，分别指向下一位，那么这时我们不着急记录长度k于next数组，而是加一个判断，预判断一下下一位（这里的下一位是指j++；k++；之前的下一位）是否相等，也就是T[j]与T[k]是否相等，如果不相等，我们记录k的值于next数组；如果相等的话，就会出现上述多余重复匹配的现象，那么我们在这里通过连续的两次回溯，来跳过它，也就是k = next[next[k]]；（next[j]=next[k]；将next[k]的值存于next[j]也是一样的道理），回溯完之后不进行匹配判断就进行下一次回溯，即是跳过了他的匹配步骤。

void Nextval(char T[],int *next)
{ 
   
	int lenT=strlen(T);
	int k=-1;//前缀 
	int j=0;//后缀 
	next[0]=-1; 
	
	while(j<lenT)
	{ 
   
		if(k==-1||T[j]==T[k])
		{ 
   
			j++;
			k++;
			//较之前next数组求法，改动在下面4行
			if(T[j]!=T[k])
			{ 
   
				next[j]=k;//之前只有这一行
			}
			else
			{ 
   
				next[j]=next[k];/*为不能出现T[j] = T[ next[j ]]， 所以当出现时连续进行两次回溯，k = next[next[k]] */ 
			 } 
		}
		else 
		{ 
   
			k=next[k];
		 } 
	}
}

其他问题

看到这里你可能会想到，kmp算法是通过记录模式串T中的重复数据信息，来达到跳步，那么如果模式串T中没有相匹配的前后缀呢？如：“ABCDEF”那kmp算法还能发挥作用吗？

如果模式串T中完全没有相匹配的前后缀，那么 此时KMP算法的效能将发挥到极致！每次都可以实现最大量化的移动距离。

待补充…

完整版代码

#include <stdio.h>
#include <string.h>
#define maxsize 100 

void Nextval(char T[],int *next)
{ 
   
	int lenT=strlen(T);
	int k=-1;//前缀 
	int j=0;//后缀 
	next[0]=-1; 
	
	while(j<lenT)
	{ 
   
		if(k==-1||T[j]==T[k])
		{ 
   
			j++;
			k++;
			//较之前next数组求法，改动在下面4行
			if(T[j]!=T[k])
			{ 
   
				next[j]=k;//之前只有这一行
			}
			else
			{ 
   
				next[j]=next[k];/*为不能出现T[j] = T[ next[j ]]， 所以当出现时连续进行两次回溯，k = next[next[k]] */ 
			 } 
		}
		else 
		{ 
   
			k=next[k];
		 } 
	}
}

int KMP(char S[],char T[])
{ 
   
	int i=0,j=0,lenS,lenT;
	lenS=strlen(S);
	lenT=strlen(T);
	
	int next[maxsize];
	Nextval(T,next);
	
	while(i<lenS&&j<lenT)
	{ 
   
		if(j==-1||S[i]==T[j])
		{ 
   
			i++;
			j++;
		}
		else
		{ 
    
			j=next[j];
		}
	}
	 
	if(j==lenT)
	{ 
      
	    printf("Match succeed!\n");
	 	return i-j;
	} 
	else 
	{ 
   
		printf("Match failed!\n");
		return -1;
    }
}


int main() 
{ 
   
    char S[maxsize],T[maxsize];
    int target;
	
	strcpy(S,"AAAAAAAAAAttract");
	strcpy(T,"Attract");

	target=KMP(S,T);
	printf("Position is %d\n",target);
	return 0;
}

聊聊模式匹配算法

模式匹配算法除了我们提到的BF,KMP还有效率更高的BM,Sunday算法，KMP算法在BF一步一步走的基础上，实现了跨步跳步，将时间复杂度从O（m*n）降到了O（m+n），但是跨步的距离还是有局限性的，跨步的距离取决于模式串T的长度，模式串长度越长，那么可能实现的跨步距离也越大，那么Sunday算法其实就是打破了这一局限性，不需要取决于模式串得长度来查找匹配，从而也能将算法效能突破新的高度。

参考：

从头到尾彻底理解
详解KMP算法
部分文图来自于：懒猫老师
《数据结构第二版》，严蔚敏 & 吴伟民编著；

今天的文章kmp算法c++实现_朴素匹配算法分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/58077.html

kmp算法c++实现_朴素匹配算法