python中求矩阵的逆_矩阵的转置和矩阵的逆「建议收藏」

我就废话不多说了，大家还是直接看代码吧~

import numpy as np

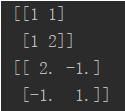
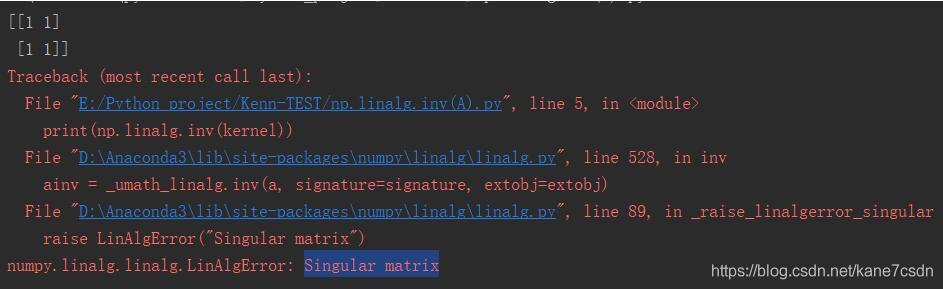
kernel = np.array([1, 1, 1, 2]).reshape((2, 2))

print(kernel)

print(np.linalg.inv(kernel))

注意，Singular matrix奇异矩阵不可求逆

补充：python+numpy中矩阵的逆和伪逆的区别

定义：

对于矩阵A，如果存在一个矩阵B，使得AB=BA=E，其中E为与A,B同维数的单位阵，就称A为可逆矩阵(或者称A可逆)，并称B是A的逆矩阵，简称逆阵。(此时的逆称为凯利逆)

矩阵A可逆的充分必要条件是|A|≠0。

伪逆矩阵是逆矩阵的广义形式。由于奇异矩阵或非方阵的矩阵不存在逆矩阵，但可以用函数pinv(A)求其伪逆矩阵。

基本语法为X=pinv(A),X=pinv(A,tol),其中tol为误差,pinv为pseudo-inverse的缩写：max(size(A))*norm(A)*eps。