HDU – 7049 – Link with Grenade ( 物理 + 数学 )

题目链接：点击进入

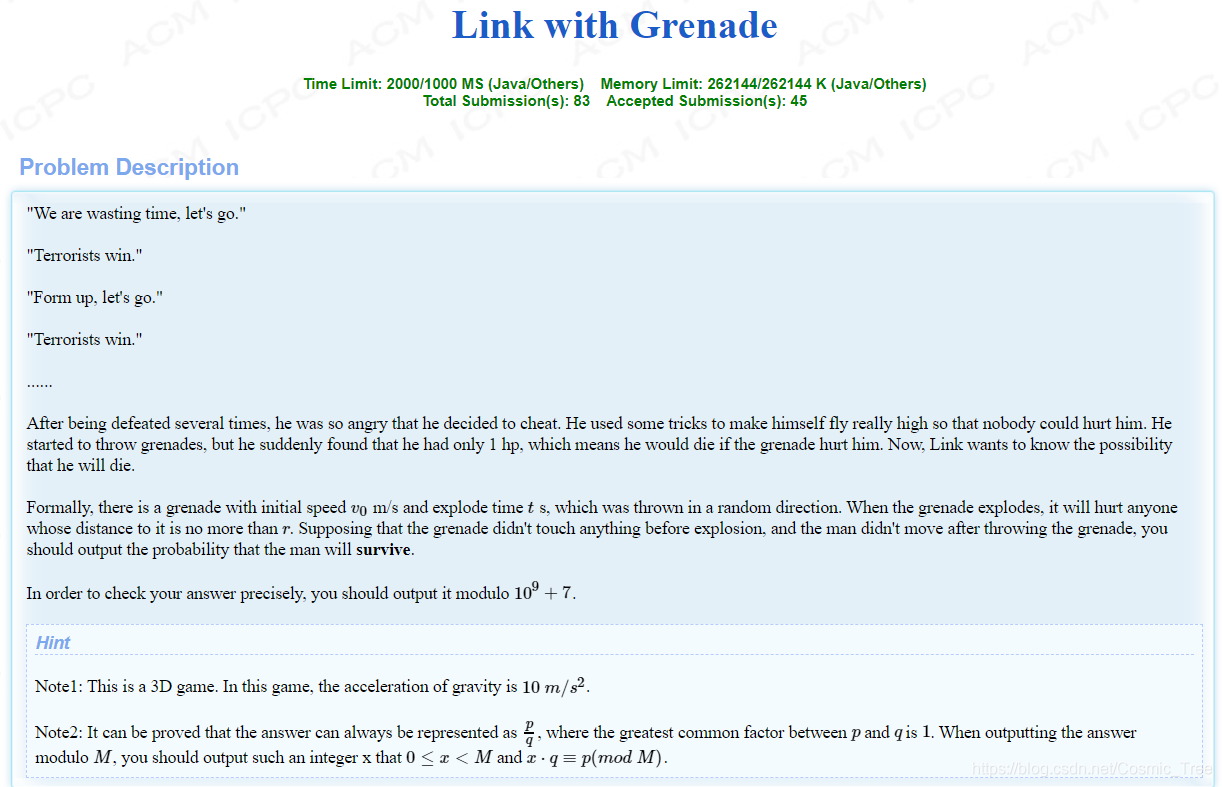
题目

题意

你站在一个很高很高很高的地方，你手里有颗手榴弹，随便选一个方向，以初速度 v0 扔出去，t0 秒后爆炸，考虑重力加速度 $10m/s^2$，手榴弹爆炸范围为半径为 R 的球，人要是在这个范围内必死，问人不死的概率。

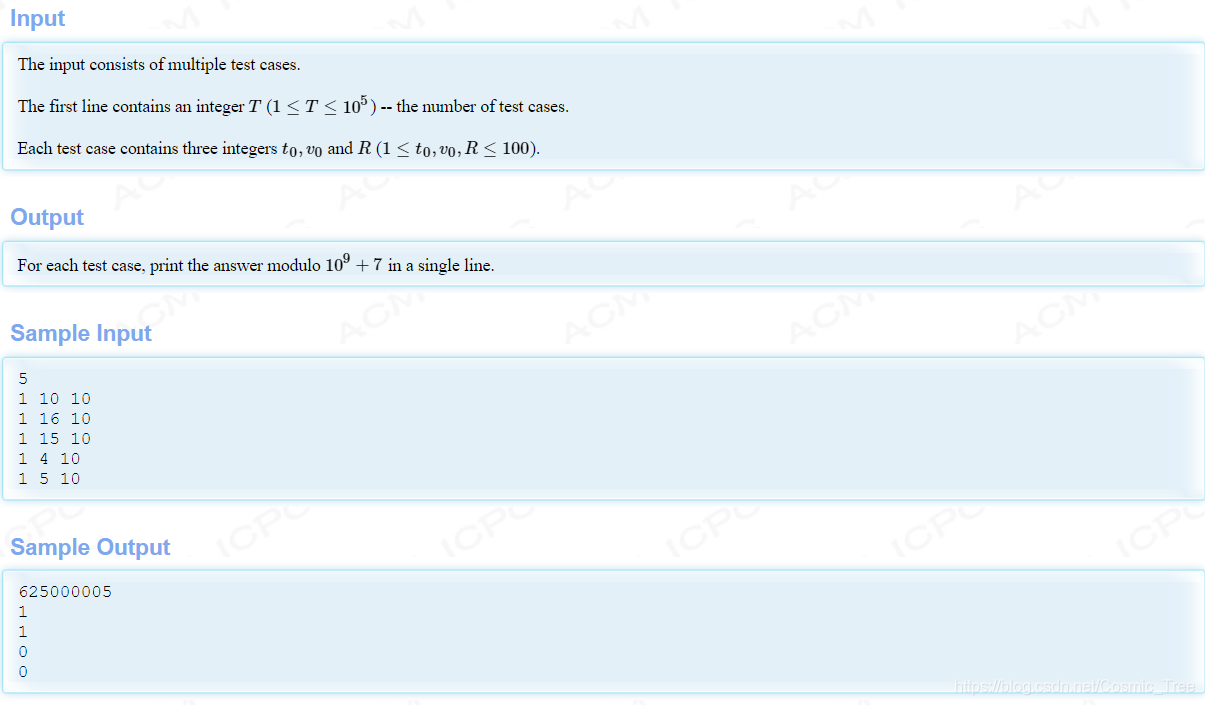
思路

大概想一下，人站在原点，固定一个起手的角度，然后原地转圈360°扔炸弹，得到的结果是一样的，炸弹的落脚点离人的距离都是一样的，那么我们实际上就可以只看一个经过人的竖直面就可以了。
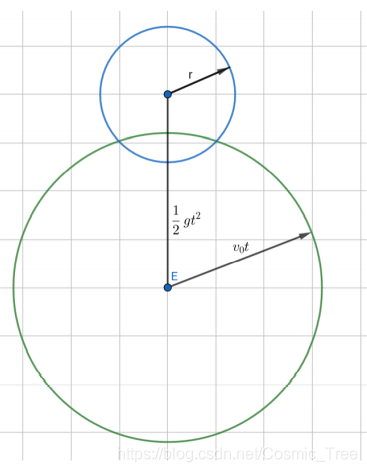
题目说人不动，炸弹具有重力加速度，但是这个扔出去的炸弹落脚点的轨迹不好判断。考虑给整个图加上个向上的值为 10 的加速度，抵消重力加速度。那么炸弹就相当于做匀速直线运动，人做初速度为 0 的匀加速直线运动。t0 秒后，人的位置为原点上方的$\frac{gt{0}^2}{2}$处，炸弹向各个方向扔 ( 竖直平面上 ) ，落脚点轨迹是个半径为 v0 * t0 的圆。配个官方题解的图：

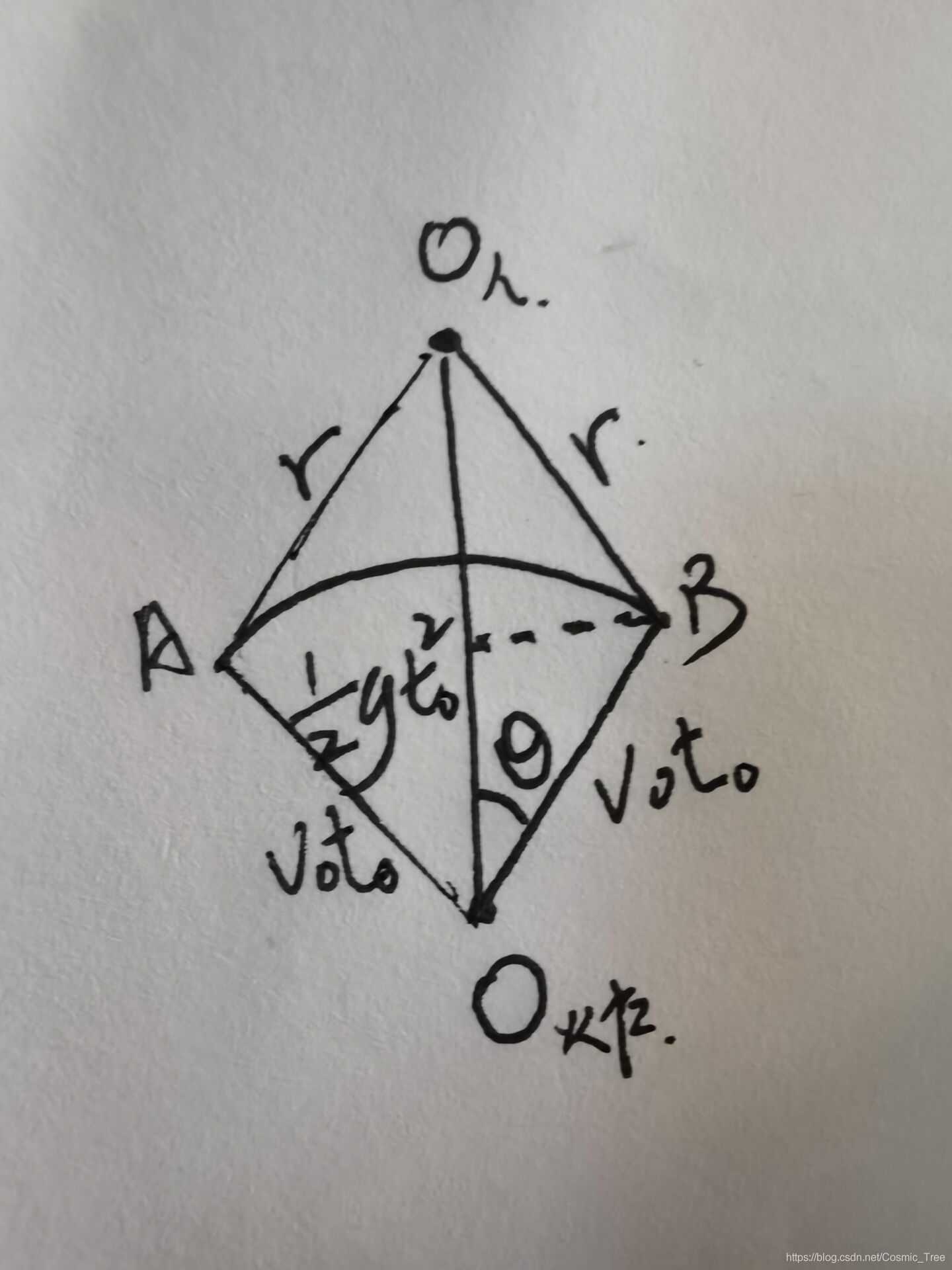
接下来就是判断炸弹轨迹与人位置距离小于等于 r 的地方都是哪些了。如下：

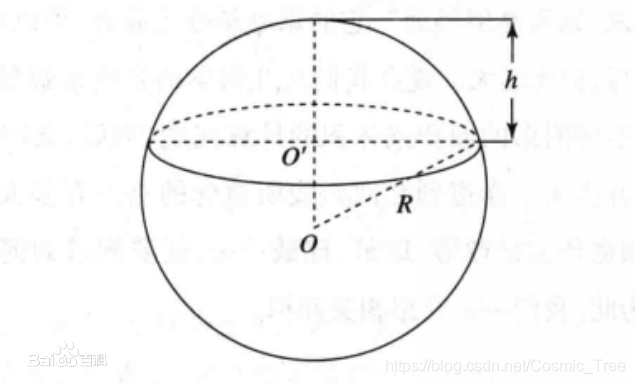
由上图我们知道，弧AB的地方就是人可以被炸弹炸到的地方。那拓展到球面上，就是一个球冠表面积。已知：

假设球面的半径是 R ，球冠的高是 h ，那么球冠的表面积公式为：$S=2\pi Rh$
带入得，可以炸到人的球面面积为 $2\pi (v0t0{)}^2(1-cos\theta )$ ，球的表面积为 $4\pi (v0t0{)}^2$，因此被炸到的概率为 $\frac{1-cos\theta }{2}$ ，那么活下来的概率为 $\frac{1+cos\theta }{2}$ ，又因余弦定理 $cos\theta$ 可求，带入得：

判断一下特殊情况，否则就是 $\frac{p}{q}$ ( 记得逆元 )

代码

//#pragma GCC optimize(3)//O3
//#pragma GCC optimize(2)//O2
#include<iostream>
#include<string>
#include<map>
#include<set>
//#include<unordered_map>
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<stack>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<fstream>
#define X first
#define Y second
#define best 131 
#define INF 0x3f3f3f3f3f3f3f3f
#define pii pair<int,int>
#define lowbit(x) x & -x
#define inf 0x3f3f3f3f
#define int long long
//#define double long double
//#define rep(i,x,y) for(register int i = x; i <= y;++i)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double pai=acos(-1.0);
const int maxn=1e6+10;
const int mod=1e9+7;
const double eps=1e-9;
const int N=5e3+10;
/*--------------------------------------------*/
inline int read()
{ 
   
    int k = 0, f = 1 ;
    char c = getchar() ;
    while(!isdigit(c)){ 
   if(c == '-') f = -1 ;c = getchar() ;}
    while(isdigit(c)) k = (k << 1) + (k << 3) + c - 48 ,c = getchar() ;
    return k * f ;
}
/*--------------------------------------------*/

int t,v0,t0,r;
int qpow(int a,int b)
{ 
   
    int res=1;
    while(b)
    { 
   
        if(b&1) res=res*a%mod;
        a=a*a%mod;
        b=b>>1;
    }
    return res;
}

signed main() 
{ 
   
// ios::sync_with_stdio(false);
// cin.tie(0);cout.tie(0);
    cin>>t;
    while(t--)
    { 
   
        cin>>t0>>v0>>r;
        int p=4*10*v0*t0*t0*t0+10*10*t0*t0*t0*t0+4*v0*v0*t0*t0-4*r*r;
        int q=8*10*v0*t0*t0*t0;
        if(p<=0) cout<<0<<endl;
        else if(p>=q) cout<<1<<endl;
        else
        { 
   
            int ans=p*qpow(q,mod-2)%mod;
            cout<<ans<<endl;
        }
    }
    return 0;
} 

今天的文章HDU – 7049 – Link with Grenade ( 物理 + 数学 )分享到此就结束了，感谢您的阅读。