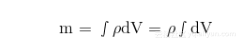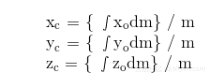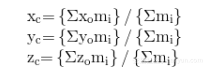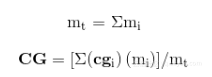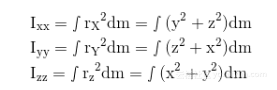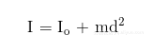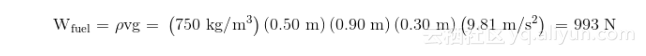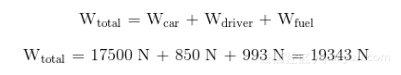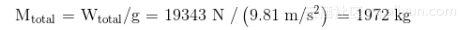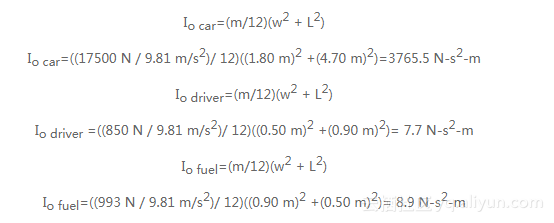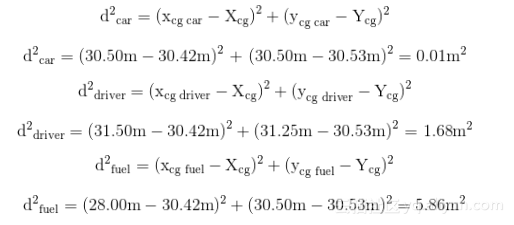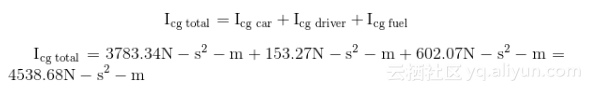《游戏开发物理学（第2版）》一1.6　质量、质心和转动惯量

本节书摘来异步社区《游戏开发物理学（第2版）》一书中的第1章，第1.6节，作者： 【美】David M Bourg , Bryan Bywalec 译者： 崔力强 , 魏广程 责编： 陈冀康，更多章节内容可以访问云栖社区“异步社区”公众号查看。

1.6　质量、质心和转动惯量

物体的属性——质量（mass）、质心（center of mass）和转动惯量（moment of inertia），总体来讲被称为质量特性（mass properties）——对于研究力学来说是至关重要的，因为物体的线性运动、角运动及物体对于给定外力的响应都是质量特性的函数。因此，为了准确建模物体的运动，你需要知道或者有能力计算这些质量特性。让我们先看几个定义。

通常来讲，人们认为质量是用来衡量一个物体中含有物质的多少。从研究力学的角度来讲，也可以认为质量是用来衡量物体对于运动或者运动中的变化的阻力。因此物体的质量越大，就越难让它动起来，或者说越难改变它的运动状态。

在力学以外的术语中，质心（也被称为重心（center of gravity））是物体上的一个点，该物体的质量均匀的分布在质心的周围。在力学中，质心是这样一个点，当任何的外力施加在该点上的时候，都不会引起该物体的转动。

虽然大多数人熟悉质量（mass）和重心（center of gravity）这样的术语，但是转动惯量就没有那么熟悉了；然而在力学中，它们都是一样重要的。一个物体的转动惯量是当物体在一个坐标轴上的转动的时候，用来衡量该物体质量的放射性分布指标。质量是物体对于线性运动的阻力[1]，类比之下，可以认为转动惯量是用来衡量物体对转动的阻力的。

现在你已经知道这些属性是什么意思了，我们来看看如何计算它们。

对于由多部分组成的物体，总质量可以通过简单地把每个部分的质量加起来得到。每个部分的质量可以通过密度乘以体积得到。假设该物体的密度是统一的，那么该物体的总质量就可以简单地用密度乘以物体的总体积得到。这个可以使用下面的方程表示：

在实践中，你通常不需要做体积的积分来得到物体的质量，尤其是我们将要考虑的那些物体（例如汽车和飞机）的密度并不是均匀的。因此你可以把物体分解成为比较容易计算质量的部分，计算每个部分的质量，然后简单地把每个部分的质量加起来，从而得到总质量。

物体重心的计算更复杂点。首先，把物体分为有限个基本的质块，每个质块的中心使用参考坐标系的轴来定位，使用mi来引用这些质块。接下来取每个质块的相对于参考坐标轴的一阶距（first moment），再把它们加起来。一阶距求解方法如下：先得到沿着某个给定的坐标轴从原点到质块中心的距离，该距离与该质块质量的乘积即为一阶距。最后把所有质块的一阶距的和除以物体总质量，就可以得到该坐标轴上的物体质心的坐标。你必须对每个维度都做这样的计算，也就是说，对2D做两次计算，对3D做三次计算。下面是物体质心3D坐标的方程。

其中（x，y，z）c是物体质心的坐标，而（x，y，z）o是每个质块的质心坐标。量xodm、yodm和zodm表示质块质量dm关于坐标轴的一阶距。

这里，不用太担心这些积分方程。在实践中你只需将有限的质量相加，方程看起来会友好很多，如下所示：

注意，你可以轻易地将这些方程中的质量替换为重量，因为重力加速度g会同时出现在分子和分母中，因此会从等式中消去。记住，物体的重量就是它的质量乘以重力加速度g，g在海平面为9.8 m/s2。

计算物体总质量和离散粒子系统重心的方程可以很方便地写作向量符号形式如下：

其中mt是总质量，mi是每个系统中每个粒子的质量，CG是合并后的重心，而cgi是每个粒子在设计或参考坐标下的重心。注意CG和cgi是向量，因为它们表示笛卡尔坐标系中的位置。这样做是为了方便你能够一次处理x、y、和z（或者在二维中的x和y）。

在稍后的示例代码中，让我们假设组成物体的粒子由一种数据结构组成的数组表示，每个这种数据结构都包含对应点粒子的设计坐标和质量。这个数据结构同样会包含稍后计算的粒子相对于组合后刚体质心的坐标。

这里是示范如何计算总质量以及合并元素重心的代码：

现在解出了合并后的重心位置，你就可以计算每个粒子的相对位置如下：

为了计算转动惯量，你需要取组成物体的每个粒子对于每条坐标轴的二阶矩。之后用所得二阶矩乘以质量与距离平方的积。这个距离不是沿计算质心时的坐标轴到粒子中心的距离，而是从我们计算转动惯量相对的坐标到粒子中心的垂直距离。

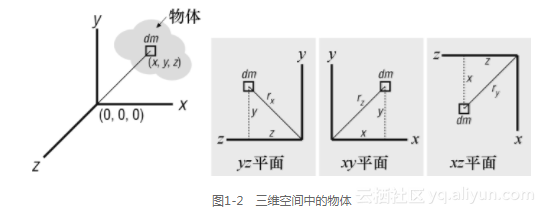
三维中的任意物体如图1-2所示，当计算对于x轴的转动惯量Ixx时，距离rx将会在yz平面上，rx2=y2+z2。同样的，对于关于y轴的转动惯量 Iyy，r y2 = y2 + z2，而对于关于z轴的转动惯量Izz，r z2 = y2 + z2。

三维中相对于坐标轴的转动惯量方程为：

让我们看一眼实际中矩的更通常的情况。假设给定物体对于穿过物体质心的中性轴（neutral axis）的转动惯量为Io，而你想知道对于平行与这个中性轴但有一定距离的另一个轴的转动惯量I，你可以使用坐标变换，或者平行轴定理（parallel axis theorem）来确定对于这个新轴的转动惯量。需要使用的公式如下：

其中m是物体的质量，而d是两轴之间的垂直距离。

这里有一个重要的实用观测：新的转动惯量是两坐标轴分开距离平方的函数。这表明当Io比较小而d比较大时，你可以安全地忽略Io，因为md2项将占主导地位。当然，在这里你需要尽力判断。这个用于变换坐标轴的公式同时表明了物体的转动惯量在相对于过物体重心的轴计算时最小。物体对于任何不通过物体质心的平行轴的转动惯量将会增大md2。

在实践中，除了对密度均匀的简单形状，计算转动惯量都是一个很复杂费力的过程，因此我们通常会将物体对于一个过其质心的转动惯量使用近似物体的基础形状的公式来进行近似求解。进一步，我们会将复杂物体分成小组件，并利用某些组件的Io相对于其md2对于整个物体转动惯量的可以忽略的特性简化计算。

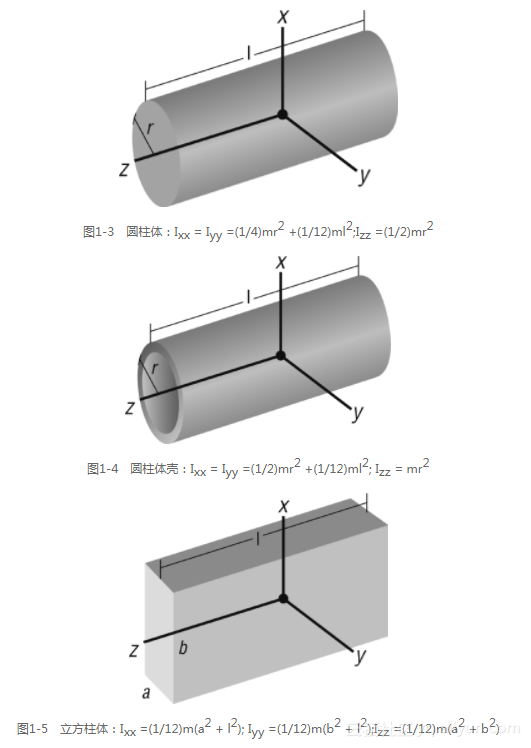
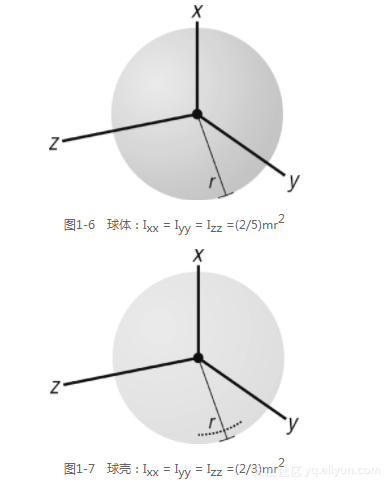
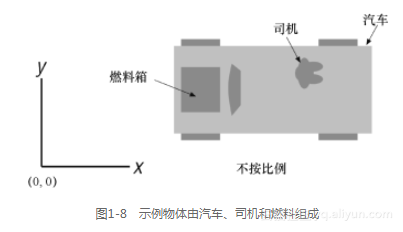
图1-3到图1-7展示了一些能够轻松地计算转动惯量的简单几何实体。在图题中展示了这些简单密度均匀的几何体相对于三个坐标轴的转动惯量公式。你可以轻易地在大学动力学教材中找到其他基础几何体的类似公式。

正如你所见到的，这些公式实现起来相对简单。这里用到的技巧就是将一个复杂物体分为一系列小而简单的有代表性的几何形，它们组合起来会近似于复杂物体的惯性属性。这个联系很大程度上是一种考虑期望精度水平的判断。

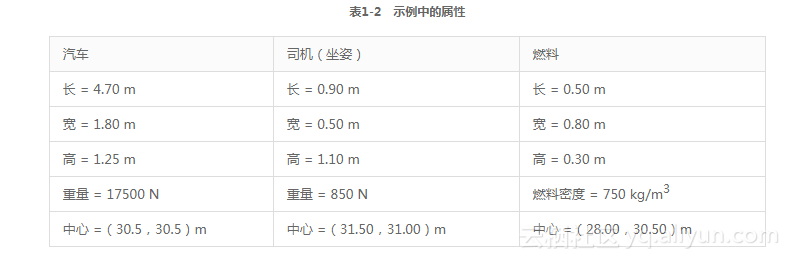
让我们通过一个简单的2D示例来展示如何应用本节中讨论过的公式。假设你正在编写一个自顶向下视图的自动赛车游戏，想在其中使用基于2D刚体动力学仿真汽车精灵。在游戏最开始，玩家的汽车处于起跑线，加满油并准备出发。在开始仿真之前，你需要计算初始状态时车、司机和燃料载重的质量特性。在这个例子中，物体（body）由三部分组成：车、司机和满载的燃料。之后在游戏中，物体的质量会随着燃料燃烧和司机在车祸中被甩出去变化。现在，让我们只注意图1-8所示的初始状态。

示例中每个组件的属性在表1-2中给出。注意，长延x轴测量，宽延y轴，高会向外伸出屏幕。同时注意每个组件中心坐标，即写作（x，y）形式是在全局坐标系下书写的。

我们需要计算的第一个质量特性是物体的质量。由于我们已经有了汽车和司机的重量，这个计算就很简单了。余下的燃料重量就是我们所谓唯一缺少重量分量。由于我们有了燃料的密度和油箱形状，我们可以计算出油箱体积并乘以密度和重力加速度来得到油箱中燃料的重量。得出燃料为920.6N，如下：

重力加速度（Acceleration due to gravity）是正在下落的物体向地面掉落时的加速度。一个物体的重量等于它的质量乘以重力加速度。符号g用于表示重力加速度，g在地球海平面高度的值大约是9.8 m/s2 。重量在公制系统中的单位是牛顿N。
现在，物体的总重量为：

为了得到物体的质量，你只要简单地将重量除以重力加速度。

我们需要的下一个质量特性是物体的重心位置。在这个示例中我们将会计算相对于全局坐标系原点的物体中心坐标。我们同样会将一阶矩公式应用两次，一次对于x坐标，另一次对于y坐标：

注意，我们在这些公式中使用了重量而非质量。记住，由于重量中的重力加速度是个常量，并且同时出现在分子、分母中而被消去，所以我们可以这么做。

现在到了计算物体转动惯量的时候了。在这个2D示例中计算过程足够简单，因为我们只有一个转动轴指向纸张外，因此我们只需要进行一次计算。第一步是计算每个组件相对于自己中性轴的局部转动惯量。由于我们对于每个组件几何形和质量分布信息了解是有限的，我们将会进行一个简化的近似，通过将每个组件表示为一个方柱体，因此可以应用图1-5中相应的转动惯量公式。在下列等式中，我们将会用小写的w表示宽度，以便不与它的重量混淆，我们之前用大写的W表示重量。

由于这些结果是每个组件关于它自己中性轴的转动惯量，我们现在需要用平行轴定理将这些矩转换成相对于过我们刚计算得出的物体重心的中性轴的转动惯量。

为了进行这个计算，我们必须解出从物体重心到每个组件重心的距离。从每个组件重心到物体重心的距离平方为：

现在我们可以应用平行轴定理如下：

注意计算司机和燃料的Icg时它们是如何被md2项所主导的。在这个例子中，司机和燃料的局部惯性相应的只有它们各自md2的2.7%和2.1%。

最终我们通过将每个组件贡献的Icg相加得到物体对于自己中性轴的合转动惯量如下：

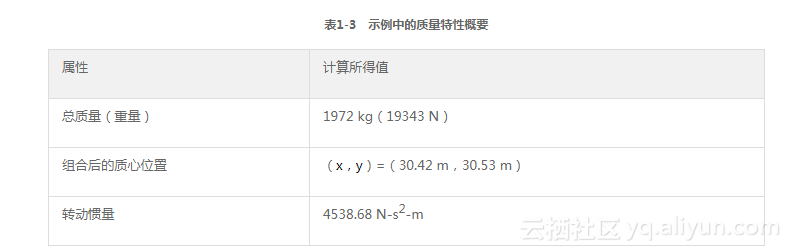
表1-3展示了物体的质量特性，即车、司机和整箱燃料的总和。

清楚地理解这个例子中所展示的概念非常重要，因为当我们接下来过渡到更复杂的系统，尤其是3D中的一般运动时，这些计算只会变得更加复杂。此外，我们需要仿真的物体运动是这些质量特性的函数，其中质量将会决定这些物体会如何被力所影响，质心将会用于追踪位置，而转动惯量将会用于决定在受到不过中心的力时物体如何转动。

至此，我们已经看到了在3D空间中关于三条坐标轴的转动惯量。

但是，在一般3D刚体动力学中，即使局部坐标轴通过物体质心，物体也可能绕任意轴转动，而不是必须绕三条坐标轴之一。这种复杂性表示我们必须给物体的I添加一些项来处理一般转动。我们将会在本章的后面解决这个问题，但是在此之前我们需要详细地复习牛顿第二运动定律。