问题描述:
问题描述:令A【1…n】是一个整形序列,A中的整数a如果在A中出现的次数多于n/2,那么称a为多数元素。试定义数组长度,从键盘随机输入n个数,设计算法寻找多数元素,若从在则输出,否则输出none。
—————————————————————————
思考过程:
我们利用majority算法来进行处理。Majority算法涉及到两个核心步骤。
1.首先我们要了解一个基本归纳结果:如果一组元素中,某一元素为多数元素(我们此时定义的多数元素为元素个数过半的元素)。那么当我们从元素集合中删掉两个不相同的元素,那么之前的多数元素,依然是多数元素。关于这一点利用基本的数学知识可以分析:我们以三个元素为例,假设有
三个元素,其中X1为多数元素,那么存在下面这样的关系:
。当我们删除掉一个X1,一个X2(或X3)后,我们将得到的关系式和1/2做减法,并且进行通分处理,得到下面这个式子:
。因为X1为多数元素,所以X1大于其他元素的数量和,所以分子大于零。而分母部分,显而易见将会大于2*1=2。所以这个式子大于零,那么我们知道,X1类元素此时的个数是X1-1,仍然是多数元素。所以我们的归纳结果显然是正确的。关于更多元素的关系式,我们不再进行推导。
这样,关于这个归纳结果我们已经理解了,再次强调一下:如果一组元素中,某一元素为多数元素(我们此时定义的多数元素为元素个数过半的元素)。那么当我们从元素集合中删掉两个不相同的元素,那么之前的多数元素,依然是多数元素。
下面我们将利用这个结果设计算法。假设有一组元素A[ ],首先我们先取一个元素c=A[1],作为初始假设(假设这个元素为多数元素),那么我们此时去一个标准值count=1。即假设元素在当前元素空间内已经有count=1个。我们将A[2]与c进行比较,如果相等,那么count+1,如果不相等,那么我们将count-1。然后我们进行判断,如果我们的元素空间没有比较结束并且count>0,那么我们继续将A[3]与c进行比较,循环据此进行。如果循环条件不再符合,count=0,那么证明我们刚刚处理的元素空间中,有一个元素占了一半,那么我们正好可以将刚刚处理的元素两两分组,且每组都是不同元素,我们现在放弃刚才处理的元素。在剩下的元素空间中,多数元素并未发生变化,所以我们对剩下的元素空间进行刚刚的处理。这样就形成了递归。最终,我们遍历了整个元素空间,得到一个元素C。第一个核心步骤就已经完成了,我们将其命名为candidate过程。
2.下面我们进行第二个步骤,我们刚刚得到的元素C可能是多数元素,当然也可能是占空间一半的元素,所以进行一个简单比较,计算一下C的个数是否大于1/2,如果为多数元素,那么返回c,如果不是多数元素,那么返回NONE。第二个核心步骤也已完成。
—————————————————————————-
伪代码:
Majority过程:
1.c=candidate(1)
2.count=0
3.for j=1 to n
4. if A[j]=c then count=count+1
5.end for
6.if count>n/2 then return c
7.else return none
Candidate过程:
1.candidate(m)
2.j=m;c=A[m];count=1
3.while j0
j=j+1
4.if A[j]=c then count=count+1
5.else count=count-1
6.end while
7.if j=n then return c
8.else return candidate(j+1)
———————————————————————————————————-
源代码:
程序由python 3.5 环境完成,并由pycharm community 2017 editor IDE 进行编译
import xlrd
from numpy import *
def dataget(exlname,sheetname):
ori = xlrd.open_workbook(exlname)
table = ori.sheet_by_name(sheetname)
data=[]
for i in range(0, table.nrows):
data.append(table.row_values(i))
return data
def condidate(m,A):
j=m
c=A[m]
count=1
while j<len(A)-1 and count>0:
j=j+1
if A[j]==c:
count=count+1
else:
count=count-1
if j==len(A)-1:
return c
else:
return condidate(j+1,A)
def majority(A):
c=condidate(0,A)
count=0
for i in range(0,len(A)-1):
if A[i]==c:
count=count+1
if count>len(A)/2:
return c
else:
return None
if __name__ == '__main__':
data=dataget('majority data.xlsx','Sheet1')
result=majority(data)
print(result)———————————————————————————-
代码讲解:
代码共有四个部分
.
除了candidate()函数和majority()函数外,我们还定义了一个dataget()函数,用来读取数据。我们在一个名称为“majority data.xls”的Excel表格中的Sheet1的A1列中输入我们的数据,保存并放在程序目录中,然后运行程序。
——————————————————————————
今天的文章majority算法及Python 3.5实现分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/61723.html

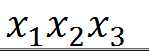 三个元素,其中X1为多数元素,那么存在下面这样的关系:
三个元素,其中X1为多数元素,那么存在下面这样的关系: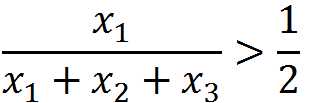 。当我们删除掉一个X1,一个X2(或X3)后,我们将得到的关系式和1/2做减法,并且进行通分处理,得到下面这个式子:
。当我们删除掉一个X1,一个X2(或X3)后,我们将得到的关系式和1/2做减法,并且进行通分处理,得到下面这个式子: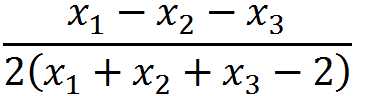 。因为X1为多数元素,所以X1大于其他元素的数量和,所以分子大于零。而分母部分,显而易见将会大于2*1=2。所以这个式子大于零,那么我们知道,X1类元素此时的个数是X1-1,仍然是多数元素。所以我们的归纳结果显然是正确的。关于更多元素的关系式,我们不再进行推导。
。因为X1为多数元素,所以X1大于其他元素的数量和,所以分子大于零。而分母部分,显而易见将会大于2*1=2。所以这个式子大于零,那么我们知道,X1类元素此时的个数是X1-1,仍然是多数元素。所以我们的归纳结果显然是正确的。关于更多元素的关系式,我们不再进行推导。