对抗攻击（Adversarial Attack）

对抗攻击

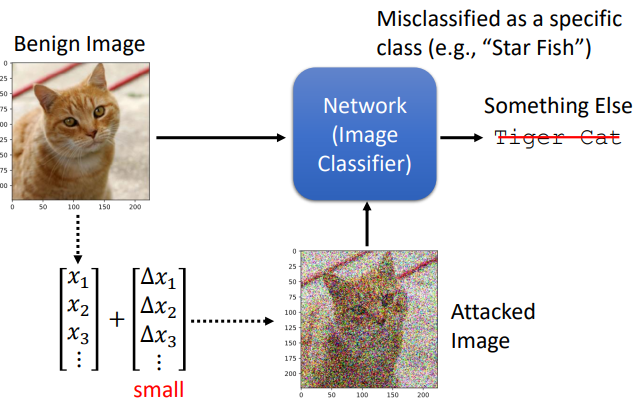
图片可以看成一个很长的向量，如果在图片的每个像素上都加上一个很小的pertubation(扰动、杂讯)，再把它输入到神经网络，这个时候分类器可能就会误判。
没有被攻击的图片一般称为Benign Image，被攻击的图片称为Attacked Image。
通常攻击可以分为定向攻击和非定向攻击：
定向攻击（targeted attack)：误分类成一个特定的类
非定向攻击(non-targeted attack)：误分类成其他类（只要不是cat类）

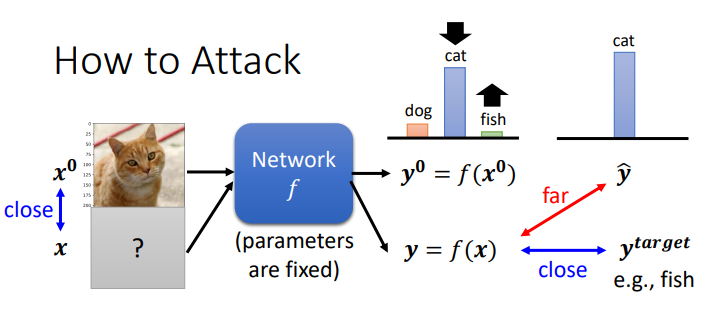
该如何去攻击？
假设benign image是$x^0$，输入到神经网络，输出$y^0=f(x^0)$ ，$x^0$的真实值是 $\hat{y}$
被攻击后输入是$x$，输出$y^0=f(x)$；
想要攻击成功，就得让 $y$ 和 $\hat{y}$ 相差较大

这个问题的loss函数是：
Non-targeted： $L(x)=-e(y,\hat{y})$
targeted： 不仅需要 $y$ 与 $\hat{y}$ 越远越好，还要保证 $y$ 与 $y^{target}$ 越近越好
$$L(x)=-e(y,\hat{y})+e(y,y^{target})$$
另外还期待加入的pertubation越小越好，这样就不容易被人类观察到(not perceived by humans)，即 $x$ 和 $x^0$之间差距越小越好
所以完整的优化问题表达式是：
$$x^{\ast }=arg\underset{d(x^0,x)\le ϵ}{\min }L(x)$$
怎么计算$d(x^0,x)$呢，这里采用的是 L-norm(范数)

• L2-norm：$d(x^0,x)=||\Delta x|{|}^2=(\Delta x_1{)}^2+(\Delta x_2{)}^2+\cdots$
• L-infinity: $d(x^0,x)=||\Delta x|{|}_{\infty }=\max (|\Delta x_1|,|\Delta x_2|,\cdots )$

与神经网络不同更新参数不同的是，对抗攻击是更新输入，同样也用梯度下降的方法，如下图所示：

首先可以从$x^0$开始，然后进行梯度下降，但是迭代过程中要注意限制，保证
$d(x^0,x)\le ϵ$(以L-infinity为例，限制就是需要在以$ϵ$为边长的正方形内)
可以看出，不同的攻击就是有不同的优化方法或者不同的限制。
几种著名的方法：

• FGSM
  论文链接：Explaining And Harnessing Adversarial Examples
  论文笔记链接：click here
  主要思路就是只需要一次迭代就可以达到攻击，另外在对loss求导外面加了一个符号函数sign（大于0输出1，小于0输出-1），这样确保了扰动的限制

• I-FGSM
  FGSM的升级版，即加入迭代版本，让攻击更准确
  论文链接：Adversarial Examples In The Physical World
  论文笔记链接：click here

白盒攻击&黑盒攻击

简单说就是白盒攻击知道模型的参数，黑盒攻击不知道模型的参数

黑盒攻击（black-box attack）

If you have the training data of the target network Train a proxy network yourself
Using the proxy network to generate attacked objects

黑盒攻击，不知道模型的参数，此时该怎么攻击？
如果知道目标网络的训练资料，可以训练一个替代模型，使用替代网络去产生被攻击的对象
那么黑盒攻击容易成功吗？
从论文（Delving into Transferable Adversarial Examples and Black-box Attacks）的实验来看，是容易成功的。
下图的表格，列代表被攻击的模型，行代表代理（proxy）模型。单元格（i，j）表示为模型 i（行）生成的对抗图像在模型 j（列）上评估的准确性。
对角线由于是同一模型，所以看成是白盒攻击。不同行不同列即为黑盒，例如由ResNet-152生成的对抗样本在ResNet-101上的准确率仅为13%。准确率越低，表示攻击越成功。具体可以看这篇 论文笔记

另外还有很多黑盒攻击：

• one-pixel attck
  只需改变一个像素就可以达到攻击的目的
  论文链接：One Pixel Attack for Fooling Deep Neural Networks
  论文笔记链接：click here

• Universal Attack Perturbation（UAP）
  一个通用（与图像无关）和非常小的扰动向量，就可以让攻击成功（以往是针对不同的图像需要设计不同perturbation产生对抗样本）
  论文链接：Universal adversarial perturbations
  论文笔记链接：click here

• BackDoor Attack（后门攻击）
  攻击在训练阶段已经开始，对某张图片加了一些扰动，丢入神经网络进行训练

对抗攻击还被应用在语音，自然语言处理等

对抗防御

1.主动防御
对抗训练

2.被动防御

• 加一个filter（滤波器）
• 图像压缩（先压缩再解压避开攻击）
• Generator（按照对抗样本根据generator生成一张图片）
• Randomization（随机的防御）

参考链接：
https://speech.ee.ntu.edu.tw/~hylee/ml/2022-spring.php

今天的文章对抗攻击（Adversarial Attack）分享到此就结束了，感谢您的阅读。