ECDH算法详解_emd算法

ECDH算法详解

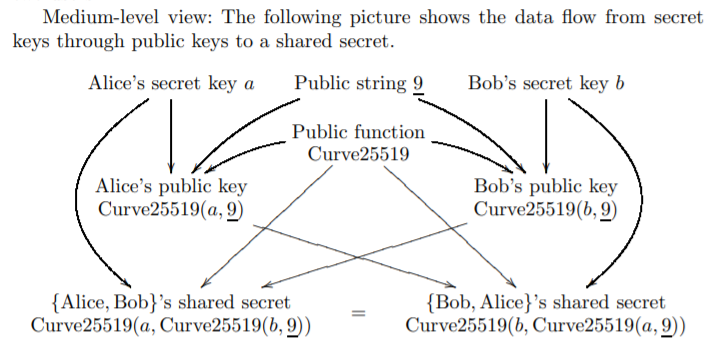
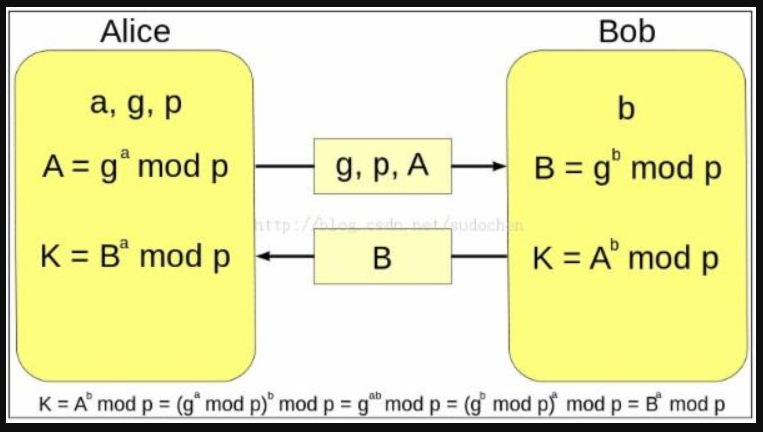
DH密钥交换原理

进一步解释：
两端（Alice 和 Bob）想要安全的交换信息并且第三方不能获取到该信息。当然这也是TLS协议中的目的之一，举个例子。（其实下面的描述其实是ECDHE,而不是ECDH）

• Alice 和 Bob 生成他们自己的私钥和公钥，即 Alice 已知随机数a， 以及一个底数g和一个大质数p；Bob已知随机数b。

• Alice把经过模幂运算的结果A，以及已知的g,p发给Bob，Bob经过运算将B发给Alice。这样Alice 有a,A,B，Bob有b,A,B。

• Alice计算K1（即自己的私钥与Bob的公钥进行模幂运算），同样的，Bob计算K2（自己的私钥与Alice的公钥进行模幂运算）。两边计算的K是相同的。
  

结合ECC椭圆曲线算法

ECDH密钥协商算法是ECC算法和DH密钥交换原理结合使用，用于密钥磋商、。交换双方可以在不共享任何秘密的情况下协商出一个密钥。ECC是建立在基于椭圆曲线的离散对数问题上的密码体制，给定椭圆曲线上的一个点P，一个整数k，求解Q=kP很容易；给定一个点P、Q，知道Q=kP，求整数k则是一个难题。因此ECDH的难点就在于K的求解上。这也是它安全性能进一步提高的表现。
算法举例：

Alice’s 私钥（随机数）:
0xe32868331fa8ef0138de0de85478346aec5e3912b6029ae71691c384237a3eeb
Alice’s 公钥（由Alice的随机数乘上基点）:
(0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba)

Bob’s 私钥（随机数）:
0xcef147652aa90162e1fff9cf07f2605ea05529ca215a04350a98ecc24aa34342
Bob’s公钥（由Bob的随机数乘上基点）:
(0x4034127647bb7fdab7f1526c7d10be8b28174e2bba35b06ffd8a26fc2c20134a, 0x9e773199edc1ea792b150270ea3317689286c9fe239dd5b9c5cfd9e81b4b632)

双方得到的共享密钥:
(0x3e2ffbc3aa8a2836c1689e55cd169ba638b58a3a18803fcf7de153525b28c3cd, 0x43ca148c92af58ebdb525542488a4fe6397809200fe8c61b41a105449507083)

ECDSA签名算法

现在有一个场景：Alice想要用私钥签名一个数据，Bob想要使用Alice的公钥验证这个签名；只有Alice能够进行计算签名然后得到签名，每个人都能验证签名值。

首先Alice和Bob拥有相同的椭圆曲线参数，算法被签名称之为ECDSA，是DSA算法的一个变体。
ECDSA签名算法的输入 是 数据的hash值，而不是数据的本身，hash算法可自选且hash值会被截断。
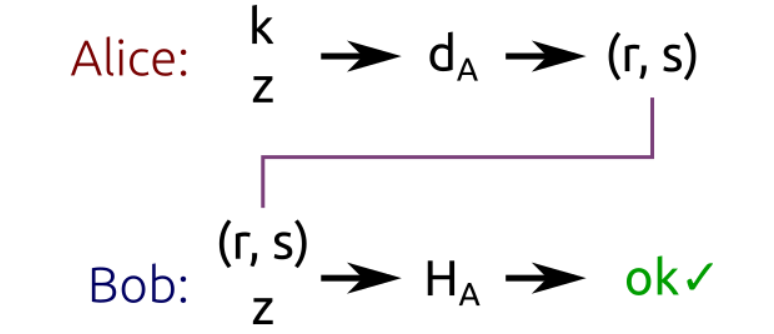
验证流程如下：

上图中，Alice使用私钥da对z进行签名，生成二元组(r, s)。
Bob使用Alice的公钥对(r, s)和Z进行验证。
Bob的验证过程为：
（1）计算u1 = s^-1 * z mod n
（2）计算u2 = s^-1 * r mod n
（3）计算P = u1G + u2Ha
（4）如果r == xp mod n，则验证正确

需要注意的是：当我们使用ECDSA进行签名的时候，k的保密性非常重要。如果我们对所以的签名操作都用一样的k或者我们的随机数生成器存在可预测性，一个攻击者可能会猜出私钥。

参考资料

https://www.jianshu.com/p/b26cd2bfdc28
https://www.orchome.com/1432

今天的文章ECDH算法详解_emd算法分享到此就结束了，感谢您的阅读。