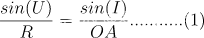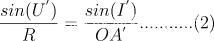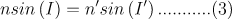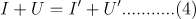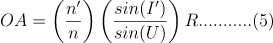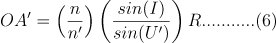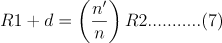齐明点与齐明透镜

薄透镜：
什么叫做齐明透镜：齐明点(aplanatic points)又称为等光程点或不晕点。简单的说就是在此处发出的光线经过折射后可以精确汇聚于一点，没有球差、彗差和像散。

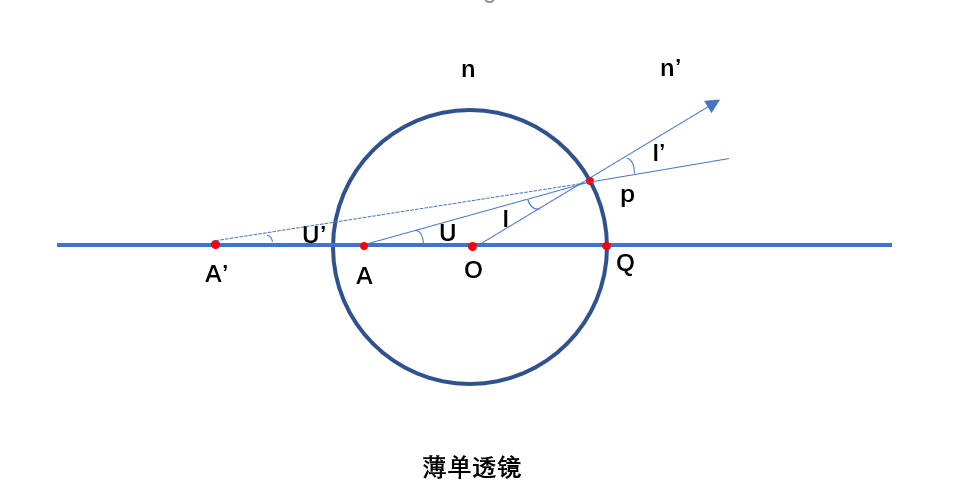
首先，我们分线薄透镜，就是没有厚度的透镜（理想状态），如上图所示，圆心是O点，半径是R，物点在A点，发出入射光线AP，入射角时I， 折射角是I’，像点是A’, 物方孔径角是U，像方孔径角是U’，根据正弦定理，在三角形APO中有：

在三角形A’PO中，有：

又有光线的折射定律：

三角形APO和三角形A’PO中角POQ是三角形的一个角的补角，所以有：

所以由上述三个公式可以得到：

在公式5中，如果我们令OA的长度等于 （n’/n）*R , 那么 sinI’=sinU，也就是I’ = U，再根据公式（4），有 I=U’，所以再公式（6）中，有OA’ = (n/n’) R，这代表着什么呢，也就是说OA等于 (n’/n) R 的情况下，无论我们从入射点以什么角度入射，最终光线的像点（虚像）都在同一个位置，而我们产生像差的原因就是不同角度入射的光线，部分出射光线没有汇聚到同一点所致（球差、像散、慧差等）。所以这样的两个点（A 和 A’）我们称为齐明点。

实际透镜：
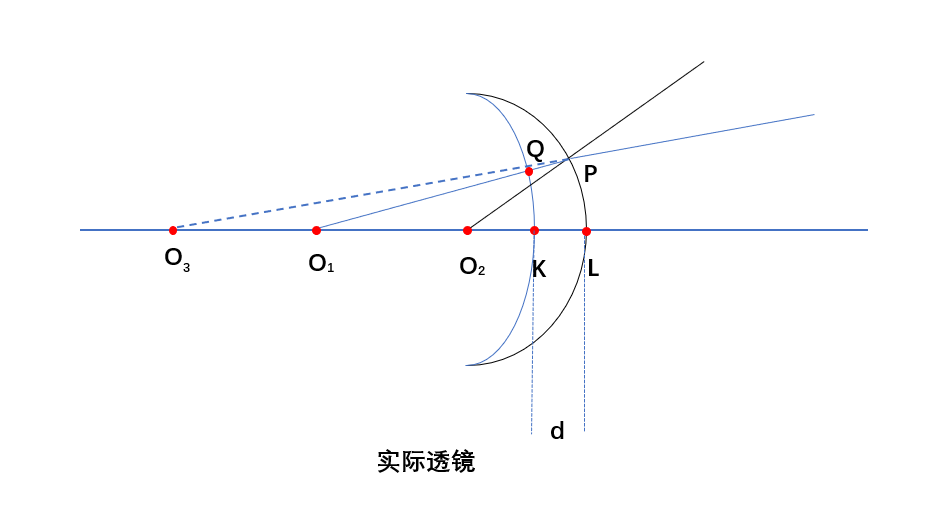
对于实际透镜，它是有厚度的，也就是必定有两个面，所以实际的齐明透镜如下所示：

对于实际的齐明透镜的设计如上图所示，透镜的中心厚度是d，第一个球面的曲率半径为R1，第二个球面的曲率半径为R2，其中O1是从左到右第一个球面的球心，O2是第二个球面的球心，O3是折射光线的反向延长点。例如，光线从O1出发，入射光线是O1Q，由于O1是第一个球面的球心，所以光束不会发生偏折，在经过P点的时候发生偏转，反向延长线交光轴与点O3，根据第一部分薄透镜齐明透镜的推导，如果要使得O3和O1要为一对齐明点，必须满足一下条件：

Zemax仿真验证：
根据第二部分的推到，我们可以先定一组仿真数据，例如：
R1 = 10mm
空气折射率n = 1.0
常用BK7玻璃折射率n’ = 1.5168
d = 3.0mm
根据等式（7）可以得出R2 = 8.5707mm

透镜数据编辑器

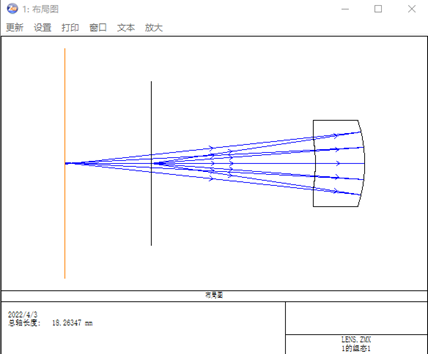
光路仿真图

zemax2013，百度网盘下载地址
提取码：majx

今天的文章齐明点与齐明透镜分享到此就结束了，感谢您的阅读。