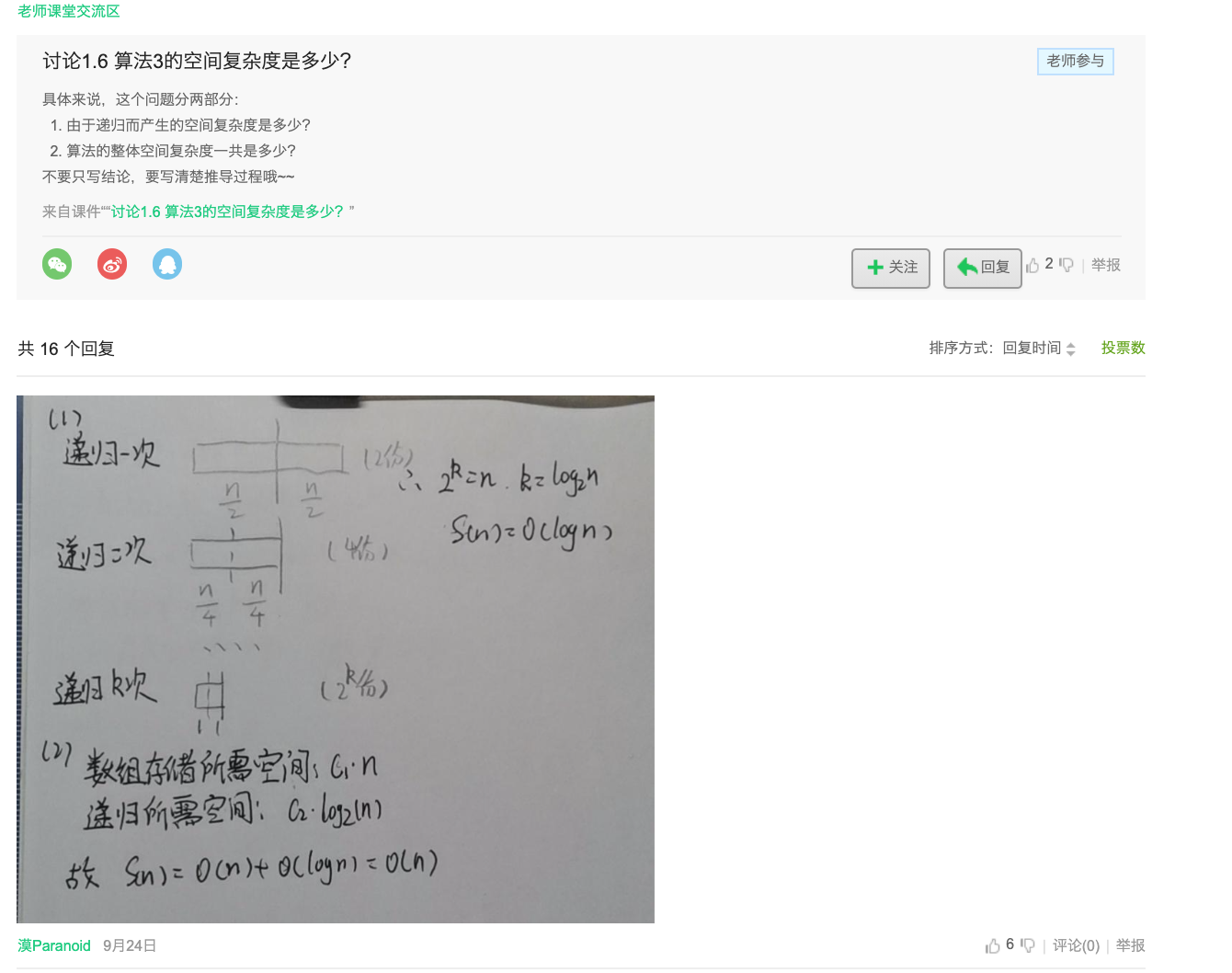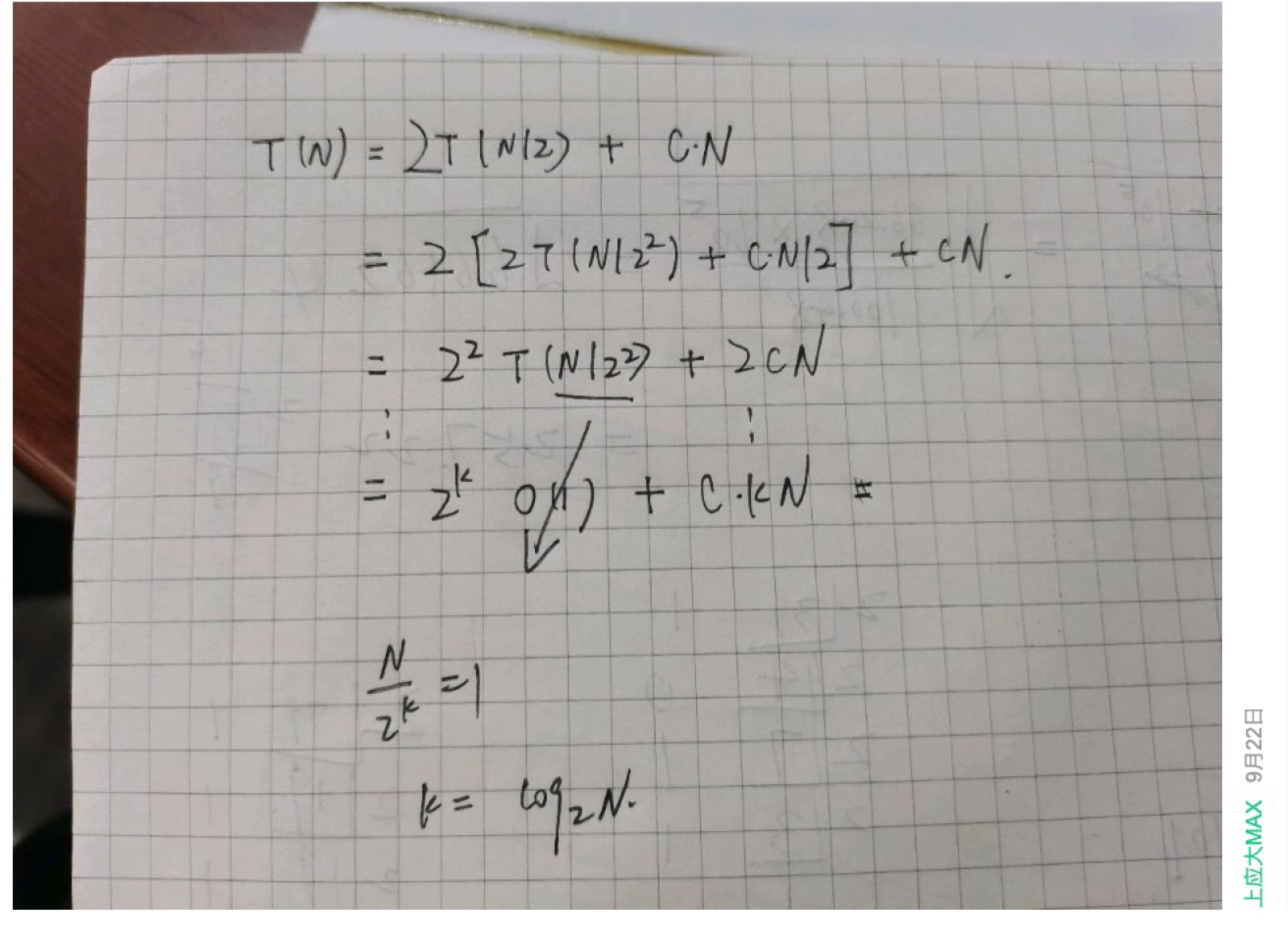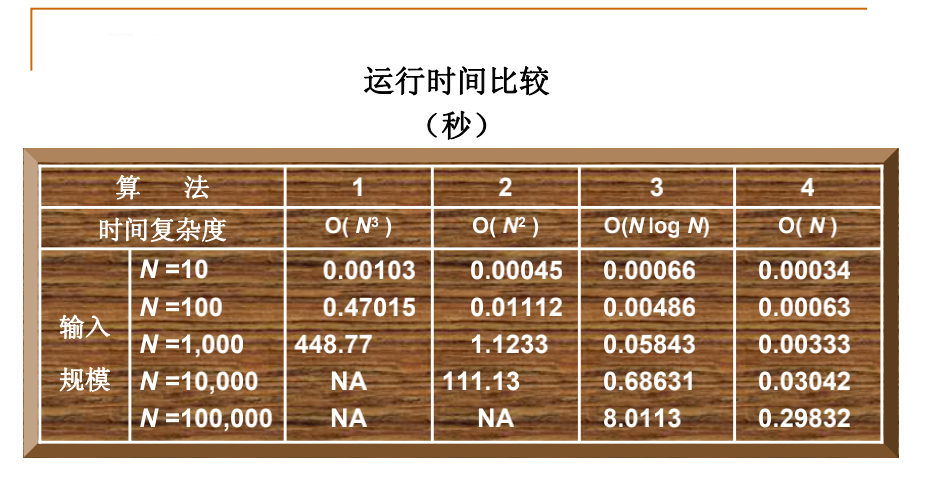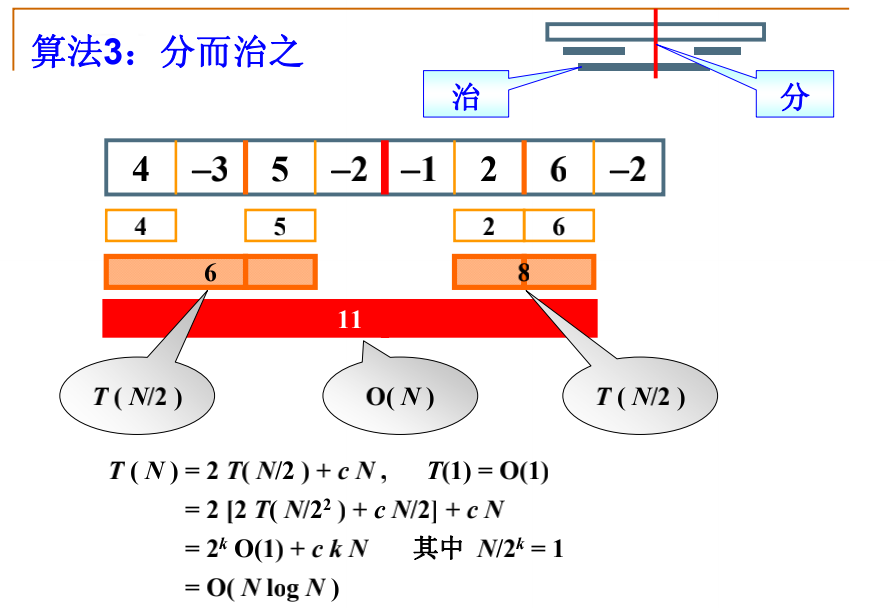
我去,我看完这个分而治之,感觉好神奇啊,但是我不是很懂,所以学习这个地方的时候要好好的品,上网去查资料,那下面讲一下我的理解:
就是在这8个数中间进行分开,左边的再依次分开,右边的依次分开:
就是先把整个分成一半,左边继续分一半,再继续分一半,右边继续分一半,再继续分一半。
分完之后:
的左边的最大子列和就是4,而右边是一个负数,所以返回一个0;
的左边的最大子列和就是5,而右边是一个负数,所以返回一个0;
所以出现了这样一个结果。
的左边是一个负数,所以返回一个0,而右边的最大子列和为2
的左边的最大子列和就是6,而右边是一个负数,所以返回一个0;
所以出现了这样一个结果。
因为求出了这个中间的左边的和右边的最大子列和,但是还有一个跨越边界的最大子列和没有求,求出来跨越边界的最大子列和之后,在这三个中,最大的就是我们要的结果。
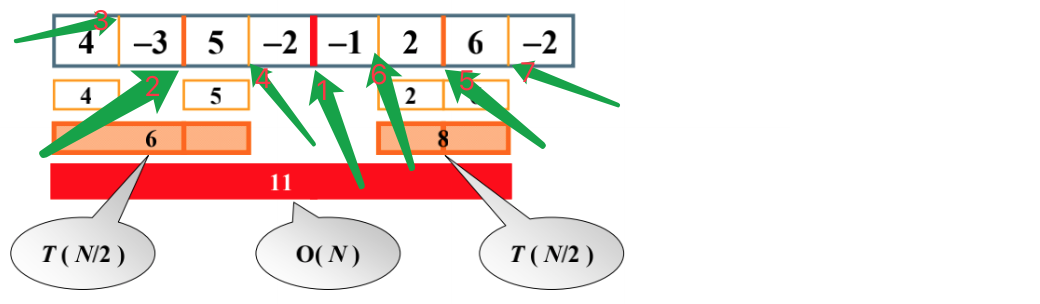
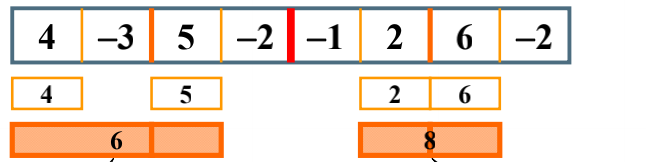
怎么求跨越边界的最大子列和呢,在中间开始往左扫描,-3,1(-3+4),所以左边是1,右边是5,3(5-3),所以跨越边界的最大子列和为1+5=6>5>4,所以这边我们得到的结果是6。同理:
的跨越边界的最大子列和为8>6>2,所以我们得到的这边的结果是8。
同理:
这个的跨边界最大子列和为4+7=11>6>8,故最终结果是11
4=(-2+5-3+4)
7=(-1+2+6)

显然这些代码中只有一个for循环,for循环中的所有的if-else这些东西都是常数数量级的复杂度,所以这个算法的复杂度就是O(n),是线性的。
这个效率比前三个算法都高,那么高的算法效率是有副作用的,副作用就是:它的正确性不是很明显。也就是说,别人要理解这个程序到底是怎样工作的略微有点困难
进行说明:
首先将第一个数-1加入,然后发现这个数小于0,所以当前的子列和是负的,那么直接把它抛弃(因为最大子列和肯定是从正数开始的,负数开始相当于一开始就是负数,所以第一个是负数肯定不能构成最大子列和,故直接把第一个负数抛弃。)
然后第二个数3加入子列和,大于0,将这个值更新为最大子列和。
这个时候子列和加入-2之后,子列和的值为1,大于0,但是ThisSum是比MaxSum要小的,所以不执行if语句,也就是说这个最大子列和MaxSum是不会改变的,同时ThisSum也不会被抛弃,因为现在还是正数,后面总有可能使后面的和变的更大。
这个时候把4加进来,然后最大子列和变成了5,更新最大子列和
这个时候,把-6加进来,整体变成了一个负数,那么就将这些全部舍弃,但是此时的最大子列和没有舍弃
加入1没什么变化,再加入6变成7,比原本的最大子列和要大,所以更新最大子列和
int Max3( int A, int B, int C )
{
/* 返回3个整数中的最大值 */
return A > B ? A > C ? A : C : B > C ? B : C;
}
int DivideAndConquer( int List[], int left, int right )
{
/* 分治法求List[left]到List[right]的最大子列和 */
int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/
int LeftBorderSum, RightBorderSum;
int center, i;
if( left == right ) {
/* 递归的终止条件,子列只有1个数字 */
if( List[left] > 0 ) return List[left];
else return 0;
}
/* 下面是"分"的过程 */
center = ( left + right ) / 2; /* 找到中分点 */
/* 递归求得两边子列的最大和 */
MaxLeftSum = DivideAndConquer( List, left, center );
MaxRightSum = DivideAndConquer( List, center+1, right );
/* 下面求跨分界线的最大子列和 */
MaxLeftBorderSum = 0; LeftBorderSum = 0;
for( i=center; i>=left; i-- ) {
/* 从中线向左扫描 */
LeftBorderSum += List[i];
if( LeftBorderSum > MaxLeftBorderSum )
MaxLeftBorderSum = LeftBorderSum;
} /* 左边扫描结束 */
MaxRightBorderSum = 0; RightBorderSum = 0;
for( i=center+1; i<=right; i++ ) {
/* 从中线向右扫描 */
RightBorderSum += List[i];
if( RightBorderSum > MaxRightBorderSum )
MaxRightBorderSum = RightBorderSum;
} /* 右边扫描结束 */
/* 下面返回"治"的结果 */
return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
int MaxSubseqSum3( int List[], int N )
{
/* 保持与前2种算法相同的函数接口 */
return DivideAndConquer( List, 0, N-1 );
}
今天的文章数据结构1-3-应用实例:最大子列和问题(分而治之、在线处理)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/62379.html




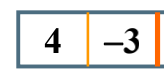 的左边的最大子列和就是4,而右边是一个负数,所以返回一个0;
的左边的最大子列和就是4,而右边是一个负数,所以返回一个0; 的左边的最大子列和就是5,而右边是一个负数,所以返回一个0;
的左边的最大子列和就是5,而右边是一个负数,所以返回一个0;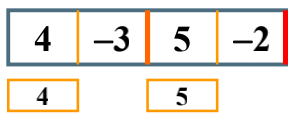 所以出现了这样一个结果。
所以出现了这样一个结果。 的左边是一个负数,所以返回一个0,而右边的最大子列和为2
的左边是一个负数,所以返回一个0,而右边的最大子列和为2 的左边的最大子列和就是6,而右边是一个负数,所以返回一个0;
的左边的最大子列和就是6,而右边是一个负数,所以返回一个0;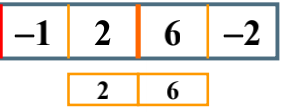 所以出现了这样一个结果。
所以出现了这样一个结果。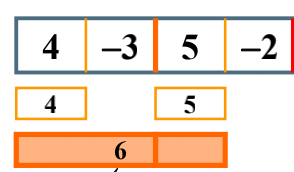
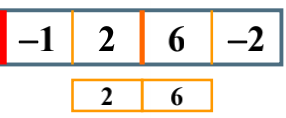 的跨越边界的最大子列和为8>6>2,所以我们得到的这边的结果是8。
的跨越边界的最大子列和为8>6>2,所以我们得到的这边的结果是8。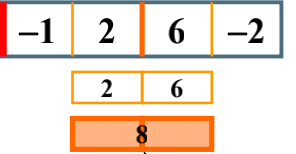
 这个的跨边界最大子列和为4+7=11>6>8,故最终结果是11
这个的跨边界最大子列和为4+7=11>6>8,故最终结果是11