The goal of whitening is to make the input less redundant; more formally, our desiderata are that our learning algorithms sees a training input where (i) the features are less correlated with each other, and (ii) the features all have the same variance.
example
How can we make our input features uncorrelated with each other? We had already done this when computing
. Repeating our previous figure, our plot for
was:
The covariance matrix of this data is given by:
It is no accident that the diagonal values are
and
. Further, the off-diagonal entries are zero; thus,
and
are uncorrelated, satisfying one of our desiderata for whitened data (that the features be less correlated).
To make each of our input features have unit variance, we can simply rescale each feature
by
. Concretely, we define our whitened data
as follows:

Plotting
, we get:
This data now has covariance equal to the identity matrix
. We say that
is our PCA whitened version of the data: The different components of
are uncorrelated and have unit variance.
ZCA Whitening
Finally, it turns out that this way of getting the data to have covariance identity
isn’t unique. Concretely, if
is any orthogonal matrix, so that it satisfies
(less formally, if
is a rotation/reflection matrix), then
will also have identity covariance. In ZCA whitening, we choose
. We define

Plotting
, we get:
It can be shown that out of all possible choices for
, this choice of rotation causes
to be as close as possible to the original input data
.
When using ZCA whitening (unlike PCA whitening), we usually keep all
dimensions of the data, and do not try to reduce its dimension.
Regularizaton
When implementing PCA whitening or ZCA whitening in practice, sometimes some of the eigenvalues
will be numerically close to 0, and thus the scaling step where we divide by
would involve dividing by a value close to zero; this may cause the data to blow up (take on large values) or otherwise be numerically unstable. In practice, we therefore implement this scaling step using a small amount of regularization, and add a small constant
to the eigenvalues before taking their square root and inverse:

When
takes values around
, a value of
might be typical.
For the case of images, adding
here also has the effect of slightly smoothing (or low-pass filtering) the input image. This also has a desirable effect of removing aliasing artifacts caused by the way pixels are laid out in an image, and can improve the features learned (details are beyond the scope of these notes).
ZCA whitening is a form of pre-processing of the data that maps it from
to
. It turns out that this is also a rough model of how the biological eye (the retina) processes images. Specifically, as your eye perceives images, most adjacent “pixels” in your eye will perceive very similar values, since adjacent parts of an image tend to be highly correlated in intensity. It is thus wasteful for your eye to have to transmit every pixel separately (via your optic nerve) to your brain. Instead, your retina performs a decorrelation operation (this is done via retinal neurons that compute a function called “on center, off surround/off center, on surround”) which is similar to that performed by ZCA. This results in a less redundant representation of the input image, which is then transmitted to your brain.
转载于:https://www.cnblogs.com/sprint1989/p/3971244.html
今天的文章Whitening分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/6362.html

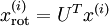 . Repeating our previous figure, our plot for
. Repeating our previous figure, our plot for  was:
was: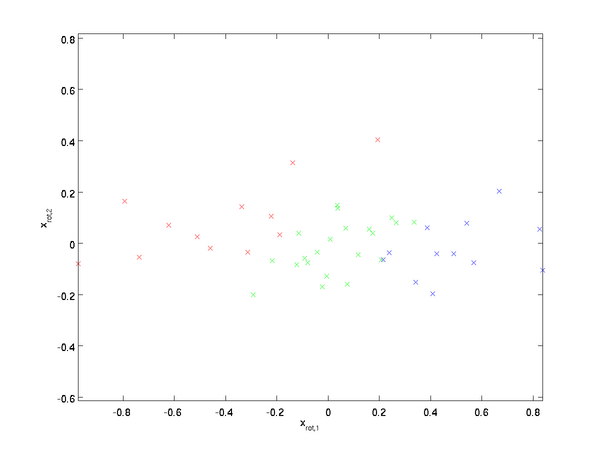
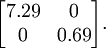
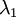 and
and 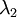 . Further, the off-diagonal entries are zero; thus,
. Further, the off-diagonal entries are zero; thus, 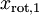 and
and 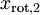 are uncorrelated, satisfying one of our desiderata for whitened data (that the features be less correlated).
are uncorrelated, satisfying one of our desiderata for whitened data (that the features be less correlated).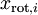 by
by 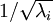 . Concretely, we define our whitened data
. Concretely, we define our whitened data 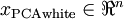 as follows:
as follows: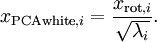
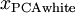 , we get:
, we get: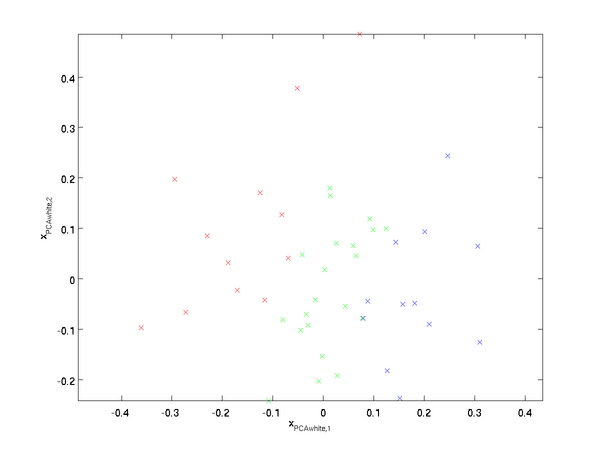
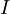 . We say that
. We say that 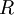 is any orthogonal matrix, so that it satisfies
is any orthogonal matrix, so that it satisfies 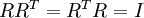 (less formally, if
(less formally, if 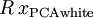 will also have identity covariance. In ZCA whitening, we choose
will also have identity covariance. In ZCA whitening, we choose 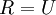 . We define
. We define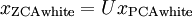
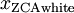 , we get:
, we get: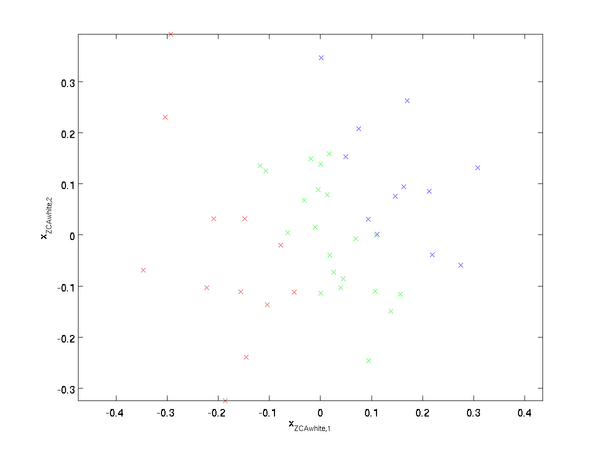
 .
. dimensions of the data, and do not try to reduce its dimension.
dimensions of the data, and do not try to reduce its dimension.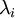 will be numerically close to 0, and thus the scaling step where we divide by
will be numerically close to 0, and thus the scaling step where we divide by 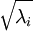 would involve dividing by a value close to zero; this may cause the data to blow up (take on large values) or otherwise be numerically unstable. In practice, we therefore implement this scaling step using a small amount of regularization, and add a small constant
would involve dividing by a value close to zero; this may cause the data to blow up (take on large values) or otherwise be numerically unstable. In practice, we therefore implement this scaling step using a small amount of regularization, and add a small constant 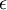 to the eigenvalues before taking their square root and inverse:
to the eigenvalues before taking their square root and inverse: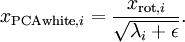
![Whitening插图57 \textstyle [-1,1]](http://deeplearning.stanford.edu/wiki/images/math/8/5/a/85a1c5a07f21a9eebbfb1dca380f8d38.png) , a value of
, a value of 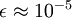 might be typical.
might be typical.