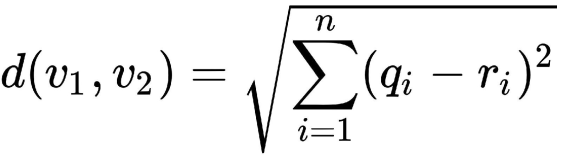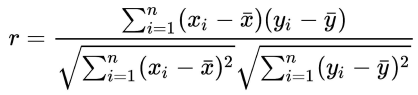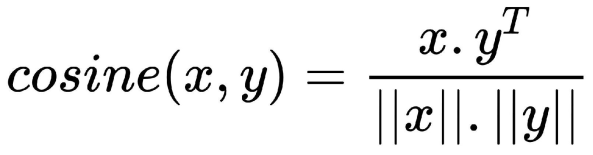Collaborative Filter – Data Mining基础（ACM暑校）

2003年，Amazon公司的Linden、Smith、York大佬刊发了一篇名为《Item-to-Item Collaborative Filtering》的文章；这篇文章首次解释了Amazon公司商品推荐系统的原理。从那时起，这类算法就一直主导着推荐领域。无论是Netflix、Amazon还是Facebook，每一个拥有大量用户群的网站或应用程序都会使用某种形式的协同过滤算法来推荐产品（可能是电影、产品或社交）。协同过滤试图利用社交网络的力量提供可靠、相关、有时甚至令人惊喜的推荐。如果Alice和Bob在很大程度上喜欢同一部电影（比如The Lion King、Aladdin和Toy Story），而爱丽丝也喜欢Finding Nemo，那么没有看过Finding Nemo鲍勃很可能也会喜欢。这样的推荐结果往往符合一类群体的诉求。为了构建稳定的、良好的协同滤波推荐算法，掌握最基本的Data Mining算法是必须的。今天学习主要关注以下部分：

• 相似性测度Similarity measures：对于两个产品，如何从数学上量化它们之间有多不同或相似？相似性度量有助于我们回答这个问题。在ACM暑校培训构建内容推荐引擎时，已经使用了相似性度量（余弦分数）。今天又学到了更多的相似性分数测度方法~~
• 数据降维Dimensionality reduction：在构建协同滤波推荐算法时，通常要处理数百万用户对数百万个产品的评级。在这种情况下，用户和产品向量的维度将达到数百万。为了提高推荐模型的性能、加快计算速度并避免维度爆炸的诅咒，通常最好在保留大部分信息的同时大幅减少维度的数量。
• 监督学习Supervised learning：监督学习是一类机器学习算法，它利用标签数据推断出一个映射函数，然后用它来预测未标记数据的标签（或类）。这里将研究一些最流行的监督学习算法，例如支持向量机、逻辑回归、决策树和嵌套。
• 聚类Clustering：聚类是一种无监督学习，算法试图将所有数据点划分成一定数量的聚类。因此，在不使用标签数据集的情况下，聚类算法能够将类分配给所有未标记的点。在本文中，我们将研究k-means聚类，这是一种简单但功能强大的算法，广泛应用于协同过滤推荐算法中。
• 评估方法Evaluation methods：用于衡量这些算法性能的评估指标。这些指标包括准确性accuracy、精确性precision、召回率recall、F1 score等。

1. 问题背景

协同过滤算法试图解决预测问题。换句话说，我们得到一个i用户和j产品的矩阵。第i行和第j列中的值（用rij表示）表示用户i对第j项给出的评级。我们的工作是完成这个矩阵。换句话说，我们需要预测矩阵中没有数据的所有单元格。例如，在前面的图中，我们被要求预测用户e是否喜欢音乐播放器项。为了完成这项任务，有些评级是可用的（例如用户A喜欢音乐播放器和视频游戏），而其他评级则不可用（例如，我们不知道用户C和D是否喜欢游戏）。

2. 相似性测度

从前面的评分矩阵中，我们看到每个用户都可以表示为一个j维向量，其中第k维表示该用户对第k个产品的评分。假设1表示相似，-1表示不喜欢，0表示没有评级。因此，用户B的偏好向量可以表示为（0，1，-1，-1）。同理，每一个产品也可以表示为一个i维的向量，其中第k个维度表示第k个用对该产品的评级。因此，上图中游戏这个产品可以表示为（1，-1，0，0，-1）。

• 欧氏距离 Euclidean distance

欧几里得距离可以定义为连接在n维笛卡尔平面上绘制的两个数据点的线段长度。欧几里得分数可以取0到无穷大之间的任何值。欧几里得分数（或距离）越低，两个向量之间越相似。

import numpy as np

def euclidean(v1, v2):
    diff = np.power(np.array(v1)- np.array(v2), 2)
    sigma_val = np.sum(diff)
    euclid_score = np.sqrt(sigma_val)
    
    return euclid_score

u1 = [5,1,2,4,5]
u2 = [1,5,4,2,1]
euclidean(u1,u2)

>>> output : 7.483314773547883

• 皮尔逊相关系数 Pearson correlation

考虑两个用户，Alice和Bob，他们同时给相同的五部电影打分。Alice对她的收视率非常吝啬，对任何电影都不超过4分。另一方面，Bob比较开明，在给电影打分时从不给低于2分的分数。计算他们之间的的欧几里得距离如下：

alice = [1,1,3,2,4]
bob = [2,2,4,3,5]
euclidean(alice, bob)

>>> output : 2.2360679774997898

欧几里得距离约为2.23。然而，仔细观察后，我们发现Bob的评分总是比Alice高。因此，我们可以说Alice和Bob的评分是极为相关的。换句话说，如果我们知道Alice对一部电影的评价，我们可以高精度地计算Bob对同一部电影的评价（在本例中，只需添加1）。考虑相反的情况，假设Eve的电影偏好与Alice极端地相反：

eve = [5,5,3,4,2]
euclidean(eve, alice)

>>> output : 6.324555320336759

欧拉分数高达6.32分，表明这两个人非常不同。虽然一个人的评级非常不同，但可以用来准确预测另一个人的相应评级。从数学上讲，认为Alice和Eve的评分有很强的负相关。

欧几里得距离强调幅度，在这个例子中，不能很好地度量两个用户相似或不同的程度。Pearson相关性正可以弥补这个缺陷。Pearson相关性是-1和1之间的一个分数，其中-1表示总负相关（与Alice和Eve的情况一样），1表示总正相关（与Alice和Bob的情况一样），而0表示两个实体之间没有任何关联（或相互独立）。

from scipy.stats import pearsonr
pearsonr(alice, bob)
pearsonr(alice, eve)

>>> output : (1.0, 0.0)  (-1.0, 0.0)

• 余弦相似性 Cosine similarity

余弦相似度分数计算N维空间中两个向量之间角度的余弦。当余弦分数为1（或角度为0）时，向量完全相似。另一方面，余弦分数为-1（或角度180度）表示这两个向量完全不同。不同的相似性评分适用于不同的场景。对于幅度很重要的情况，欧几里得距离是一个合适的度量标准。然而，正如在皮尔逊相关小节中所描述的案例中所看到的，幅度对我们来说不如相关性重要。因此，在构建协同过滤推荐算法时，使用Pearson和余弦相似性分数是最常用的手段。

3. 聚类 Clusterin

协作过滤背后的一个主要想法是，如果用户A对产品的看法与用户B相同，那么A对另一个产品的看法也比随机选择的用户更可能与B相同。聚类是协同过滤算法中最常用的技术之一。它是一种无监督的学习，将数据点分组到不同的类中，使属于特定类的数据点比属于不同类的数据点更相似。这里重点介绍K-means聚类方法。

• k均值聚类 k-means clustering

k均值算法是目前最简单、最流行的机器学习算法之一。它以数据点和簇数k作为输入。接下来，它在平面上随机绘制k个质心。在随机绘制K个质心之后，重复执行以下两个步骤，直到K个质心集不再发生变化。① 将数据点指定给质心：将每个数据点指定给与其最近的质心。分配给特定质心的数据点集合称为簇。因此，对K个质点的分配导致了K簇的形成；② 质心的重新分配：在下一步中，将每个簇的质心重新计算为簇的中心（或簇中所有点的平均值）。然后将所有数据点重新分配给新的质心。

# generating three clusters
from sklearn.datasets.samples_generator import make_blobs
import matplotlib.pyplot as plt
X, y = make_blobs(n_samples=300, centers=3, cluster_std=0.50, random_state=0)
plt.scatter(X[:,0],X[:,1], s=50)
plt.show()

# using k-means cluster
from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=3, init='random', max_iter=10)
kmeans.fit(X)
y_pred = kmeans.predict(X)
plt.scatter(X[:,0], X[:,1], c=y_pred, s=50)
centroids = kmeans.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1], c='black', s=100, marker='X')
plt.show()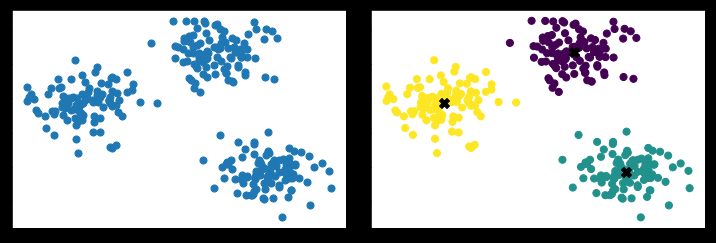

• 其他的聚类算法 Other clustering algorithms

k均值算法虽然功能强大，但并不适用于所有场合（针对cluster呈现高斯分布或近似高斯分布效果最好）。特例如下：

# generating moon-shape samples
from sklearn.datasets import make_moons
x_m, y_m = make_moons(300, noise=0.05, random_state=0)
plt.scatter(x_m[:,0], x_m[:,1], s=50)
plt.show()

# using k-means cluster
kmm = KMeans(n_clusters=2, init='random', max_iter=10)
kmm.fit(x_m)
y_m_pred = kmm.predict(x_m)
plt.scatter(x_m[:,0], x_m[:,1], c=y_m_pred, s=50)
centroids = kmm.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', s=100, marker='X')
plt.show()

# using spectral cluster
from sklearn.cluster import SpectralClustering
model = SpectralClustering(n_clusters=2, affinity='nearest_neighbors')
y_m_sc = model.fit_predict(x_m)
plt.scatter(x_m[:,0], x_m[:,1], c=y_m_sc, s=50)
plt.show()

4. 降维 Dimensionality reduction

随着数据的维度数量增加，大多数机器学习算法往往表现不佳。这种现象通常被称为维数灾难。因此，最好减少数据中特征的数量，同时保留尽可能多的信息。实现这一点有两种方法

① 特征选择 Feature selection：该方法包括识别预测能力最低的特征，并将它们全部删除。因此，特征选择涉及到识别对于特定场景最重要的特征子集。特征选择的一个重要区别是它保持了每个被保留特征的原始含义。例如，假设有一个包含价格、面积和房间数量的住房数据集作为特征。现在，如果我们要取消区域功能，剩余的价格和房间数量功能仍然意味着它们最初的功能。

② 特征提取 Feature extraction：特征提取接收M维数据并将其转换为N维输出空间（通常M>>N），同时保留大部分信息。然而，在这样做的过程中，它创建了没有内在含义的新特性。例如，如果使用相同的住房数据集并使用特征提取将其输出到二维空间中，那么新的特征并不意味着价格、面积或房间数量。

在不讨论深度模型（DeepLearning）之前，常用的数据降维方法就是主成分分析Principle Component Analysis。

• 主成分分析 Principle Component Analysis

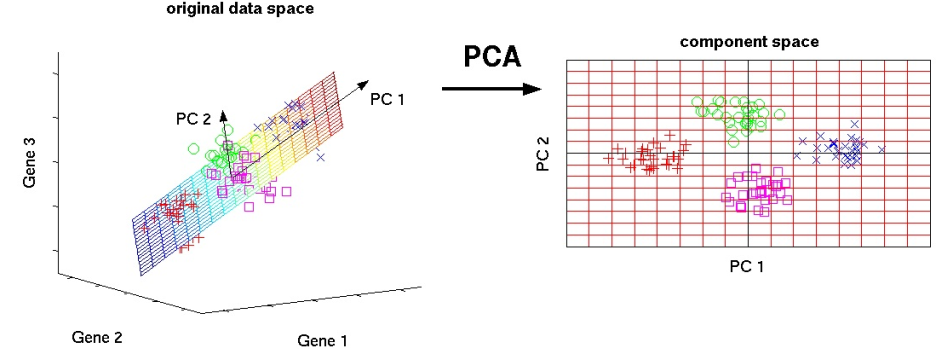
主成分分析是一种无监督特征提取算法，它采用m维输入来创建一组n（m>>n）线性不相关变量（称为主成分），使得n维由于（m-n）维的丢失而损失尽可能小的方差（或信息）。PCA中的线性变换是这样进行的：第一个主分量保持最大方差（或信息）。它是通过考虑那些相互高度相关的变量来实现的。每个主成分比每个后续成分都有更多的方差，并且与前面的成分是正交的。一个基因分析的例子如下：

其他的降维方法如Linear-discriminant analysis、Singular value decomposition因为用的比较少，这里先不做展开讨论。

5. 监督学习

监督学习是一类机器学习算法，它以一系列向量及其相应的输出（连续值或类）作为输入，生成一个可用于映射新实例的推断函数。使用监督学习的一个重要前提是标记数据的可用性。换句话说，我们有必要访问已经知道正确输出的输入。监督学习可以分为两类：分类和回归。分类问题有一组离散的值作为目标变量（例如，喜欢和不喜欢），而回归问题有一个连续的值作为目标（例如，平均评级在1到5之间）。考虑前面定义的评级矩阵。可以将（m-1）列作为输入，将m-th列作为目标变量。这样，应该可以通过传递相应的（m-1）维向量来预测m-th列中的不存在的值。监督学习是机器学习中最成熟的子领域之一，因此，有许多有效的算法可用于执行精确的预测。这里只介绍在各种应用程序（包括协作过滤）中成功使用的一些最流行的算法，当然仍不包含深度学习模型。

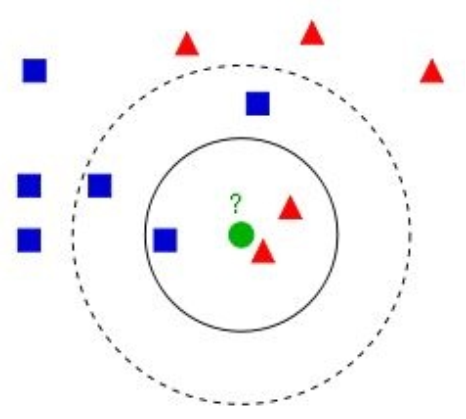
• k最近邻 k-nearest neighbors

k-最近邻（kNN）可能是最简单的机器学习算法。在分类情况下，它通过K最近邻的多数投票结果，将一个类分配给特定的数据点。换言之，数据点被分配给K最近邻中最常见的类。在回归情况下，根据目标变量的k-最近邻计算目标变量的平均值。与大多数机器学习算法不同，KNN本质上是非参数的和懒惰的。前者意味着KNN不会对数据的分布做出任何基础假设。换句话说，模型结构完全由数据决定。后者意味着K-NN几乎不需要任何的训练。它只在预测阶段计算特定点的k-最近邻。

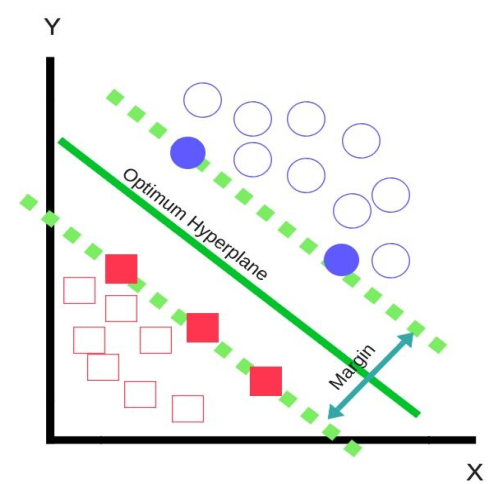
• 支持向量机 Support vector machines

支持向量机是目前工业上应用最广泛的分类算法之一。它以一个n维数据集作为输入，并以类的最大间隔的方式构造（n-1）维超平面。以上图数据的二分类为例；他存在三个可能的超平面（直线），把数据分成两个类。很明显，实线是具有最大的类间隔。换句话说，这个超平面最大限度地分隔了这两个类。超平面下的任何点都将被划分为一个红色的正方形，而上面的任何点都将被划分为一个蓝色的圆。SVM模型只依赖于支持向量；这些点决定了两个类之间可能的最大边界。上图中，实心的正方形和圆形是支持向量，其余数据点对SVM模型并没有任何贡献。其实，通过核函数技巧（如高斯径向核），SVM模型非常适合非线性数据分类，这也是在深度模型出现之前，SVM备受算法研究人员青睐的原因。

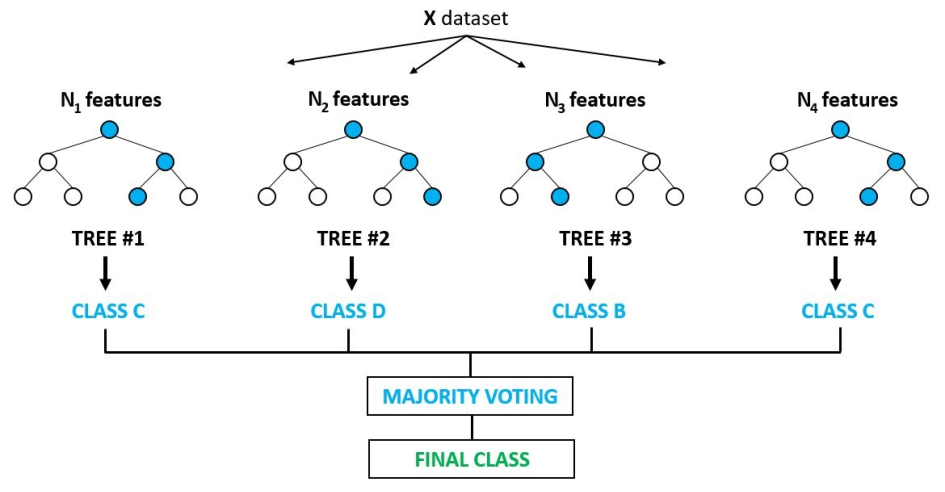
• Ensembling – Bagging and random forests

集成背后的主要思想是多个算法的预测能力远远大于单个算法。决策树是构建集成模型时最常用的基础算法。Bagging是bootstrap aggregating的简称。与大多数其他集成方法一样，对大量基本分类模型进行平均，并对结果平均，以实现最终预测。建立一个bagging模型可以遵循以下步骤：①自助采样；②挑选基类分类器，如决策树，并利用采样后的数据进行训练；③重复训练N个模型，最终的模型输出就是N个分类器的平均输出。Bagging模型的代表是随机森林。除了采样数据点之外，随机森林集成方法还强制每个基础分类器随机选择特征子集（通常是等于特征总数平方根的数字）。选择样本的子集以及特征来构建基础决策树，极大地增强了每一棵树的随机性。这反过来又增加了随机林的鲁棒性，并允许它在有噪声数据的情况下运行得非常好。此外，从特征子集构建基础分类器并分析它们对最终预测的贡献，允许随机森林确定每个特征的重要性。因此，可以使用随机森林进行特征选择。

• Ensembling – Boosting 

由于自助采样的原因，Bagging和随机森林模型所训练的基础分类器是完全彼此依赖的。这个时候Boosting就派上用场了。与随机森林一样，Boosting模型使用样本和特征的子集构建基础分类模型。不同的是，在构建下一个基础分类器的同时，Boosting模型试图纠正前一个分类器所犯的错误。不同的提升算法以不同的方式实现这一点。Boosting一类算法性能非常强大。常常应用在数据科学研究领域。

今天的文章Collaborative Filter – Data Mining基础（ACM暑校）分享到此就结束了，感谢您的阅读。