二维几何变换

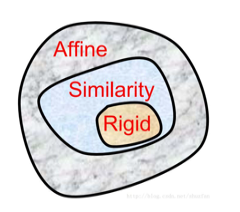
图像的二维几何变换主要包含：刚性变换（rigidity）、相似变换（similarity）、仿射变换（affine）。三者之间的关系如下图所示：

一、齐次坐标

1、什么是齐次坐标

齐次坐标就是用一个n+1维向量表示n维向量

2、为什么要引入齐次坐标？

仿射变换是指在向量空间中进行一次线性变换(乘以一个矩阵)和一次平移(加上一个向量)，变换到另一个向量空间的过程。对于二维坐标系上的一个点（x，y），经过仿射变换后的点的坐标是（u，v），其数学表达式如下：

$\small \begin{bmatrix} u\\ v \end{bmatrix}=A\cdot \begin{bmatrix} x\\ y \end{bmatrix}+B$ ，其中 $\small A=\begin{bmatrix} a &b \\ d& e \end{bmatrix}$ ， $\small B=\begin{bmatrix} c\\ f \end{bmatrix}$

缩放和旋转通过矩阵乘法实现，平移通过矩阵加法实现。通常情况下，几何变换不是单一的，一个物体可能涉及平移、旋转、缩放等多个变换，为了减少计算量，可以将多个变换矩阵合并为一个最终变换矩阵M = [ A B ]。此时几何变换的数学表达式如下：

$\small \begin{bmatrix} u\\ v \end{bmatrix}=M\cdot \begin{bmatrix} x\\ y \end{bmatrix}=\begin{bmatrix} a &b & c\\ d & e & f \end{bmatrix}\cdot \begin{bmatrix} x\\ y \end{bmatrix}$

但我们发现，永远也找不到这样的矩阵M，因为上面的等式是不成立的。为了解决这个问题，我们就增加一个维度，也就是构造齐次坐标矩阵，其数学表达式如下：

$\small \begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=\begin{bmatrix} a & b& c\\ d & e &f \\ 0& 0& 1 \end{bmatrix}=\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$

由上式看出仿射变换矩阵有a、b、c、d、e、f六个未知数，因此至少需要六个方程来求解，即需要三个坐标点对。

二、刚性变换

刚性变换最重要的特点就是变换前后目标 任意两点间距离不变，包含平移、旋转、翻转（镜像）三种。

1、平移

Halcon中向齐次变换矩阵添加平移分量的算子有以下两个：

（1）相对于全局（即固定）坐标系执行平移

hom_mat2d_translate( : : HomMat2D, Tx, Ty : HomMat2DTranslate)

变换矩阵链如下：

$\tiny HomMat2DTranslate=\begin{bmatrix} 1 & 0 & Tx\\ 0 & 1 &Ty \\ 0 &0 & 1 \end{bmatrix}\cdot HomMat2D=\begin{bmatrix} 1 & 0 & Tx\\ 0 & 1 &Ty \\ 0 &0 & 1 \end{bmatrix}\cdot \begin{bmatrix} a & b &c \\ d&e &f \\ 0& 0& 1 \end{bmatrix}=\begin{bmatrix} a & b & Tx+c\\ d & e &Ty+f \\ 0 &0 & 1 \end{bmatrix}$

（2）相对于局部坐标系（即图像原点，左上角）执行平移

hom_mat2d_translate_local( : : HomMat2D, Tx, Ty : HomMat2DTranslate)

变换矩阵链如下：

$\tiny HomMat2DTranslate= HomMat2D\cdot\begin{bmatrix} 1 & 0 & Tx\\ 0 & 1 &Ty \\ 0 &0 & 1 \end{bmatrix}= \begin{bmatrix} a & b &c \\ d&e &f \\ 0& 0& 1 \end{bmatrix}\cdot\begin{bmatrix} 1 & 0 & Tx\\ 0 & 1 &Ty \\ 0 &0 & 1 \end{bmatrix}=\begin{bmatrix} a & b & aTx+bTy+c\\ d & e &dTx+eTy+f \\ 0 &0 & 1 \end{bmatrix}$

注意：齐次矩阵以元组的形式逐行存储，最后一行通常不存储，因为它对于描述仿射变换的所有齐次矩阵都是相同的。如下所示：

$\begin{bmatrix} a & b &c \\ d&e &f \\ 0& 0& 1 \end{bmatrix}$

只存储 [a, b, c, d, e, f]

（3）

举例说明两个平移算子的区别：

dev_close_window ()
dev_open_window (0, 0, 512, 512, 'white', WindowID)
dev_set_draw ('margin')
gen_rectangle1 (Rectangle, 200, 100, 400, 300)
area_center (Rectangle, Area, Row, Column)

*创建一个齐次单位矩阵，并添加缩放分量
hom_mat2d_identity (HomMat2DIdentity)
hom_mat2d_scale (HomMat2DIdentity, 0.5, 0.5,  Row, Column, HomMat2DScale)

*相对于全局坐标系平移
dev_set_color ('green')
hom_mat2d_translate (HomMat2DScale, 5, 5, HomMat2DTranslate1)
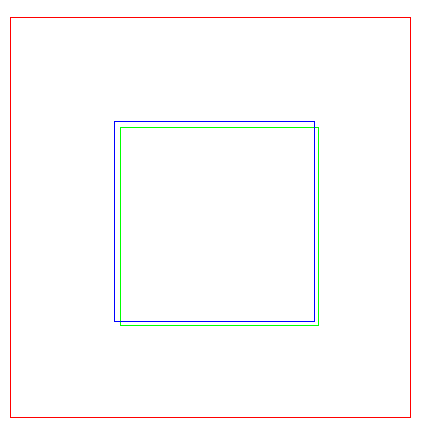
affine_trans_region (Rectangle, RegionAffineTrans1, HomMat2DTranslate1, 'nearest_neighbor')

*相对于局部坐标系平移
dev_set_color ('blue')
hom_mat2d_translate_local (HomMat2DScale, 5, 5, HomMat2DTranslate2)
affine_trans_region (Rectangle, RegionAffineTrans2, HomMat2DTranslate2, 'nearest_neighbor')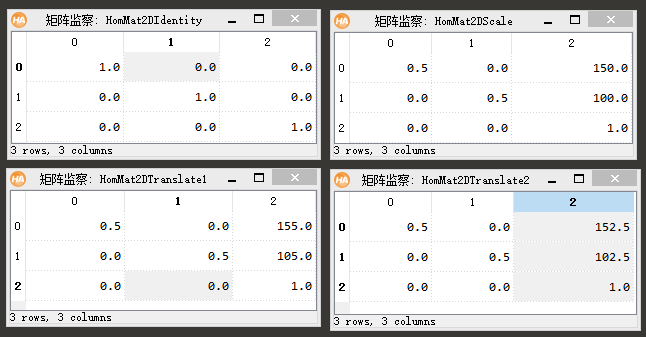

2、旋转（逆时针）

Halcon中向齐次变换矩阵添加旋转分量的算子有以下两个：

（1）相对于全局坐标系执行旋转

hom_mat2d_rotate( : : HomMat2D, Phi, Px, Py : HomMat2DRotate)

点（Px，Py）是变换的不动点，为了实现这种方式，首先在输入变换矩阵中添加一个平移，将不动点移动到全局坐标系的原点上，然后添加旋转，最后把不动点移到原来的位置。变换矩阵链如下：

$\tiny HomMat2DRotate=\begin{bmatrix} 1 & 0 &+ Px\\ 0 & 1 &+Py \\ 0 &0 & 1 \end{bmatrix}\cdot \begin{bmatrix} cos(Phi)& -sin(Phi) & 0\\ sin(Phi) & cos(Phi) &0 \\ 0 &0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -Px\\ 0 & 1 &-Py \\ 0 &0 & 1 \end{bmatrix}\cdot HomMat2D$

$\tiny =\begin{bmatrix} 1 & 0 &+ Px\\ 0 & 1 &+Py \\ 0 &0 & 1 \end{bmatrix}\cdot \begin{bmatrix} cos(Phi)& -sin(Phi) & 0\\ sin(Phi) & cos(Phi) &0 \\ 0 &0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -Px\\ 0 & 1 &-Py \\ 0 &0 & 1 \end{bmatrix}\cdot\begin{bmatrix} a & b &c \\ d&e &f \\ 0& 0& 1 \end{bmatrix}$

$\tiny =\begin{bmatrix} cos(Phi)& -sin(Phi)& -Pxcos(Phi)+Pysin(Phi)+Px\\ sin(Phi)& cos(Phi)&-Pxsin(Phi)-Pycos(Phi)+Py \\ 0& 0 & 1 \end{bmatrix}\cdot\begin{bmatrix} a & b &c \\ d&e &f \\ 0& 0& 1 \end{bmatrix}$

（2）相对于局部坐标系执行旋转(变换的不动点是局部坐标系的原点)

hom_mat2d_rotate_local( : : HomMat2D, Phi : HomMat2DRotate)

变换矩阵链如下：

$\tiny HomMat2DRotate= HomMat2D\cdot\begin{bmatrix} cos(Phi)& -sin(Phi) & 0\\ sin(Phi) & cos(Phi) &0 \\ 0 &0 & 1 \end{bmatrix}$

$\tiny = \begin{bmatrix} a & b &c \\ d&e &f \\ 0& 0& 1 \end{bmatrix}\cdot\begin{bmatrix} cos(Phi)& -sin(Phi) & 0\\ sin(Phi) & cos(Phi) &0 \\ 0 &0 & 1 \end{bmatrix}$

$\tiny =\begin{bmatrix} acos(Phi)+bsin(Phi) & -asin(Phi)+bcos(Phi) & c\\ dcos(Phi)+esin(Phi) & -dsin(Phi)+ecos(Phi) &f \\ 0 &0 & 1 \end{bmatrix}$

（3）那么旋转矩阵是怎么推导出来的呢？如下所示：

在极坐标系下一个点，用长度r与角度 $\tiny \phi$ 表示，在直角坐标系下用(x,y)坐标表示，两者之间的关系如下所示：

$\small x=rcos\phi$

$\small y=rsin\phi$

此时该点旋转角度 $\small \theta$ 得到一个新的点，如下所示：

$\small x^{'}=rcos\left ( \phi+\theta \right )=rcos\phi cos\theta -rsin\phi sin\theta=xcos\theta-ysin\theta$

$\small y^{'}=rsin\left ( \phi+\theta \right )=rcos\phi sin\theta +rsin\phi cos\theta=xsin\theta+ycos\theta$

根据上式得出：

$\small \begin{bmatrix} x'\\ y^{'} \end{bmatrix}=\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta& cos\theta \end{bmatrix}\cdot \begin{bmatrix} x\\ y \end{bmatrix}$

因此旋转矩阵为：

$\small \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta& cos\theta \end{bmatrix}$

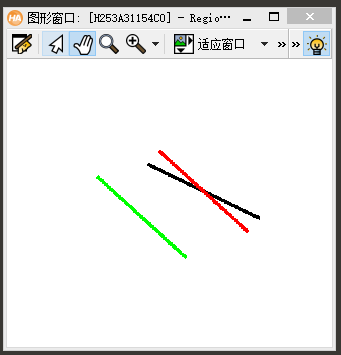
（4）举例说明两个旋转算子的区别：

dev_close_window ()
dev_open_window (0, 0, 512, 512, 'white', WindowID)
dev_set_color ('black')


gen_rectangle2 (Region, 300, 200, -0.5, 100, 2)
area_center (Region, Area, Row, Column)

*创建一个齐次单位矩阵
hom_mat2d_identity (HomMat2DIdentity)

*相对于全局坐标系平移
dev_set_color ('red')
hom_mat2d_rotate (HomMat2DIdentity, -0.3, Row, Column, HomMat2DRotate1)
affine_trans_region (Region, RegionAffineTrans1, HomMat2DRotate1, 'nearest_neighbor')

*相对于局部坐标系平移
dev_set_color('green')
hom_mat2d_rotate_local (HomMat2DIdentity, -0.3, HomMat2DRotate2)
affine_trans_region (Region, RegionAffineTrans2, HomMat2DRotate2, 'nearest_neighbor')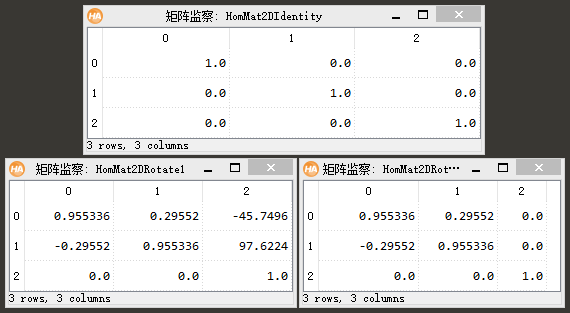

3、反射（镜像）

Halcon中向齐次变换矩阵添加反射分量的算子有以下两个：

（1）相对于全局坐标系执行反射，轴（Px，Py）-（Qx，Qy）在变换中是固定的。

hom_mat2d_reflect( : : HomMat2D, Px, Py, Qx, Qy : HomMat2DReflect)

（2）相对于局部坐标系执行反射，轴（0，0）-（Px，Py）在变换中是固定的。

hom_mat2d_reflect_local( : : HomMat2D, Px, Py : HomMat2DReflect)

（3）Halcon中提供了直接镜像的算子，有 ‘row’，’column’，’diagonal’三种镜像方式

mirror_image(Image : ImageMirror : Mode : )

三、相似变换

相似变换最重要特点就是变换前后目标 形状不变。相比刚性变换，相似变换主要增加了等比缩放。

Halcon中算子如下：

vector_to_similarity( : : Px, Py, Qx, Qy : HomMat2D)

根据两个以上点对近似得到一个相似变换矩阵，包含平移、旋转、等比缩放。

四、仿射变换

仿射变换改变物体位置和形状，但是保持“平直性”（平行线依然保持平行）。相比相似变换，仿射变换主要增加了切变（也叫斜切、错切）、缩放（不要求等比）。

1、斜切

Halcon中向齐次变换矩阵添加斜切分量的算子有以下两个：

（1）相对于全局坐标系执行斜切

hom_mat2d_slant( : : HomMat2D, Theta, Axis, Px, Py : HomMat2DSlant)

一个坐标轴保持不变，另一个坐标轴逆时针旋转角度Theta。参数Axis决定哪个坐标轴倾斜。对于Axis=’x’，x轴倾斜，y轴保持固定；而对于Axis=’y’，y轴倾斜，x轴保持固定。变换矩阵链如下：

$\small Axis='x':HomMat2DSlant=\begin{bmatrix} cos(Theta) & 0 & 0\\ sin (Theta) & 1&0 \\ 0& 0& 1 \end{bmatrix}\cdot HomMat2D$

$\small Axis='y':HomMat2DSlant=\begin{bmatrix} 1 & -sin(Theta) & 0\\ 0 & cos(Theta)&0 \\ 0& 0& 1 \end{bmatrix}\cdot HomMat2D$

点（Px，Py）是变换的不动点，为了实现这种方式，首先在输入变换矩阵中添加一个平移，将不动点移动到全局坐标系的原点上，然后添加旋转，最后把不动点移到原来的位置。当Axis=’x’时，变换矩阵链如下：

$\small HomMatSlant=\begin{bmatrix} 1 & 0&+Px \\ 0 & 1 &+Py \\ 0 & 0& 1 \end{bmatrix}\cdot \begin{bmatrix} cos(Theta) & 0 & 0\\ sin (Theta) & 1&0 \\ 0& 0& 1 \end{bmatrix}\cdot \begin{bmatrix} 1 & 0 & -Px\\ 0 & 1 & -Py\\ 0& 0& 1 \end{bmatrix}\cdot HomMat2D$

（2）相对于局部坐标系执行斜切

hom_mat2d_slant_local( : : HomMat2D, Theta, Axis : HomMat2DSlant)

变换矩阵链如下：

$\small Axis='x':HomMat2DSlant=HomMat2D \cdot \begin{bmatrix} cos(Theta) & 0 & 0\\ sin (Theta) & 1&0 \\ 0& 0& 1 \end{bmatrix}$

$\small Axis='y':HomMat2DSlant=HomMat2D \cdot \begin{bmatrix} 1 & -sin(Theta) & 0\\ 0 & cos(Theta)&0 \\ 0& 0& 1 \end{bmatrix}$

2、缩放

Halcon中向齐次变换矩阵添加反射分量的算子有以下两个：

（1）相对于全局坐标系执行缩放。

hom_mat2d_scale( : : HomMat2D, Sx, Sy, Px, Py : HomMat2DScale)

变换矩阵链如下：

$\small HomMat2DScale=\begin{bmatrix} 1 & 0&+Px \\ 0 & 1 &+Py \\ 0 & 0& 1 \end{bmatrix}\cdot \begin{bmatrix} Sx & 0 & 0\\ 0& Sy&0 \\ 0& 0& 1 \end{bmatrix}\cdot \begin{bmatrix} 1 & 0 & -Px\\ 0 & 1 & -Py\\ 0& 0& 1 \end{bmatrix}\cdot HomMat2D$

（2）相对于局部坐标系执行缩放。

hom_mat2d_reflect_local( : : HomMat2D, Px, Py : HomMat2DReflect)

变换矩阵链如下：

$\small HomMat2DScale=HomMat2D \cdot \begin{bmatrix} Sx & 0 & 0\\ 0& Sy&0 \\ 0& 0& 1 \end{bmatrix}$

五、Halcon中其它几何变换相关算子

1、根据仿射变换矩阵计算仿射变换参数

hom_mat2d_to_affine_par( : : HomMat2D : Sx, Sy, Phi, Theta, Tx, Ty)

2、对像素坐标应用任意仿射二维变换，输入和输出都是亚像素精度，图像坐标系的原点在图像的左上角

affine_trans_pixel( : : HomMat2D, Row, Col : RowTrans, ColTrans)

3、对像素坐标应用任意仿射二维变换，输入和输出都是像素精度，标准图像坐标系，原点在左上角像素的中心

affine_trans_point_2d( : : HomMat2D, Px, Py : Qx, Qy)

4、根据点和角度计算刚性变换矩阵，支持旋转和平移

vector_angle_to_rigid( : : Row1, Column1, Angle1, Row2, Column2, Angle2 : HomMat2D)

5、根据两个以上点对计算刚性变换矩阵，支持旋转和平移

vector_to_rigid( : : Px, Py, Qx, Qy : HomMat2D)

6、根据三个以上点对计算仿射变换矩阵，支持旋转、平移、缩放、斜切

vector_to_hom_mat2d( : : Px, Py, Qx, Qy : HomMat2D)

7、计算齐次二维变换矩阵的行列式

hom_mat2d_determinant( : : HomMat2D : Determinant)

参考文章：二维几何变换

https://zhuanlan.zhihu.com/p/102814853

https://zhuanlan.zhihu.com/p/80852438

http://blog.sina.com.cn/s/blog_c01c55220102yptp.html

今天的文章二维几何变换分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/64022.html

二维几何变换

一、齐次坐标

二、刚性变换

三、相似变换

四、仿射变换

五、Halcon中其它几何变换相关算子

相关推荐

发表回复