1. 无监督学习
机器学习算法可分为监督学习(Supervised learning)和无监督学习(Unsupervised learning)。
监督学习常用于分类和预测。数据集中的所有变量被分为特征和目标,对应模型的输入和输出;数据集被分为训练集和测试集,分别用于训练模型和模型测试与评估。常见的监督学习算法有Regression(回归)、KNN和SVM(分类)。
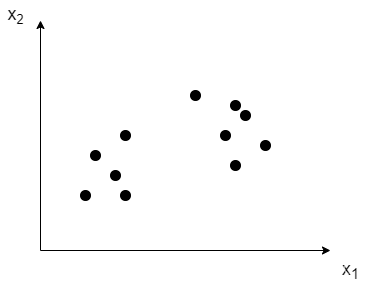
无监督学习常用于聚类。输入数据没有标记,也没有确定的结果,而是通过样本间的相似性对数据集进行聚类,使类内差距最小化,类间差距最大化。常用的无监督学习算法有K-means、 PCA(Principle Component Analysis)。无监督学习中的数据通常是像下面这样。
无监督学习算法的常见应用:
- 市场分割
- 社交网络分析
- 组织计算机集群
- 了解星系的形成
2. 聚类算法
聚类算法又叫做“无监督分类”,试图将数据集中的样本划分成若干个通常是不相交的子集,称之为“簇cluster”。聚类可以作为一个单独过程,用于寻找数据内部的分布结构,也能够作为其他学习任务的前驱过程。聚类算法涉及到的两个问题:性能度量和距离计算。
这种划分可以基于业务需求或建模需求来完成,也可以单纯地帮助我们探索数据的自然结构和分布。比如在商业中,如果手头有大量的当前和潜在客户的信息,可以使用聚类将客户划分为若干组,以便进一步分析和开展营销活动。再比如,聚类可以用于降维和矢量量化,可以将高维特征压缩到一列当中,常常用于图像、声音和视频等非结构化数据,可以大幅度压缩数据量。
聚类算法和分类算法有着很大的不同,如下表所示:
| 聚类 | 分类 | |
|---|---|---|
| 核心 | 将数据分组,探索现实意义 | 从已经分好组别的数据中去学习 |
| 学习类型 | 无监督 | 监督 |
| 典型算法 | K-Means,DBSCAN、层次聚类 | KNN、决策树、Logistics、SVM |
| 算法输出 | 类别数不确定 | 预设好的类别 |
3. K-means
K-Means是聚类算法的典型代表,原理简单。
在K-Means算法中,簇的个数K是一个超参数,需要人为输入来确定。K-Means的核心任务就是根据设定好的K,找出K个最优的质心,并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下:
(1)随机选择K个点,称之为“聚类中心”
(2)对于数据集中的每个数据,按照距离K个中心点的距离,将其和距离最近的中心点关联起来,与同个中心点关联的所有点聚成一类。
(3)计算上面步骤中形成的类的平均值,将该组所关联的中心点移动到平均值的位置
(4)重复上面两个步骤,直到中心点不再变化。
该算法的伪代码如下:
repeat {
# 计算每个样例属于的类
for i= to m
c(i) := index (from 1 to K) of cluster centroid closest to x(i)
# 聚类中心的移动,重新计算该类的质心
for k = 1 to K
u(k) := average (mean) of points assigned to cluster K
}
优缺点分析:
- 简单、速度快、适合发现球形聚类
- K值不好选取,常常缺乏显示可解释性
- 对初始聚类中心敏感,解决方案:多初始化几遍,选取损失函数小的
- 对噪音和异常值的免疫能力较差,不能结局非凸数据
4. 相似度量
通过比较样本之间的相似度,然后将相似度较大的划分为一个类别。那么如何找到这个相似度,或者说找到所谓的“距离最近”的中心点。
4.1 闵科夫斯基距离
闵可夫斯基距离(Minkowski distance)是衡量数值点之间距离的一种非常常见的方法,假设数值点 P 和 Q 坐标如下:
P = ( x 1 , x 2 , … , x n ) and Q = ( y 1 , y 2 , … , y n ) ∈ R n P=\left(x_{1}, x_{2}, \ldots, x_{n}\right) \text { and } Q=\left(y_{1}, y_{2}, \ldots, y_{n}\right) \in \mathbb{R}^{n} P=(x1,x2,…,xn) and Q=(y1,y2,…,yn)∈Rn
那么,闵可夫斯基距离定义为:
d i s t a n c e = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 / p distance = \left(\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|^{p}\right)^{1 / p} distance=(i=1∑n∣xi−yi∣p)1/p
- p = 1时,表示曼哈顿距离;
- p = 2时,表示欧式距离;
- p趋于无穷时,表示切比雪夫距离。
(1)曼哈顿距离
曼哈顿距离又叫出租车距离或者城市区块距离,其形式为:
d i s t a n c e = ∑ i = 1 n ∣ x i − y i ∣ distance = \sum_{i=1}^{n}\left|x_{i}-y_{i}\right| distance=i=1∑n∣xi−yi∣
该距离的意义为标准坐标系下两i但的轴距距离之和,参考下方图片的红线:
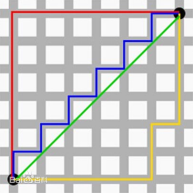
其中红色的线表示的是曼哈顿距离,绿色的线表示的是欧式距离,蓝色的黄色的线表示的是等价的曼哈顿距离。
(2)欧氏距离
欧氏距离就是最常用的空间距离,公式如下:
d ( x , y ) : = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋯ + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 . d(x, y):=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}}=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}} . d(x,y):=(x1−y1)2+(x2−y2)2+⋯+(xn−yn)2=i=1∑n(xi−yi)2.
(3)切比雪夫距离
切比雪夫距离(Chebyshev Distance)为L∞度量,是向量空间中的一种度量,二个点之间的距离定义是其各坐标数值差绝对值的最大值。以数学的观点来看,切比雪夫距离是由一致范数(或称为上确界范数)所衍生的度量,也是超凸度量的一种:
d ( x , y ) = max ( ∣ x i − y i ∣ ) \mathrm{d}(\mathrm{x}, \mathrm{y})=\max \left(\left|\mathrm{x}_{\mathrm{i}}-\mathrm{y}_{\mathrm{i}}\right|\right) d(x,y)=max(∣xi−yi∣)
4.2 余弦距离
利用闵可夫斯基度量对高维数据进行聚类通常是无效的,因为样本之间的距离随着维数的增加而增加。余弦距离测量两个矢量之间的夹角,而不是两个矢量之间的幅值差。它适用于高维数据聚类时相似度测量。
cos ( x ⃗ , y ⃗ ) = y ⃗ T x ⃗ ∥ x ⃗ ∥ ∥ y ⃗ ∥ \cos (\vec{x}, \vec{y})=\frac{\vec{y}^{T} \vec{x}}{\|\vec{x}\|\|\vec{y}\|} cos(x,y)=∥x∥∥y∥yTx
最常见的应用就是计算文本相似度。将两个文本根据他们词,建立两个向量,计算这两个向量的余弦值,就可以知道两个文本在统计学方法中他们的相似度情况。
4.3 马氏距离
马氏距离(Mahalanobis Distance)是一种距离的度量,可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题。
单个数据点的马氏距离:
D M ( x ) = ( x − μ ) T Σ − 1 ( x − μ ) D_{M}(x)=\sqrt{(x-\mu)^{T} \Sigma^{-1}(x-\mu)} DM(x)=(x−μ)TΣ−1(x−μ)
数据点x, y之间的马氏距离:
D M ( x , y ) = ( x − y ) T Σ − 1 ( x − y ) D_{M}(x, y)=\sqrt{(x-y)^{T} \Sigma^{-1}(x-y)} DM(x,y)=(x−y)TΣ−1(x−y)
其中Σ是多维随机变量的协方差矩阵,μ为样本均值,如果协方差矩阵是单位向量,也就是各维度独立同分布,马氏距离就变成了欧氏距离。
通过协方差矩阵,马氏距离考虑到了各个属性之间的联系。马氏距离在非奇异变换下是不变的,可用来检测异常值(outliers)。
5. 优化目标
K-均值最小化问题,是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和。对于一个簇来说,所有样本点到质心的距离之和越小,便认为这个簇中的样本越相似,簇内差异越小。当使用欧氏距离时,代价函数(畸变函数Distortion function):
J ( c ( 1 ) , … , c ( m ) , μ 1 , … , μ K ) = 1 m ∑ i = 1 m ∣ X ( i ) − μ c ( i ) ∣ 2 J\left(c^{(1)}, \ldots, c^{(m)}, \mu_{1}, \ldots, \mu_{K}\right)=\frac{1}{m} \sum_{i=1}^{m}\left|X^{(i)}-\mu_{c^{(i)}}\right|^{2} J(c(1),…,c(m),μ1,…,μK)=m1i=1∑m∣
∣X(i)−μc(i)∣
∣2
其中μ代表与xi最近的聚类中心点,优化目标就是找出使得代价函数最小的c和μ。
实际上,在聚类算法中簇的中心不断变化不断迭代的过程中,总体平方和是越来越小的。而且显而易见,当整体平方和达到最小值的时候,质心就不再发生变化了。如此,K-Means的求解过程,就变成了一个最优化问题。
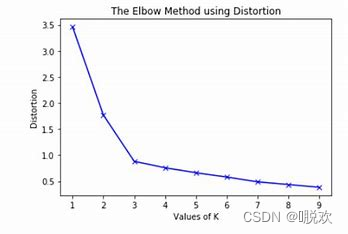
在K-Means中,在一个固定的簇数K条件下,最小化总体平方和来求解最佳质心,并基于质心的存在去进行聚类。而在不知道簇数K的条件下,显然K越多畸变程度就越小,当K等于样本数量时畸变程度就为零,那么肯定通过畸变程度选择K。这里通常会选择肘部法则。
肘部法则是指:畸变程度会随着类别的增加而降低,但对于有一定区分度的数据,在达到某个临界点时畸变程度会得到极大改善,之后缓慢下降,这个临界点就可以考虑为聚类性能较好的点。
如该图所示,根据肘部法则,聚类数为3时是一个不错的选择。
然而,实际运用中,对于K值的选取,如果完全依赖于肘部法则,那么很有可能算法的结果难以得到一个合理科学的解释。因此,往往需要结合实际情况综合评判分析,选择一个想要的K。
6. 模型评估
在算法迭代中,我们以畸变程度最小化为目标进行优化,因此畸变程度肯定是一个可以给作为模型评估的指标。这里介绍一下其它的评估指标。
6.1 轮廓系数
在大部分的情况下,是对没有真实标签的数据进行探索,也就是对不知道真正答案的数据进行聚类。这样的聚类,是完全依赖于评价簇内的稠密程度(簇内差异小)和簇间的离散程度(簇外差异大)来评估聚类的效果。其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的,它能够同时衡量:
- 样本与其自身所在的簇中的其他样本的相似度a,等于样本与同一簇中所有其他点之间的平均距离。
- 样本与其他簇中的样本的相似度b,等于样本与下一个最近的簇中的所有点之间的平均距离。
根据聚类“簇内差异小,簇外差异大”的原则,我们希望b永远大于a,并且大得越多越好。单个样本的轮廓系数计算为:
s ( i ) = b ( i ) − a ( i ) max { a ( i ) , b ( i ) } s(i)=\frac{b(i)-a(i)}{\max \{a(i), b(i)\}} s(i)=max{
a(i),b(i)}b(i)−a(i)
a(i) 表示样本i与其所在簇内其他样本的平均距离,b(i) 表示样本i与其他簇样本的平均距离。聚类总的轮廓系数SC为:
S C = 1 N ∑ i = 1 N s ( i ) S C=\frac{1}{N} \sum_{i=1}^{N} s(i) SC=N1i=1∑Ns(i)
轮廓系数取值范围为[-1,1],取值越接近1则说明聚类性能越好,相反,取值越接近-1则说明聚类性能越差。轮廓系数最高的簇的数量表示簇的数量的最佳选择。
6.2 兰德系数
兰德系数(Rand index)需要给定实际类别信息C,假设K是聚类结果。
- a:在C与K中都是同类别的元素对数
- b:在C与K中都是不同类别的元素对数
则兰德系数为:
R I = a + b C 2 n samples R I=\frac{a+b}{C_{2}^{n_{\text {samples }}}} RI=C2nsamples a+b
分母:任意两个样本为一类有多少种组合,是数据集中可以组成的总元素对数;分子:属性一致的样本数,即同属于这一类或都不属于这一类。a是真实在同一类、预测也在同一类的样本数;b是真实在不同类、预测也在不同类的样本数。
RI取值范围为[0,1],值越大意味着聚类结果与真实情况越吻合。
对于随机结果,RI并不能保证分数接近零。为了实现“在聚类结果随机产生的情况下,指标应该接近零”,调整兰德系数(Adjusted rand index)被提出,它具有更高的区分度:
A R I = R I − E [ R I ] max ( R I ) − E [ R I ] A R I=\frac{R I-E[R I]}{\max (R I)-E[R I]} ARI=max(RI)−E[RI]RI−E[RI]
ARI取值范围为[-1,1],值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲,ARI衡量的是两个数据分布的吻合程度。
优缺点分析:
- 对任意数量的聚类中心和样本数,随机聚类的ARI都非常接近于0
- ARI需要真实标签
- 可用于聚类算法之间的比较
今天的文章聚类分析相似度的测度_聚类分析结果优劣标准分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/64339.html