梁的弹性模量怎么算_根据应力应变曲线求弹性模量「建议收藏」

 现在大多数道桥设计院都拥有几种结构计算软件，对重要结构，都要用不同的软件相互复核。这是技术进步的大好事。本文介绍的梁格法，虽然是人人皆知，但是误区也不少，所以觉得有必要再把它清晰、准确地介绍一下，希望对设计人员有益、对工程有益。

梁格法是唯一既有相当精度又比较容易实行的方法

对曲线梁桥，可以把它简化为单根曲梁、平面梁格计算，也可以几乎不加简化地用块体单元、壳单元计算。

单根曲梁模型的优点是简单，缺点是：几乎所有类型的梁单元都有刚性截面假定、因而不能考虑桥梁横截面的畸变，总体精度较低。

块体单元、壳单元模型，优点：与实际模型最接近，不需要计算横截面的形心、剪力中心、翼板有效宽度，截面的畸变、翘曲自动考虑；缺点：输出的是梁横截面上若干点的应力，不能直接用于强度计算。对于位置固定的静力荷载，当然可以把若干点的应力换算成横截面上的内力。对于位置不固定的车辆荷载，理论上必须采用影响面方法求最大、最小内力。板壳单元输出的只能是各点的应力影响面。把各点的应力影响面重新合成为横截面的内力影响面，要另外附加大量工作。这个缺点使得它几乎无可能在设计中应用。

梁格法优点：可以直接输出各主梁的内力，便于利用规范进行强度验算，整体精度能满足设计要求。由于这个优点，使得该法成为计算曲线梁桥和其它平面形状特殊的梁式桥的唯一实用方法。缺点：它对原结构进行了面目全非的简化，大量几何参数要预先计算准备，如果由计算者手工准备，不仅工作量大，而且人为偏差较难避免。

如何建立梁格力学模型

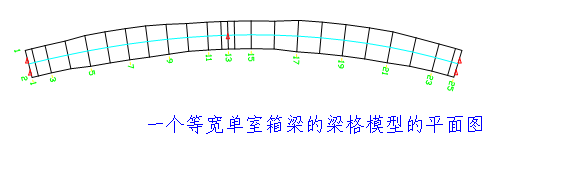
纵梁个数、横梁道数、支点、梁单元

对于有腹板的箱型、T型梁桥，其梁格模型中纵向主梁的个数，应当是腹板的个数。对于实心板梁，纵向主梁的个数可按计算者意愿决定。全桥顺桥向划分M个梁段，共有M+1个横截面，每个横截面位置，就是横向梁单元的位置。支点应当位于某个横截面下面，也就是在某个横梁下面。每一道横梁都被纵向主梁和支点分割成数目不等的单元。纵、横梁单元用同一种最普通的12自由度空间梁单元，能考虑剪切变形影响即可。有的软件，比如ANSYS,还另外提供了近10种类型的梁单元，比如横截面是工型的梁单元，在这里都用不上，原因后述。

纵向主梁的划分、几何常数计算

对于箱型梁桥，从什么地方划开，使其成为若干个纵向主梁？汉勃利[1]提出了一个原则：应当使划分以后的各工型的形心大致在同一高度上。笔者曾经用有限条法进行过考核，发现，按照他这个原则，从各主梁弯矩、剪力计算出的正应力、剪应力，与有限条的吻合性确实比较好。

具体划分步骤，应当是试算的：

(1)在箱型各室的顶板、底板各选择一划分点，成为若干个工型

(2)对各工型的翼板计算有效宽度

(3)按有效宽度计算各工型形心的竖向位置

(4)比较各工型的形心高度，若不在一条直线上且偏离较大，返回(1)重新来

看来，完全满足汉勃利的原则，是相当难的。

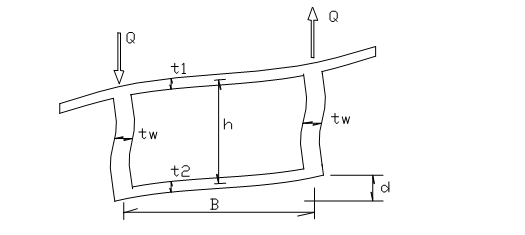
需要计算的纵向主梁几何常数：工型的全面积、抗剪面积，考虑有效宽度的形心位置、两个弯曲惯矩，绕水平纵轴的自由扭转惯矩。自由扭转惯矩计算错误较多。汉勃利[1]的自由扭转惯矩计算公式是

C=2*h*h*t1*t2/(t1+t2)

其中，C—单位宽度顶、底板联合自由扭转惯矩，h—顶、底板中面间距，t1、t2—顶、底板平均厚度。C值乘以顶、底板平均宽度，得工型一侧的扭转惯矩。工型另一侧的扭转惯矩同法计算再相加。

如果只有顶板或是实心板，则

C=t*t*t/6

注意：按上面方法算得的各主梁扭转惯矩之和，只等于整体横截面自由扭转惯矩的1/2。是不是少算了1/2？没有少。另外1/2的扭转惯矩是各主梁竖向抗剪效应提供的。

还要指出：工型的形心的横向位置，就取在腹板的厚度中线上，不需要计算，其竖向位置，则应按计算值。

由于不是按照工型翼板实际宽度计算截面几何常数，ANSYS、SUP2000等提供的特殊截面梁单元，都不能应用。

横梁几何常数计算

横梁代表的是指定横截面两侧各1/2纵向梁单元长度范围内的顶、底板和横隔板。对顶、底板，需要计算单位宽度的抗弯惯矩、等效抗剪面积、抗扭惯矩，再乘以横梁代表的宽度，再迭加横隔板(如果该位置有的话)的相应常数。

抗扭惯矩与前面的公式相同。要不要计算、怎样计算箱型梁的横向抗剪刚度，在许多人常发生错误。

汉勃利[1]的单位宽度等效抗剪面积公式是

(1)      对于箱型梁的顶、底板

As=E/G* (t1*t1 + t2*t2)*tw**3 / (B**3*tw + (t1*t1+t2*t2)*B*h)

其中E、G—混凝土的弹性模量、剪切模量，其它变量见下图。

汉勃利根据闭合框架推导出箱形截面的横向等效抗剪面积

如果只有顶板或是实心板

As=t1*5/6

梁格模型节点的平面坐标

各截面处各工型的形心的平面坐标，或者说是水平形心主轴与各腹板中线交点的平面坐标，就是梁格纵向主梁节点的平面坐标。这样一来，实际上等宽度的桥梁，由于它的腹板在中墩附近向箱内加厚，对应的梁格模型，就不会是等宽度的了，在中墩附近变窄，见下图。

梁格力学模型的深一步讨论

梁格力学模型是平面的吗？

在梁格模型里，纵向主梁单元是沿着它的形心走的。变高度梁的形心也是变高度的。即使是等高度梁，由于底板加厚、考虑翼板有效宽度，形心高度也有变化。这两种情况下的的形心位置，都是跨间高、墩台附近低，象拱一样。所以梁格模型不应当是平面的。对于刚构体系的梁桥，如果能建立变高度的梁格模型，“拱”的效应就可以计算出来。对与连续梁，采用平面梁格应当足够了。

梁格力学模型是直接摆放在支点上吗？

既然在梁格模型的纵向主梁单元是沿着它的形心走的，那么在支点截面，形心是在支点上方一定高度，梁格模型不应当直接摆放在支点，而应当通过竖向刚臂与支点联系，象个有腿的长条板凳一样。板凳腿的高度还值得讨论。按照经典的弹性薄壁杆理论，弯曲变形是绕着形心发生的，扭转变形是绕着剪力中心发生的。所以，在计算弯曲效应时，板凳腿取形心高度，在计算扭转效应时，板凳腿取剪力中心高度。但弯曲和扭转是同时发生的，板凳腿有两种高度，会不会把变形“卡死”？不会，因为在这里我们只是做了个数字游戏，并没有在同一位置上安装一长一短两个刚臂。

计算车辆荷载效应及内力组合

这项计算取决于所用的软件能否计算梁格模型的内力影响面，和对影响面动态布载。如果没有这功能，麻烦就大了，只能对确定的荷载进行复核性计算了。顺便说明，与影响面方法对应的，还有一种叫做内力横向分配理论的方法，见参考文献2。从理论上说，两种方法的结果，都覆盖了曲线梁桥所有部位的最大最小内力，数值虽然有差别，都是安全的。影响面方法更精确一些，但缺点是它不能计算全桥扭矩包络图，而内力横向分配方法可以。扭矩包络图对曲线梁桥设计计算非常重要。笔者接触了多起曲线梁桥支座脱空、侧翻、爬移事故，它们在设计时用的软件，不可谓不高级，但共同特点是都不能输出扭矩包络图，它们的中墩偏心设置，全是盲目的。由于这个原因，笔者的软件里仍然保留着内力横向分配方法。

计算预应力

对曲线梁桥进行预应力计算，必须计算横截面的剪力中心。笔者仔细研究了目前广泛应用的4个结构/桥梁分析软件，发现：只有ANSYS的Beam24属弹性薄壁杆单元，可以计算单室薄壁杆截面的剪力中心。单箱双室截面，只要左右对称，可以把中腹板略去后按单室截面计算。除此之外的截面，ANSYS也没办法了。

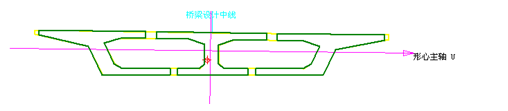
程序计算的非对称截面的主梁划分、有效宽度、形心主轴、剪力中心图

预应力钢索要用等效的空间力代替。钢索等效空间力是：竖向分力、水平分力、轴向压力、轴向压力绕主形心轴U(大致水平)的力矩、水平分力绕剪力中心轴的力矩，共5项。因为钢索分别归属于各主梁，它们的空间力也相应地作用于各主梁，所以轴向压力绕主形心轴V(大致垂直)的力矩、竖向分力绕剪力中心轴的力矩就不需要考虑了。

钢索化为等效空间力之前，要扣除各项应力损失。摩擦损失、回缩损失、松弛损失尚可手算，徐变应力损失只能在梁格的徐变计算中同步得到，或者利用近似公式计算。