如何评估随机森林模型以及重要预测变量的显著性

如何评估随机森林模型以及重要预测变量的显著性

说到随机森林（random forest，RF），想必很多同学都不陌生了，毕竟这些机器学习方法目前非常流（fàn）行（làn）……白鱼同学也曾分别分享过“随机森林分类”以及“随机森林回归”在R语言中实现的例子，包括模型拟合、通过预测变量的值预测响应变量的值、以及评估哪些预测变量是“更重要的”等。在这两篇推文中，都是使用randomForest包执行的分析。不过在实际应用中，比方说想模仿一些文献的分析过程时，却发现某些统计无法通过randomForest包实现？

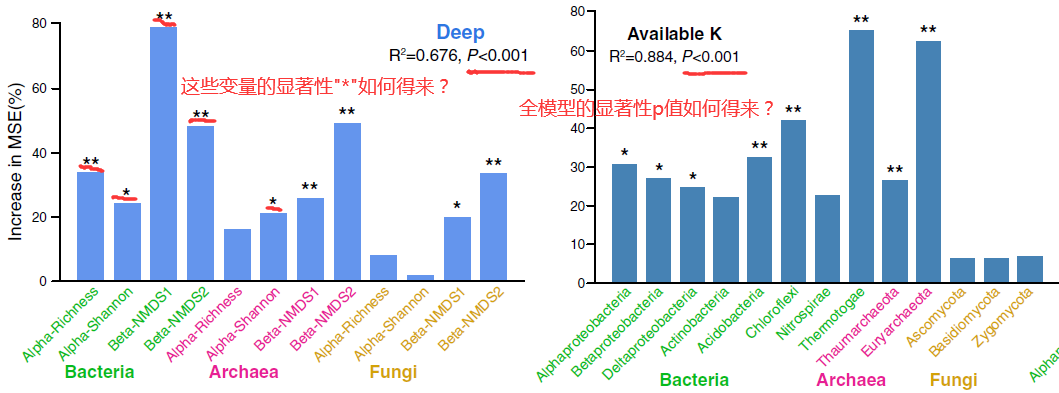
以评估预测变量的重要性为例，借助随机森林的实现方法经常在文献中见到，例如下面的截图所示。先前也有好多同学咨询，说如何像这篇文献中这样，计算出预测变量的显著性？虽说最常使用的randomForest包可以给出预测变量的相对重要性得分，允许我们根据得分排名从中确定哪些预测变量是“更重要的”，但却没有提供估计p值的方法。当我们出于某种需要想获知变量的显著性信息时，仅使用randomForest包就会很困扰？

截图来自Jiao等（2018）的图5部分。左图展示了细菌、古细菌和真菌群落的α和β多样性在贡献深层土壤多养分循环指数中的重要性；右图展示了优势微生物分类群与土壤可利用钾的关系。两个图中变量的重要性以随机森林中的“percentage of increase of mean square error”（Increase in MSE(%)）值进行衡量，更高的MSE％值意味着更重要的变量，并标识了各变量的显著性。图上方的数值为总方差解释率，以及全模型的显著性p值。

randomForest包实现不了的功能，那就用其它R包进行补充呗。至于用哪些R包可以，文献中通常都有详细的方法描述，仔细看一下材料方法部分大致就明确了。就以上面的Jiao等（2018）的文章为例，材料方法部分提到可通过A3包可获取对全模型显著性的估计，并可通过rfPermute包可获取对随机森林中预测变量重要性的显著水平估计。

接下来，就简单展示A3包和rfPermute包的使用，包括如何使用这些包执行随机森林分析，以及获取对全模型或者重要预测变量的显著性的估计。

下文的测试数据，R代码等的百度盘链接（提取码，z8zb）：

https://pan.baidu.com/s/1-L78HuRzZCvH2LCzys4wJQ

若百度盘失效，也可在GitHub的备份中获取：

https://github.com/lyao222lll/sheng-xin-xiao-bai-yu

通过R包randomForest执行随机森林回归

为了进行对比说明，先来回顾一个先前的例子。

例如前文“随机森林回归”中使用R语言randomForest包执行随机森林回归。我们基于45个连续生长时间中植物根际土壤样本中细菌单元（OTU）的相对丰度数据，通过随机森林拟合了植物根际细菌OTU丰度与植物生长时期的响应关系（即，随机森林回归模型构建），根据植物根际细菌OTU丰度预测植物生长时期（即，通过预测变量对响应变量的值进行预测），并筛选出10个重要的具有明显时间特征的植物根际细菌OTU（即，评估预测变量的相对重要性并筛选重要的预测变量组合）。完整分析过程可参考前文“随机森林回归模型以及对重要变量的选择”，这里作了删减和改动，仅看其中的评估变量重要性的环节部分。

示例数据

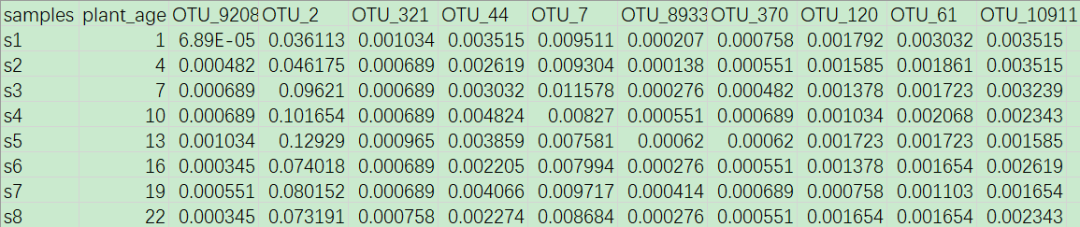
网盘示例数据“otu_top10.txt”中，共记录了45个连续生长时间中植物根际土壤样本中10种细菌OTU的相对丰度信息。

其中，samples列为45个样本的名称；plant_age记录了这45个根际土壤样本对应的植物生长时间（或称植物年龄），时间单位是天；其余10列为10种重要的细菌OTU的相对丰度信息，预先根据某些统计方法筛选出来的，它们已知与植物生长时间密切相关。

执行随机森林评估变量重要性

在这里，我们期望通过随机森林拟合这10种根际细菌OTU丰度与植物生长时期的响应关系，以得知哪些根际细菌OTU更能指示植物年龄。

#读取 OTU 丰度表

#包含预先选择好的 10 个重要的 OTU 相对丰度以及这 45 个根际土壤样本对应的植物生长时间（天）
otu <- read.delim('otu_top10.txt', row.names = 1)
 
##randomForest 包的随机森林
library(randomForest)
 
#随机森林计算（默认生成 500 棵树），详情 ?randomForest
set.seed(123)
otu_forest <- randomForest(plant_age~., data = otu, importance = TRUE, ntree = 500)
otu_forest
 
#使用函数 importance() 查看表示每个预测变量（细菌 OTU）重要性的得分（标准化后的得分）
importance_otu.scale <- data.frame(importance(otu_forest, scale = TRUE), check.names = FALSE)
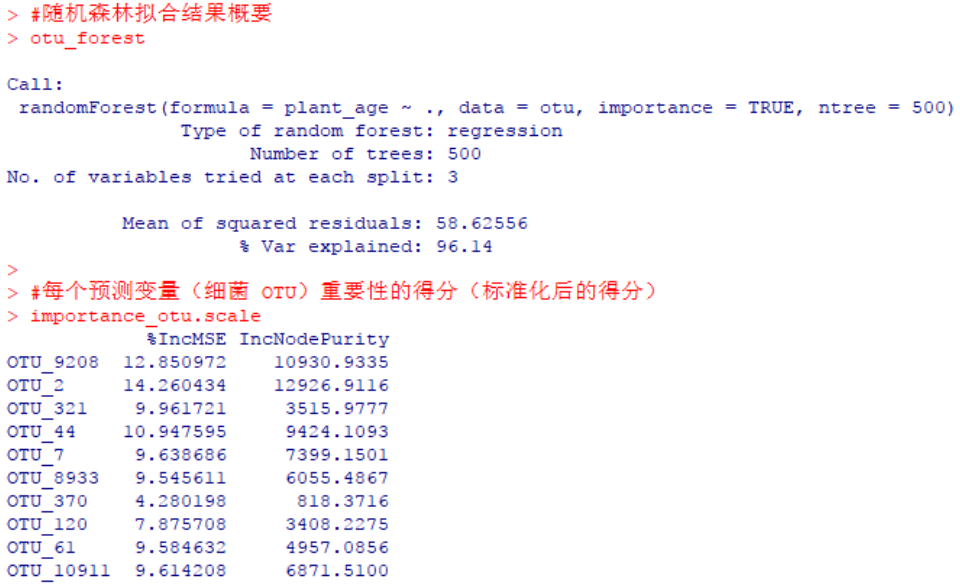
importance_otu.scale

如前所述，结果中“% Var explained”体现了预测变量（用于回归的10个细菌OTU）对响应变量（植物年龄）有关方差的整体解释率，这里为96.14%，反映了这个随机森林模型很高的拟合优度。

函数importance()给出了预测变量（10个细菌OTU）的相对重要性得分。“%IncMSE”即increase in mean squared error，通过对每一个预测变量随机赋值，如果该预测变量更为重要，那么其值被随机替换后模型预测的误差会增大。“IncNodePurity”即increase in node purity，通过残差平方和来度量，代表了每个变量对分类树每个节点上观测值的异质性的影响，从而比较变量的重要性。两个指示值均是判断预测变量重要性的指标，均是值越大表示该变量的重要性越大，但分别基于两者的重要性排名存在一定的差异。至于选择哪一个更合适，自己看着来吧。

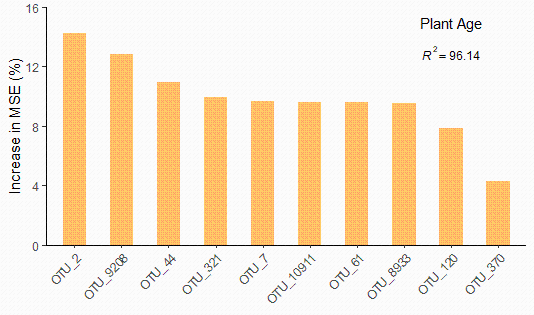
最后绘制柱形图观察和比较这些预测变量（10个细菌OTU）的相对重要性得分及排名。

#对预测变量（细菌 OTU）按重要性得分排个序，例如根据“%IncMSE”
importance_otu.scale <- importance_otu.scale[order(importance_otu.scale$'%IncMSE', decreasing = TRUE), ]
 
#简单地作图展示预测变量（细菌 OTU）的 %IncMSE 值
library(ggplot2)
 
importance_otu.scale$OTU_name <- rownames(importance_otu.scale)
importance_otu.scale$OTU_name <- factor(importance_otu.scale$OTU_name, levels = importance_otu.scale$OTU_name)
 
p <- ggplot(importance_otu.scale, aes(OTU_name, `%IncMSE`)) +
geom_col(width = 0.5, fill = '#FFC068', color = NA) +
labs(title = NULL, x = NULL, y = 'Increase in MSE (%)', fill = NULL) +
theme(panel.grid = element_blank(), panel.background = element_blank(), axis.line = element_line(colour = 'black')) +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
scale_y_continuous(expand = c(0, 0), limit = c(0, 16))
 
p
 
#右上角备注模型的已知解释率
p <- p +
annotate('text', label = 'Plant Age', x = 9, y = 15, size = 4) +
annotate('text', label = sprintf('italic(R^2) == %.2f', 96.14), x = 9, y = 13, size = 3, parse = TRUE)
 
p

通过rfPermute包执行随机森林回归以及获取变量的显著性

尽管上文randomForest包通过计算预测变量的相对重要性得分，允许我们根据得分排名从中确定预测变量的可靠程度，但没有告知我们这些变量是否是显著的。毕竟有些情况下我们确实想迫切知道变量的显著性，如Jiao等（2018）里的那样（本文开篇截图所示文献），因为这些统计量在这些情况中可能很有用。但由于randomForest()函数没有提供估计p值的方法（虽然它有个参数nPerm，但很可惜并不是计算p值的功能），就会很困扰。

仿照Jiao等（2018）的方法，我们可以使用rfPermute包的随机森林去评估每个预测变量（用于回归的10个细菌OTU）对响应变量（植物年龄）的重要性，并获得显著性信息。其实在使用过程中不难看出，rfPermute包沿用了randomForest包的随机森林方法，并对randomForest包的功能作了一些拓展。事实上，我们其实可以跳过randomForest包，直接通过rfPermute包对上文给定的数据执行随机森林分析，会得到和randomForest包一样的运行结果。然后rfPermute包的优势在于给出预测变量重要性得分的同时，还基于置换检验的原理对重要性得分进行了检验，并提供了显著性信息。

library(rfPermute)
#使用函数 rfPermut() 重新对上述数据执行随机森林分析，详情 ?rfPermut
#rfPermut() 封装了 randomForest() 的方法，因此在给定数据和运行参数一致的情况下，两个函数结果也是一致的
#并在这里额外通过 nrep 参数执行 1000 次的随机置换以评估变量显著性的 p 值
#若数据量较大，可通过 num.cores 参数设置多线程运算
set.seed(123)
otu_rfP <- rfPermute(plant_age~., data = otu, importance = TRUE, ntree = 500, nrep = 1000, num.cores = 1)
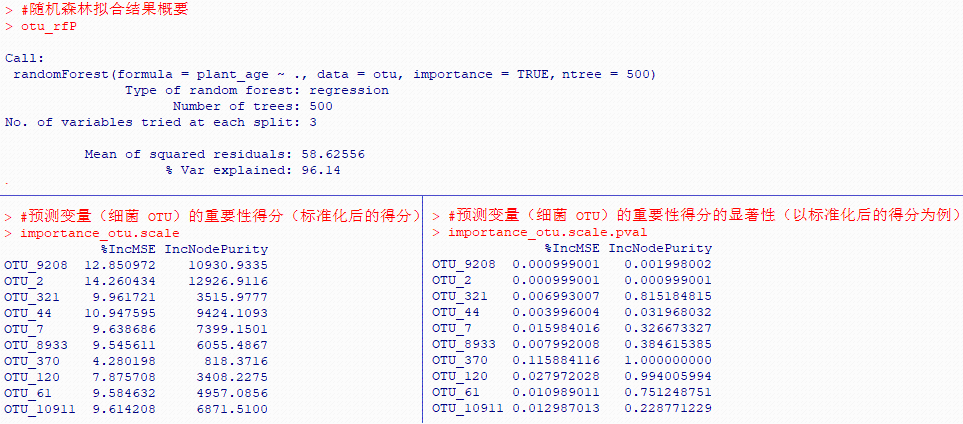
otu_rfP
 
#提取预测变量（细菌 OTU）的重要性得分（标准化后的得分）
importance_otu.scale <- data.frame(importance(otu_rfP, scale = TRUE), check.names = FALSE)
importance_otu.scale
 
#提取预测变量（细菌 OTU）的重要性得分的显著性（以标准化后的得分为例）
# summary(otu_rfP)
importance_otu.scale.pval <- (otu_rfP$pval)[ , , 2]
importance_otu.scale.pval

我们看到rfPermute()的结果中“% Var explained”为96.14%，和上文randomForest()的结果完全一致。但rfPermute()除了给出了预测变量（10个细菌OTU）的相对重要性得分“%IncMSE”和“IncNodePurity”外，还估计了得分的显著性信息，这是randomForest()所没有提供的。

类似地，基于两个指示值的重要性排名和显著性存在一定的差异，实际中二选一看着来。

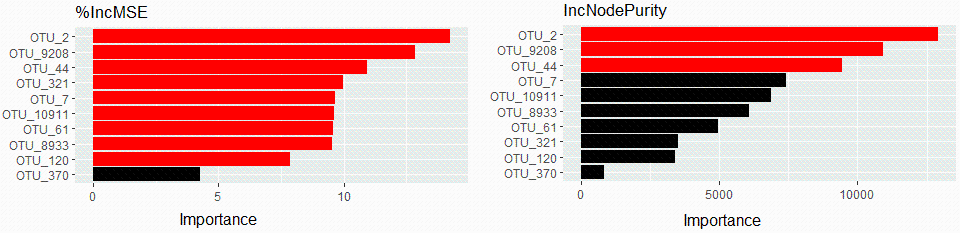
#作图展示预测变量（细菌 OTU）的重要性得分（标准化后的得分），其中显著的得分（默认 p<0.05）以红色显示
plot(rp.importance(otu_rfP, scale = TRUE))

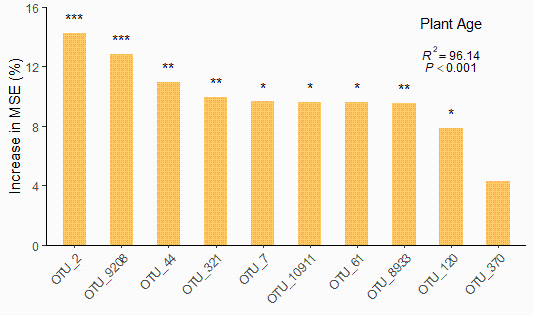
这次，我们即可将这些预测变量（10个细菌OTU）的显著性信息添加在上文的柱形图中，和它们的相对重要性得分及排名一起展示。

#对预测变量（细菌 OTU）按重要性得分排个序，例如根据“%IncMSE”
importance_otu.scale <- importance_otu.scale[order(importance_otu.scale$'%IncMSE', decreasing = TRUE), ]
 
#简单地作图展示预测变量（细菌 OTU）的 %IncMSE 值
library(ggplot2)
 
importance_otu.scale$OTU_name <- rownames(importance_otu.scale)
importance_otu.scale$OTU_name <- factor(importance_otu.scale$OTU_name, levels = importance_otu.scale$OTU_name)
 
p <- ggplot() +
geom_col(data = importance_otu.scale, aes(x = OTU_name, y = `%IncMSE`), width = 0.5, fill = '#FFC068', color = NA) +
labs(title = NULL, x = NULL, y = 'Increase in MSE (%)', fill = NULL) +
theme(panel.grid = element_blank(), panel.background = element_blank(), axis.line = element_line(colour = 'black')) +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
scale_y_continuous(expand = c(0, 0), limit = c(0, 16))
 
p
 
#标记预测变量（细菌 OTU）的显著性信息
#默认以 p<0.05 为 *，p<0.01 为 **，p<0.001 为 ***
for (OTU in rownames(importance_otu.scale)) {
    importance_otu.scale[OTU,'%IncMSE.pval'] <- importance_otu.scale.pval[OTU,'%IncMSE']
    if (importance_otu.scale[OTU,'%IncMSE.pval'] >= 0.05) importance_otu.scale[OTU,'%IncMSE.sig'] <- ''
    else if (importance_otu.scale[OTU,'%IncMSE.pval'] >= 0.01 & importance_otu.scale[OTU,'%IncMSE.pval'] < 0.05) importance_otu.scale[OTU,'%IncMSE.sig'] <- '*'
    else if (importance_otu.scale[OTU,'%IncMSE.pval'] >= 0.001 & importance_otu.scale[OTU,'%IncMSE.pval'] < 0.01) importance_otu.scale[OTU,'%IncMSE.sig'] <- '**'
    else if (importance_otu.scale[OTU,'%IncMSE.pval'] < 0.001) importance_otu.scale[OTU,'%IncMSE.sig'] <- '***'
}
 
p <- p +
geom_text(data = importance_otu.scale, aes(x = OTU_name, y = `%IncMSE`, label = `%IncMSE.sig`), nudge_y = 1)
 
p
 
#右上角备注模型的已知解释率
p <- p +
annotate('text', label = 'Plant Age', x = 9, y = 15, size = 4) +
annotate('text', label = sprintf('italic(R^2) == %.2f', 96.14), x = 9, y = 13, size = 3, parse = TRUE)
 
p

通过A3包获取全模型的显著性

另一方面，randomForest包虽然给出了全模型的方差解释率（即，R²），但也没有对全模型的显著性进行评估。不过与上述各个预测变量的p值相比，全模型的p值倒不是很纠结人，因为根据经验，只要R²不是特别小，p值都是绝对显著的。例如这里R²=0.9614，用眼睛就能直接判断出来p<0.001……当然话虽这样说，该计算的还是要计算一下。

同样仿照Jiao等（2018）的方法，我们可以使用A3包评估全模型的显著性。

library(A3)
#model.fn=randomForest 调用随机森林的方法进行运算
#p.acc=0.001 表示基于 1000 次随机置换获得对 p 值的估计，p.acc 值越小代表置换次数越多，运算也就越慢，因此如果对全模型 p 值不是很迫切的话还是慎用
#model.args 用于传递参数给 randomForest()，因此里面的参数项根据 randomForest() 的参数项而定，具体可 ?randomForest
#其它详情可 ?a3 查看帮助 
set.seed(123)
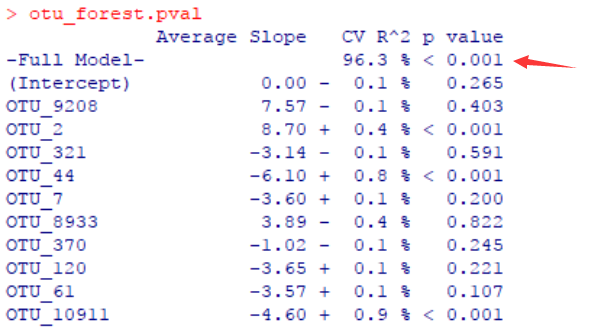
otu_forest.pval <- a3(plant_age~., data = otu, model.fn = randomForest, p.acc = 0.001, model.args = list(importance = TRUE, ntree = 500))
otu_forest.pval

我们看到全模型的p<0.001是非常显著的。由于随机的因素在里面，这里的R²和上文的R²相比有很微小的差异，但是并无大碍，就默认为它们一致就可以了。至于结果中的其它值反映了什么信息，我没有过多关注，大家有兴趣可以自己研究下。

其它缺点是这一步非常耗时，貌似还不能多线程，因此大数据慎用……

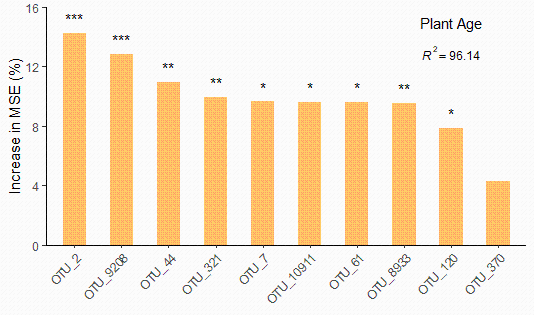
最后，我们再将全模型的显著性信息备注在上文的柱形图中，和全模型的方差解释率、预测变量（10个细菌OTU）的相对重要性得分、排名以及显著性信息一起展示。

#继续在右上角备注全模型的显著性信息
p <- p +
annotate('text', label = sprintf('italic(P) < %.3f', 0.001), x = 9, y = 12, size = 3, parse = TRUE)
 
p

参考资料

Jiao S, Chen W, Wang J, et al. Soil microbiomes with distinct assemblies through vertical soil profiles drive the cycling of multiple nutrients in reforested ecosystems. Microbiome, 2018, 6(1): 1-13.

rfPermute包：https://www.rdocumentation.org/packages/rfPermute/versions/2.1.81

A3包：https://rdrr.io/cran/A3/

友情链接

关于多元回归中需考虑的问题：

变量选择

多重共线性

一般线性模型（LM）：

简单线性回归和多次项回归

多元线性回归（MLR）

带有类别型自变量的线性回归

广义线性模型（GLM）：

计数型响应变量：泊松回归负二项回归

类别型响应变量：logistic回归

比例型响应变量：beta回归

常见的非线性模型：

带交互效应的多元回归

指数回归和线性变换求解

平滑拟合，局部加权回归（LOESS）

一般加性模型和广义加性模型（GAM）

分段线性回归及对分段断点的评估

回归树：

随机森林（RF）

Aggregated boosted tree（ABT）

多元回归树（MRT）

生存分析：

非参数方法（Kaplan-Meier曲线）

半参数生存回归（Cox回归）

参数生存回归

基于相似或相异矩阵的回归或降维思想的回归：

基于相似或相异矩阵的多元回归（MRM）

基于成分或特征的回归

偏最小二乘（PLS）回归

冗余分析（RDA）主响应曲线（PRC）

典范对应分析（CCA）

基于距离的冗余分析（db-RDA），或称典范主坐标分析（CAP）

结构方程模型（SEM）：

路径分析

验证性因子分析（CFA）

潜变量结构模型

分段结构方程建模

猜你喜欢

10000+：菌群分析宝宝与猫狗梅毒狂想曲提DNA发Nature Cell专刊肠道指挥大脑

系列教程：微生物组入门 Biostar 微生物组宏基因组

专业技能：学术图表高分文章生信宝典不可或缺的人

一文读懂：宏基因组寄生虫益处进化树

必备技能：提问搜索 Endnote

文献阅读热心肠 SemanticScholar Geenmedical

扩增子分析：图表解读分析流程统计绘图

16S功能预测 PICRUSt FAPROTAX Bugbase Tax4Fun

在线工具：16S预测培养基生信绘图

科研经验：云笔记云协作公众号

编程模板: Shell R Perl

生物科普: 肠道细菌人体上的生命生命大跃进细胞暗战人体奥秘

写在后面

为鼓励读者交流、快速解决科研困难，我们建立了“宏基因组”专业讨论群，目前己有国内外5000+ 一线科研人员加入。参与讨论，获得专业解答，欢迎分享此文至朋友圈，并扫码加主编好友带你入群，务必备注“姓名-单位-研究方向-职称/年级”。PI请明示身份，另有海内外微生物相关PI群供大佬合作交流。技术问题寻求帮助，首先阅读《如何优雅的提问》学习解决问题思路，仍未解决群内讨论，问题不私聊，帮助同行。