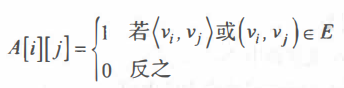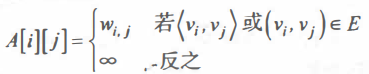数据结构 (五) – 图
= LUOFANG SHIJIE + 网上的小伙伴见解 + 个人见解
侵删!
“首当其冲”
在有向图中,顶点用尖括号,在无向图中,顶点用圆括号
例如<x,y>和<y,x>是不相同的,但是(x,y)和(y,x)是相同的。
在图中,一般用n来表示顶点的数目,用e来表示边的数目
无向完全图和有向完全图:
无向完全图:边的数目为n(n-1)/2
有向完全图:边的数目为n(n-1)
网:带权的图往往称为网
入度和出度:对于有向图而言的。在有向图中,所有顶点的入度和出度之和的1/2为图的边数
路径长度:是一条路径上通过边的条数
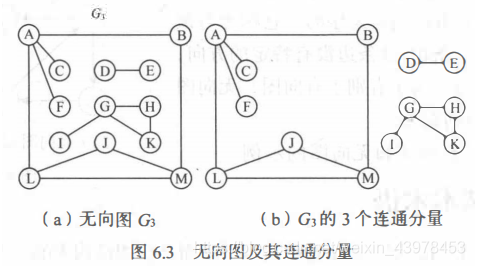
连通、连通图、连通分量:有路径——连通 在图中,任一顶点都有路径——连通图
无向图中的极大连通子图——连通分量
强连通图和强连通分量:是相对于有向图而言的。
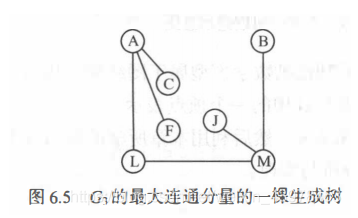
连通图的生成树:一个极小连通子图,他包含图中的所有顶点,但是只有足以构成一棵树的n-1条边。
如果一个图有n个顶点和小于n-1条边,那一定是非连通图,如果他多于n-1条边,那一定有环。
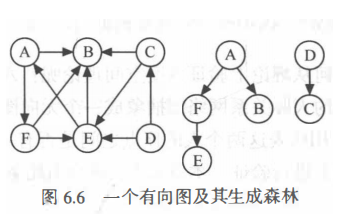
有向树和生成森林:只有一个点的入度为0,其余点的入度均为1的有向图称为有向树
生成森林:由若干棵有向树组成,且互不相交
图的存储结构
邻接矩阵表示法
若图是网,则可以这样表示:
#define MaxInt 32767
#define MVNum 100
typedef char VerTexType; //假设顶点的类型是char型
typedef int ArcType; //假设边的权值类型是int
typedef struct
{
VerTexType vexs[MVNum];
ArcTexType arcs[MVNum][MVNum];
int arcnum,vexnum;
}AMGraph;
采用邻接矩阵法创建无向网:时间复杂度0(n2)
Status CreatUND(AMGraph &G)
{
cin>>G.arcnum>>G.vexnum;
for(int i=0;i<vexnum;i++) //依次输入顶点信息
cin>>G.vexs[i];
for(int i=0;i<vexnum;i++)
{
for(int j=0;j<vexnum;j++)
{
G.arcs[i][j]=MaxInt;
}
}
for(int k=0;k<G.arcnum;k++)
{
cin>>v1>>v2>>w; //输入一条边依附的顶点和权值
i=LocateVex(G,v1);
j=LocateVex(G,v2);
G.arcs[i][j]=w;
G.arcs[i][j]=G.arcs[j][i]; //无向网
}
return OK;
}
对于边数相对顶点较少的图,这种结构是存在对存储空间的极大浪费的。因此我们考虑另外一种存储结构方式:邻接表(Adjacency List),即数组与链表相结合的存储方法。
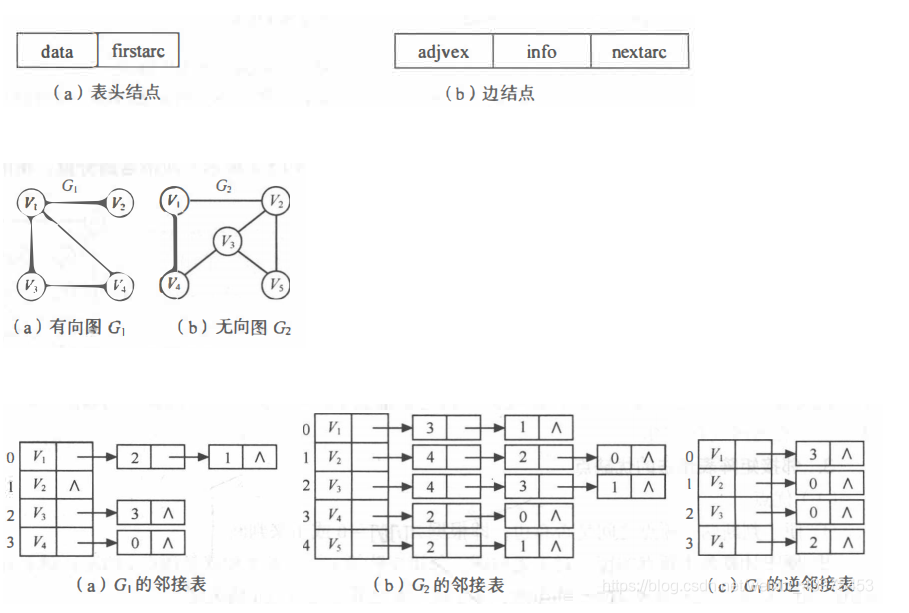
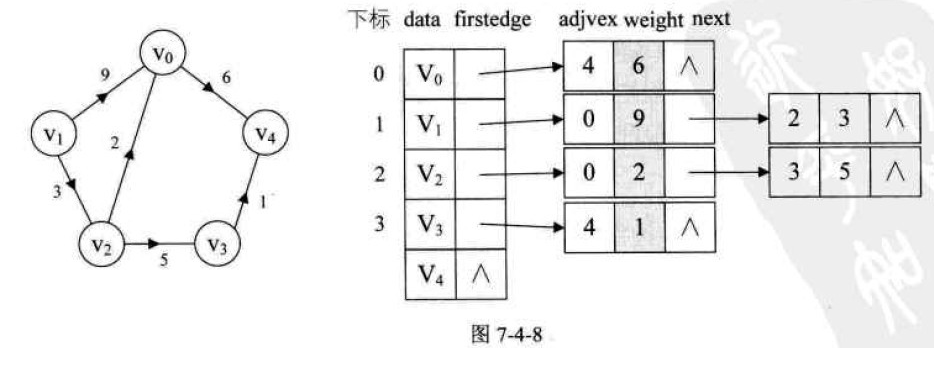
邻接表表示法
课本的理解有点混
new:
-
图中顶点用一个一维数组存储,另外,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
-
图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点vi的边表,有向图称为顶点vi作为弧尾的出边表。
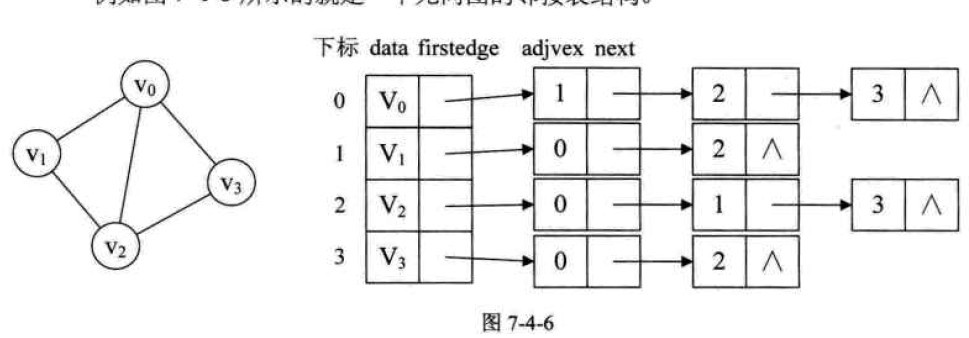
无向图的邻接表结构。
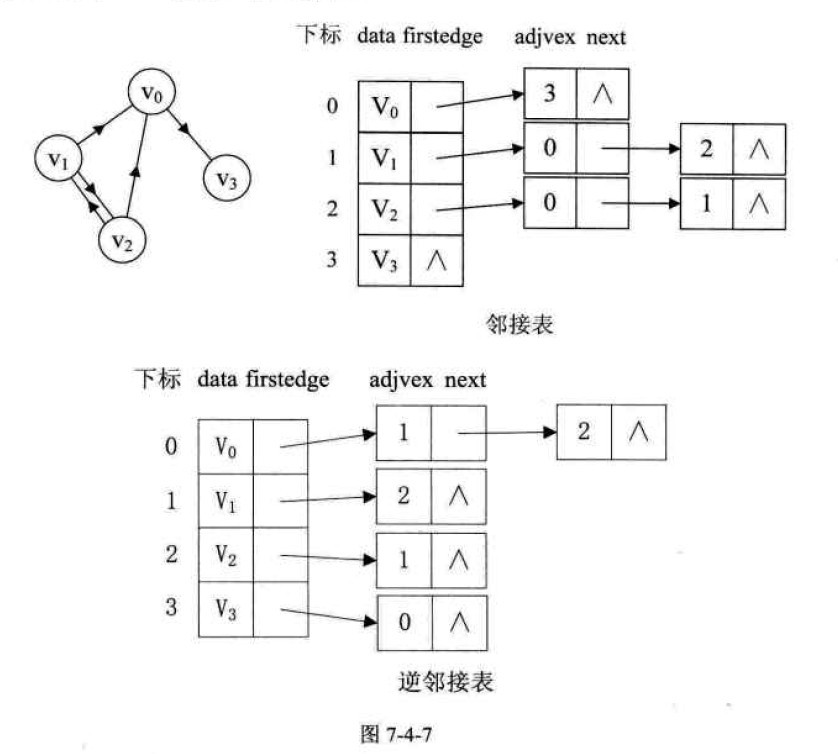
若是有向图,邻接表的结构是类似的
如图以顶点作为弧尾来存储边表容易得到每个顶点的出度,而以顶点为弧头的表容易得到顶点的入度,即逆邻接表。
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可
图的遍历
两种遍历方法:
深度优先搜索 和 广度优先搜索
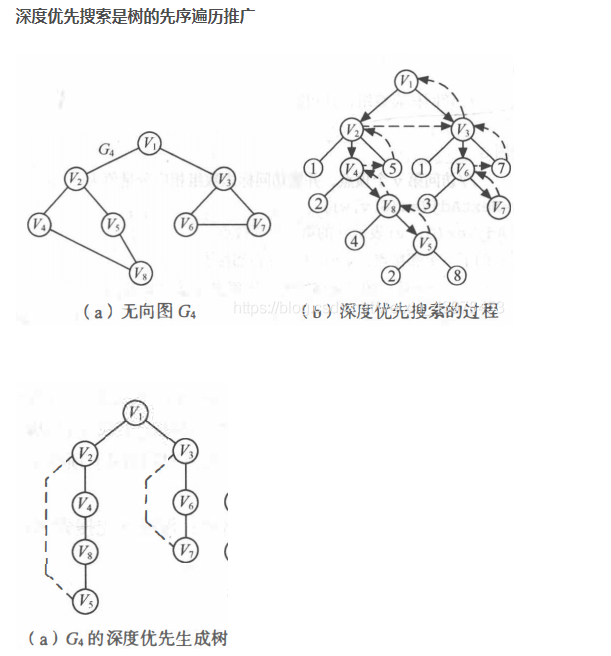
深度优先搜索
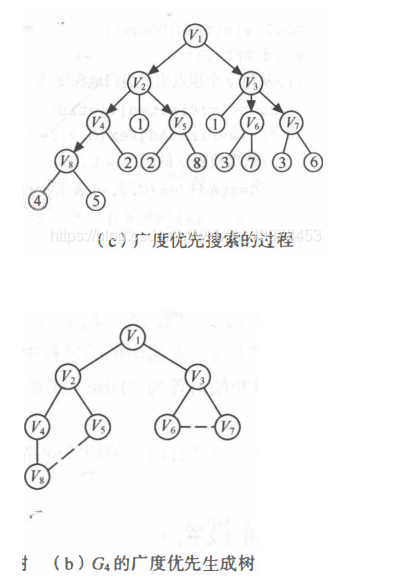
广度优先搜索类似于树的层次遍历
广度优先算法需要用到队列
算法分析:广度优先算法和深度优先算法时间复杂度是一样的,他们都取决于查找邻接点的复杂度
图的应用
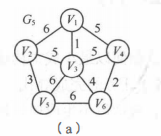
最小生成树
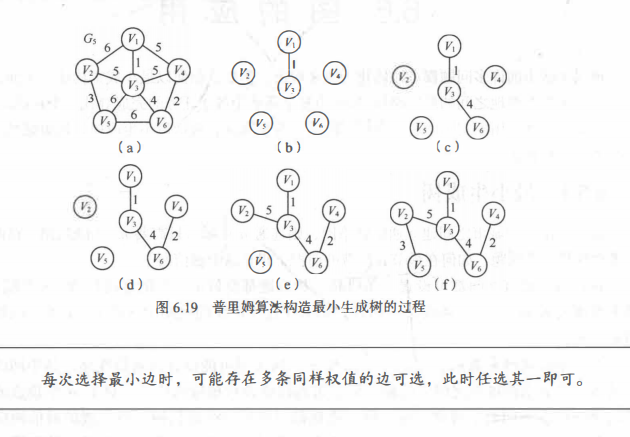
普里姆算法
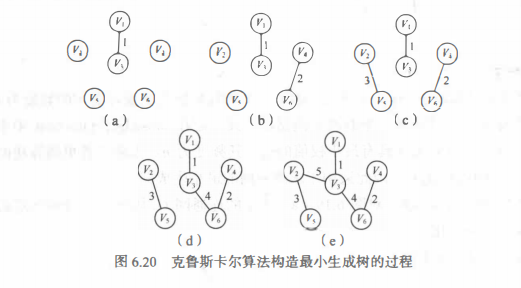
克鲁斯卡尔算法
今天的文章数据结构,图_数据结构无向图「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/65597.html