java 递归 + java合并算法

前言

本来标题应该是“python 如何下载wordcloud；python 如何下载lxml；python如何下载pyHook；python如何下载dlib”。但是，我懒了。毕竟已经写好了这个文章，那么就不写python的了。

当一个合格的鸽子精才是我的人生追求（bushi

下面进入正题：

什么是递归？

递归是一个方法调用自身的过程。（没了，就这。）

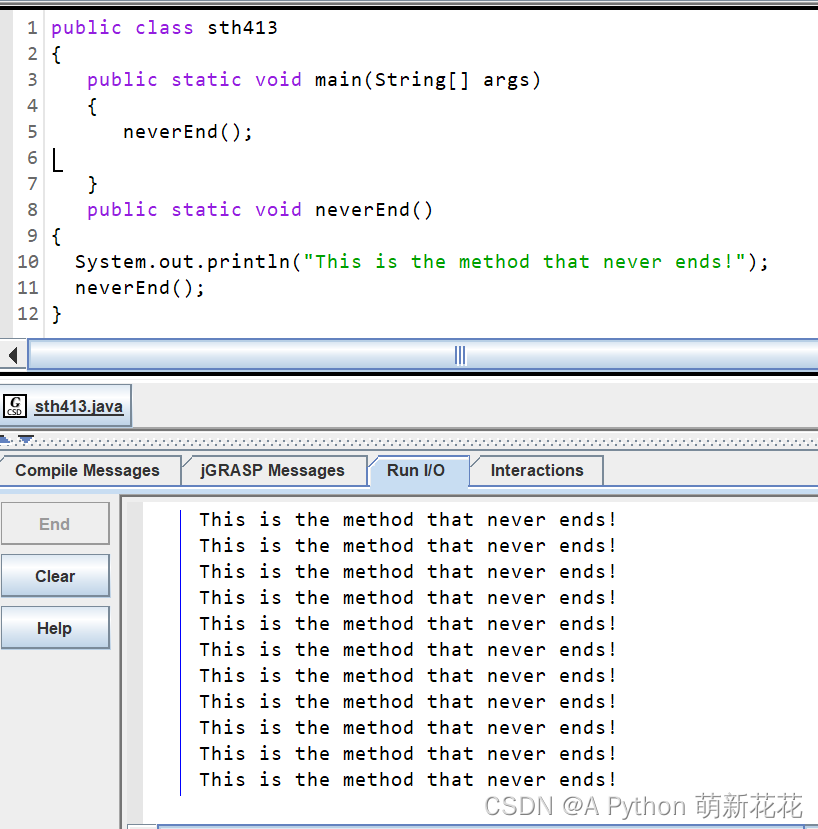
让我们来看个例子：

public static void neverEnd()
{
  System.out.println("This is the method that never ends!");
  neverEnd();
}

就是一个很直观的感觉。

这个neverEnd方法不断地调用了自己。执行过程大概是：neverEnd方法调用 — 进入neverEnd方法 — 运行println — 再次调用neverEnd方法 — 运行println — 再次。。。。。

就这样，这个neverEnd方法在自身运行的时候不断调用了自己，创造出了一种无限循环的效果。

 递归的要素

例子1

public static int mystery()
{
   int total = 0;
   for (int i=10; i>0; i--)
   {
      total = total + i;
   }
   return total;
}

这个mystery方法用到了递归么？当然没有啦。

仔细一看的话，是可以发现：虽然这个mystery方法有着一个return的值，看起来很像递归，但是它其实不是，因为递归是一个调用自身的过程。很明显，这个方法里面并没有任何地方调用了这个mystery方法。

注：for循环可以是迭代，可以是遍历，但是绝对不会在单独出现的时候是递归。

单独的for ≠ 递归

例子2

public static int mystery2(int x)
{
   if (x == 1) return 1;
   else return x + mystery2(x-1);
}

那么这个mystery2方法用到了递归么？当然啦。

这个函数在x不等于1的时候，会返回一个值，就是x+mystery2(x-1)。在这个返回值中，这个函数调用了自身，使得这个方法出现了递归。

这个递归的过程大致是这个样的，假设x=4

调用mystery2方法，传参为4 — if判断，x不等于1 — 返回 4+mystery2（x-1 =3）– 调用mystery2方法，传参为3 — if判断，x不等于1 — 返回 3+mystery2（x-1 =2）– 调用mystery2方法，传参为2 — if判断，x不等于1 — 返回 2+mystery2（x-1 =1）– 调用mystery2方法，传参为1 — if判断，x等于1 — 返回 1 — 方法为1并没有递归，递归结束，返回最后的值。

这里面，最后的值就是 4 + 3 + 2 + 1 = 10

相当于：

4 + mystery2(3) = 4 + 3 + mystery2(2) = 4 + 3 + 2 + mystery2(1) = 4 + 3 + 2 + 1 = 10

总结

递归听起来很复杂，对吧。但是其实递归并没有想象中的那么复杂。

递归的要素主要就是一个，也就是它的定义：只有一个方法调用了它本体，这个方法才使用了递归。

只要将递归拆开一点点分析，画一下流程图，递归就被解决了。

为什么要用递归？

当递归用于解决问题结构重复的问题时，它最有用。例如，如果您想知道计算机上的文件夹使用了多少空间，该怎么办？您可以将该文件夹中所有文件的大小相加，但文件夹也可以包含子文件夹。因此，您必须对每个子文件夹重复该过程（方法）。每个子文件夹也可以包含子文件夹。
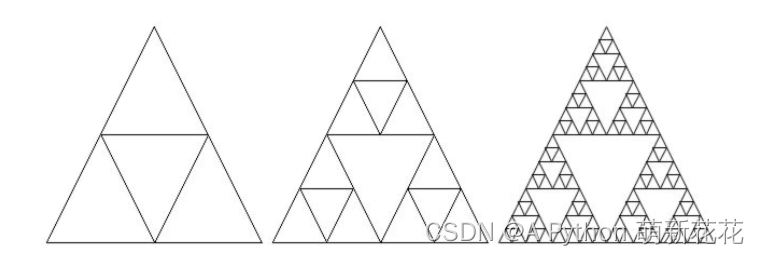
递归也可用于创建分形。一个简单的例子是Sierpinski的三角形，你可以将一个三角形细分为4个新的三角形，如下所示。然后，你可以对每个新的三角形（除了中心三角形）执行一些程序。

PS：这里偷偷推荐一下我上传的资源，是turtle库的扩展，大幅的减少了图形绘画的代码长度。 

递归也可以用于遍历字符串、数组和ArrayList对象，就像循环一样。事实上，任何递归解决方案都可以用迭代（循环）代替。

常见递归

阶乘

public class FactorialTest
{

    public static int factorial(int n)
    {
        if (n == 0)
            return 1;
        else
            return n * factorial(n-1);
    }

    public static void main(String[] args)
    {
        System.out.println("factorial of 3 is: " + factorial(3));
        System.out.println("factorial of 4 is: " +factorial(4));
        System.out.println("factorial of 5 is: " +factorial(5));
    }
}

 可以看到，这个factorial方法在return的时候调用了他自己。这个递归的使用跟前面的mystery2方法基本类似，不过这个factorial方法使用了乘法而不是加法。

factorial(5) 就相当于 5*4*3*2*1*1。有一点要注意就是这里面让递归停止的值是0而不是1。这个在阶乘里面可以用，因为都是乘法，乘1基本等于没乘。但是在上面的mystery2方法中就得是1了，因为如果是0的话，就会多加一个1。（除非改代码）

斐波那契数列

public class Fibonaqie {
    public static int feibonaqie(int number)
    {
        if (number==0||number==1)
        {
            return number;
        }
        else
        {
            return feibonaqie(number-1)+feibonaqie(number-2);
        }
    }
    public static void main(String args[])
    {
        int number = 3;
        System.out.println("第"+number+"项的斐波那锲值为："+feibonaqie(number));
    }
}

如果说到递归的话，程序员的第一反应绝对是斐波那契数列。可能别人看着斐波那契数列不觉得有啥，但是斐波那契数列本身的特性就是第n项等于第n-1项和第n-2项之和。这种感觉特别的像“想要知道a，就得先知道a-1；想要知道a-1，就得先知道a-2”。

虽然说斐波那契数列正向也能通过循环来算出来。不过要是说到代码简洁度的话，递归才是最好的选择。

递归的基本解（base case）

每个递归方法必须至少有一个停止递归的基本情况。这通常是一个if语句，它只需给出一个答案，而不需要递归方法调用，就可以停止递归。你也可以把它看作是最简单的情况，你可以马上给出答案。阶乘方法有一种停止递归（而不是调用自身）的方法。当n等于0时，它停止，因为它只返回1。这是基本情况。

一些案例

public static int factorial(int n)
{
    if (n == 0)
        return 1;
    else
        return n * factorial(n-1);
}

public static int product(int n)
{
   if(n == 1)
      return 1;
   else
      return n * product(n - 2);
}

public static int bunnyEars(int bunnies)
{
   if (bunnies == 0) return 0;
   else if (bunnies == 1) return 2;
   else return 2 + bunnyEars(bunnies - 1);
}

合并算法 — 递归

二进制搜索

非递归版

线性搜索通过按顺序检查每个元素来搜索数组或ArrayList中的元素。二进制搜索效率更高（更快），因为它从排序数组或ArrayList的中间开始，每次通过算法时都会消除一半数组或ArrayList。二进制搜索只对已排序的数据有效。它可以像下面这样通过迭代（使用循环）编写，也可以递归编写。

public class IterativeBinarySearch
{
   public static int binarySearch(int[] elements, int target) {
      int left = 0;
      int right = elements.length - 1;
      while (left <= right)
      {
         int middle = (left + right) / 2;
         if (target < elements[middle])
         {
            right = middle - 1;
         }
         else if (target > elements[middle])
         {
            left = middle + 1;
         }
         else {
            return middle;
         }
       }
       return -1;
   }

   public static void main(String[] args)
   {
      int[] arr1 = {-20, 3, 15, 81, 432};

      int index = binarySearch(arr1,81);
      System.out.println(index);
   }
}

递归版

public class RecursiveBinarySearch
{
  public static int recursiveBinarySearch(int[] array, int start, int end, int target)
  {
      int middle = (start + end)/2;
      // base case: check middle element
      if (target == array[middle]) {
          return middle;
      }
      // base case: check if we've run out of elements
      if(end < start){
          return -1; // not found
      }
      // recursive call: search start to middle
      if (target < array[middle]){
          return recursiveBinarySearch(array, start, middle - 1, target);
      }
      // recursive call: search middle to end
      if (target > array[middle]){
          return recursiveBinarySearch(array, middle + 1, end, target);
      }
      return -1;
  }

 public static void main(String[] args)
 {
    int[] array = { 3, 7, 12, 19, 22, 25, 29, 30 };
    int target = 25;
    int foundIndex = recursiveBinarySearch(array, 0, array.length-1, target);
    System.out.println(target + " was found at index " + foundIndex);
 }
}

合并算法

合并排序递归地将要排序的值一分为二，直到只有一个值要排序，然后将两个已排序列表合并为一个已排序列表。下面显示的代码使用与原始数组大小相同的第二个数组按顺序合并值。然后将所有排序的值复制回原始数组。

import java.util.Arrays;

public class SortTest
{
   public static void mergeSort(int[] elements)
   {
      int n = elements.length;
      int[] temp = new int[n];
      mergeSortHelper(elements, 0, n - 1, temp);
   }

   private static void mergeSortHelper(int[] elements,
                                       int from, int to, int[] temp)
   {
       if (from < to)
       {
          int middle = (from + to) / 2;
          mergeSortHelper(elements, from, middle, temp);
          mergeSortHelper(elements, middle + 1, to, temp);
          merge(elements, from, middle, to, temp);
       }
   }

   private static void merge(int[] elements, int from,
                             int mid, int to, int[] temp)
   {
      int i = from;
      int j = mid + 1;
      int k = from;

      while (i <= mid && j <= to)
      {
         if (elements[i] < elements[j])
         {
            temp[k] = elements[i];
            i++;
         }
         else
         {
            temp[k] = elements[j];
            j++;
         }
         k++;
      }

      while (i <= mid)
      {
         temp[k] = elements[i];
         i++;
         k++;
      }

      while (j <= to)
      {
         temp[k] = elements[j];
         j++;
         k++;
      }

      for (k = from; k <= to; k++)
      {
         elements[k] = temp[k];
      }
   }

   public static void main(String[] args)
   {
      int[] arr1 = {86, 3, 43, 5};
      System.out.println(Arrays.toString(arr1));
      mergeSort(arr1);
      System.out.println(Arrays.toString(arr1));
   }
}

今天的文章java 递归 + java合并算法分享到此就结束了，感谢您的阅读。