离线强化学习(Offline RL)系列3: (算法篇)策略约束 – BRAC算法原理详解与实现(经验篇)

论文原文：【Yifan Wu, George Tucker, Ofir Nachum: “Behavior Regularized Offline Reinforcement Learning”, 2019; arXiv:1911.11361】

本文是CMU和Google Research一起合作于2019年提出并发表在ICLR会议上，是一篇广泛的研究了BCQ和BEAR两个算法的优劣之后总结性工作，算法全称： Behavior Regularized ActorCritic (BRAC)（有点综述实验的味道，和之前的Deep reinforcement learning that matters很像）

摘要：BCQ算法通过添加VAE和扰动网络使得学习策略尽可能的靠近行为策略，BEAR算法提出来支撑集进一步优化学习策略，两者的相同点是都用了 ensemble Q-value函数，其中 BCQ的 $k=2$, BEAR 的 $k=4$，另外他们都使用了regularized learned policy来解决一些un-seen的state-action对(OOD)。
本文作者通过VP（value penalty）和PR（policy regularization 两种方式来提高算法的效率。并在此技术上讨论了诸如regularization weight、Divergence for regularization以及超参数选择等6方面的内容，论文做了大量的实验（一如既往的Google风格），结论是： （1）加权目标Q值集合和自适应正则化系数是不必要的；（2）价值惩罚（VP）的使用略优于策略正则化（PR），而许多可能的分歧(KL，MMD，Wass Dis)可以达到类似的性能。也许在这些离线设置中最重要的区别是是否使用了适当的超参数。

2. BRAC方法

作者首先回顾了BCQ和BEAR两种算法，其中BEAR算法使用了软更新的方式防止过估计(overestimate)问题（这里的 ${\psi }_j^{\prime }$ 表示目标Q函数的软更新集合， $k=4$）

$$\bar{Q}\left(s^{\prime },a^{\prime }\right):=0.75\cdot \underset{j=1,\dots ,k}{\min }{Q}_{{\psi }_j^{\prime }}\left(s^{\prime },a^{\prime }\right)+0.25\cdot \underset{j=1,\dots ,k}{\max }{Q}_{{\psi }_j^{\prime }}\left(s^{\prime },a^{\prime }\right)$$

另外分析了BCQ更新学习策略的过程如下：

$${\pi }_{\theta }(a\mid s):=\underset{a_i+{\xi }_{\theta }\left(s,a_i\right)}{\mathrm{argmax}}{Q}_{\psi }\left(s,a_i+{\xi }_{\theta }\left(s,a_i\right)\right)\text{ for }{a}_i\sim {\pi }_b(a\mid s),i=1,\dots ,N$$

2.1 两种方法

2.1.1 value penalty (VP)

作者提出了一个对值函数添加惩罚(penalty)项 $\alpha D(\pi (\cdot |s_t),{\pi }_b(\cdot |s_t))$ 作为对策略的penalty,计算过程如下：

$$V_D^{\pi }(s)=\sum _{t=0}^{\infty }{\gamma }^t{\mathbb{E}}_{s_t\sim P_t^{\pi }(s)}\left[R^{\pi }\left(s_t\right)-\alpha D\left(\pi \left(\cdot \mid s_t\right),{\pi }_b\left(\cdot \mid s_t\right)\right)\right]$$

可以清楚看到，和普通的算法的区别就在这个惩罚项上，有那么点baseline的感觉，作者也在这里强调了当使用single-sample estimate的时候等价于SAC算法。

2.1.2 policy regularization(PR)

这部分和VP的计算方式一样，不同点在于公式中的 $\alpha$：

• if $\alpha =0$, Q函数更新
• else $\alpha \ne 0$. policy更新
  

2.2 四种度量方法

下面四种度量方式都是去计算两个分布之间的距离或者说衡量两个分布是否一致的方法，其中Kernel MMD在BEAR算法中使用过，KL在TRPO、PPO、BCQ等很多算法中使用过，Wasserstein在分布强化学习（A Distributional perspective of Reinforcement Learning）中使用过，此处不在一一详解。

2.2.1 Kernel MMD

MMD ⁡ 2 ( { x 1 , ⋯   , x n } , { y 1 , ⋯   , y m } ) = 1 n 2 ∑ i , i ′ k ( x i , x i ′ ) − 2 n m ∑ i , j k ( x i , y j ) + 1 m 2 ∑ j , j ′ k ( y j , y j ′ ) \operatorname{MMD}^{2}\left(\left\{x_{1}, \cdots, x_{n}\right\},\left\{y_{1}, \cdots, y_{m}\right\}\right)=\frac{1}{n^{2}} \sum_{i, i^{\prime}} k\left(x_{i}, x_{i^{\prime}}\right)-\frac{2}{n m} \sum_{i, j} k\left(x_{i}, y_{j}\right)+\frac{1}{m^{2}} \sum_{j, j^{\prime}} k\left(y_{j}, y_{j^{\prime}}\right) MMD2({
x1​,⋯,xn​},{
y1​,⋯,ym​})=n21​i,i′∑​k(xi​,xi′​)−nm2​i,j∑​k(xi​,yj​)+m21​j,j′∑​k(yj​,yj′​)

2.2.2 KL-Divergence

$$D_{\mathrm{K}\mathrm{L}}\left({\pi }_{\theta }(\cdot \mid s),{\pi }_b(\cdot \mid s)\right)={\mathbb{E}}_{a\sim {\pi }_{\theta }(\cdot \mid s)}\left[\log {\pi }_{\theta }(a\mid s)-\log {\pi }_b(a\mid s)\right]$$

2.2.3 f-divergence

$$D_f(p,q)={\mathbb{E}}_{x\sim p}[f(q(x)/p(x))]=\underset{g:\mathcal{X}\mapsto \mathrm{dom}\left(f^{\ast }\right)}{\max }{\mathbb{E}}_{x\sim q}[g(x)]-{\mathbb{E}}_{x\sim p}\left[f^{\ast }(g(x))\right]$$

2.2.4 Wasserstein Distance（WD）

$$W(p,q)=\underset{g:\Vert g{\Vert }_L\le 1}{\sup }{\mathbb{E}}_{x\sim p}[g(x)]-{\mathbb{E}}_{x\sim q}[g(x)]$$

3. 实验过程及分析（很关键的内容）

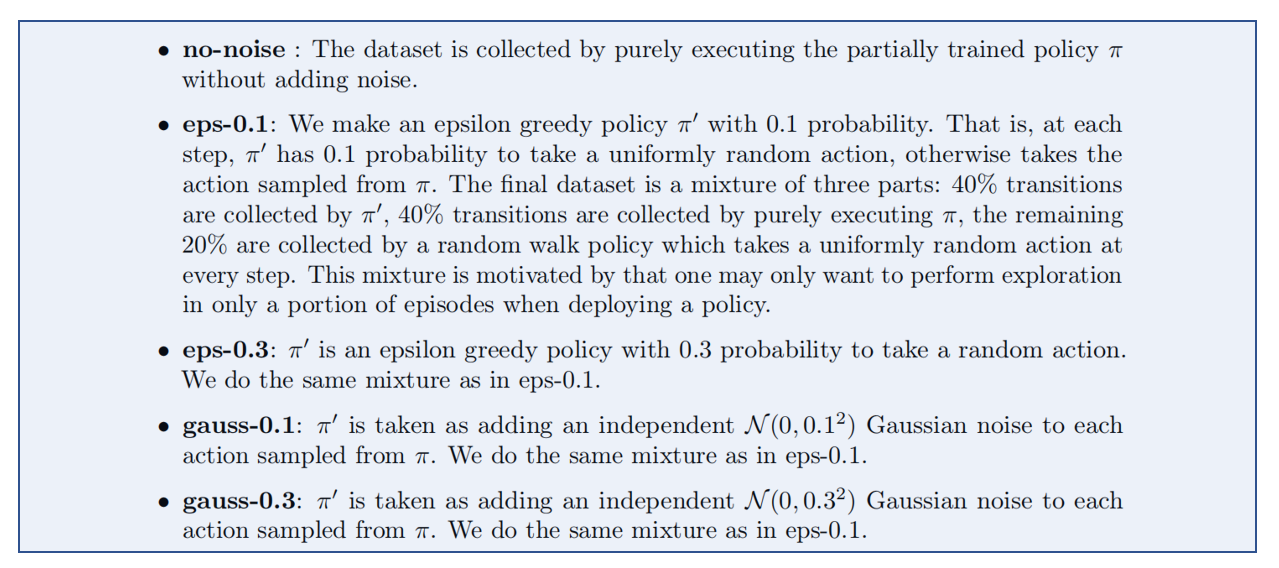
实验之前，我们先说一下实验进行的dataset问题，作者通过添加不同的noise生成5类数据集，分别如下：

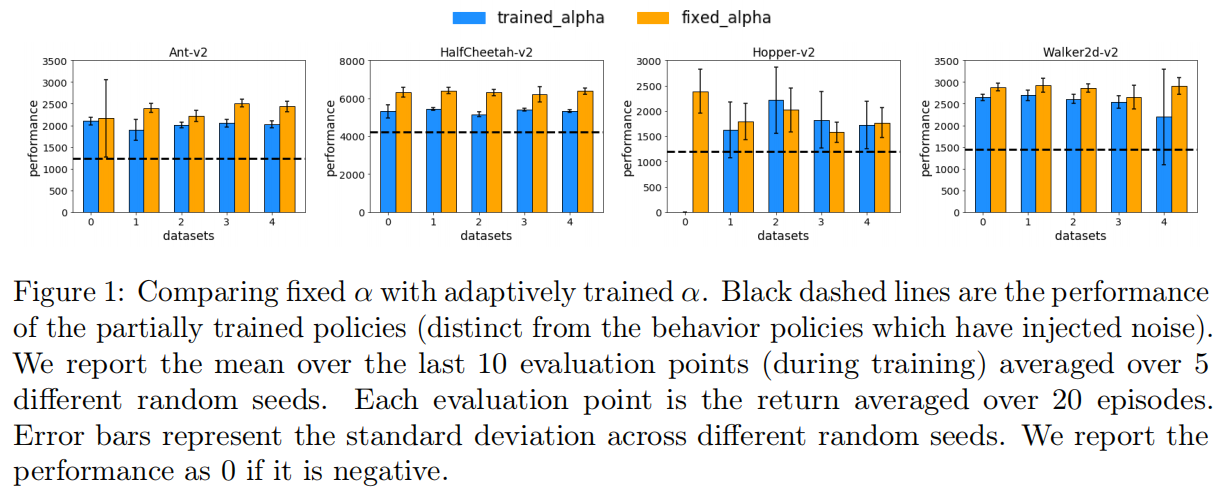
3.1 固定&自适应regularization weights

发现： 当BEAR使用 $\epsilon$ 的推荐值时，$\alpha$ 的学习值在训练过程中持续增加，这意味着 ${\pi }_{\theta }$ 和 ${\pi }_b$ 之间的MMD约束几乎从不得到满足。表明BEAR有效地执行了具有大$\alpha$ 的策略正则化，而不是约束优化。
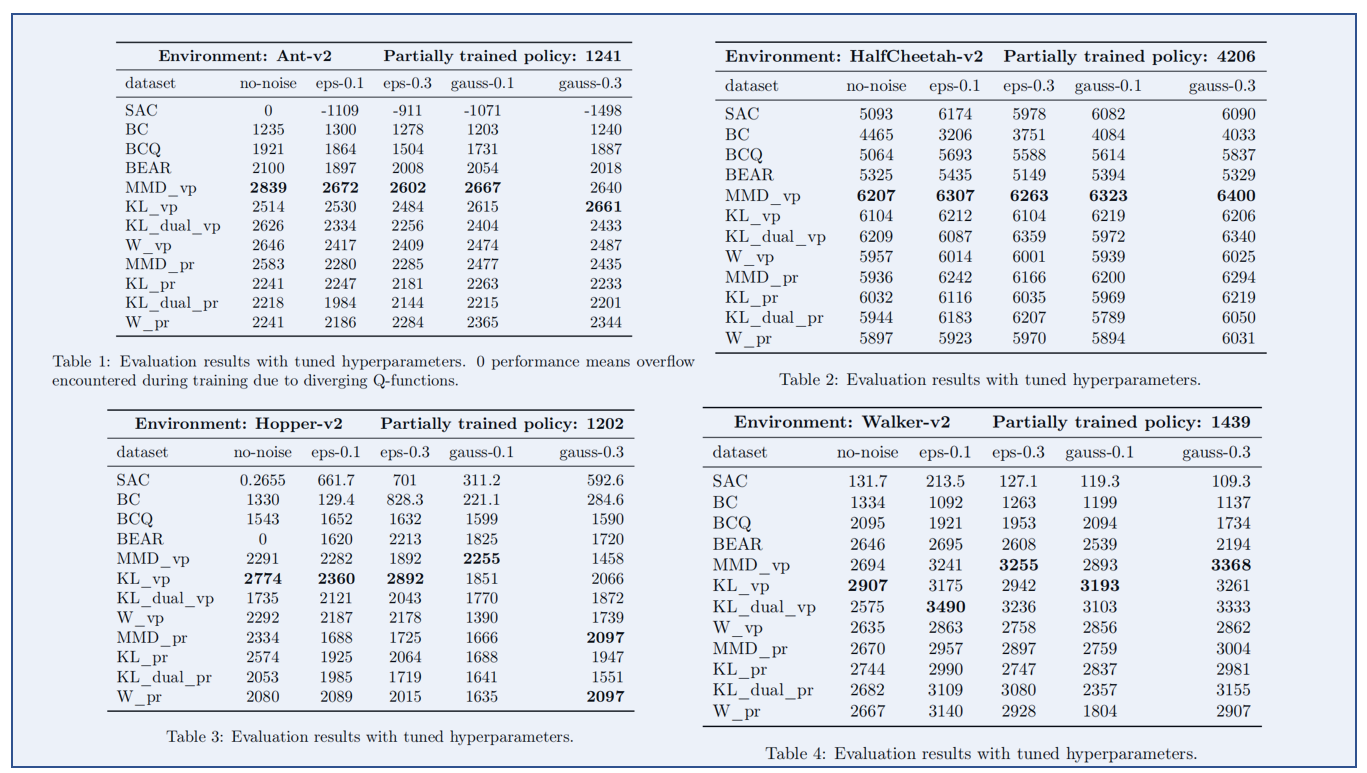
结论：自适应和固定的 $\alpha$ 都比partially trained policy效果要好， 图中的黑色线是行为策略未注入噪音的结果。

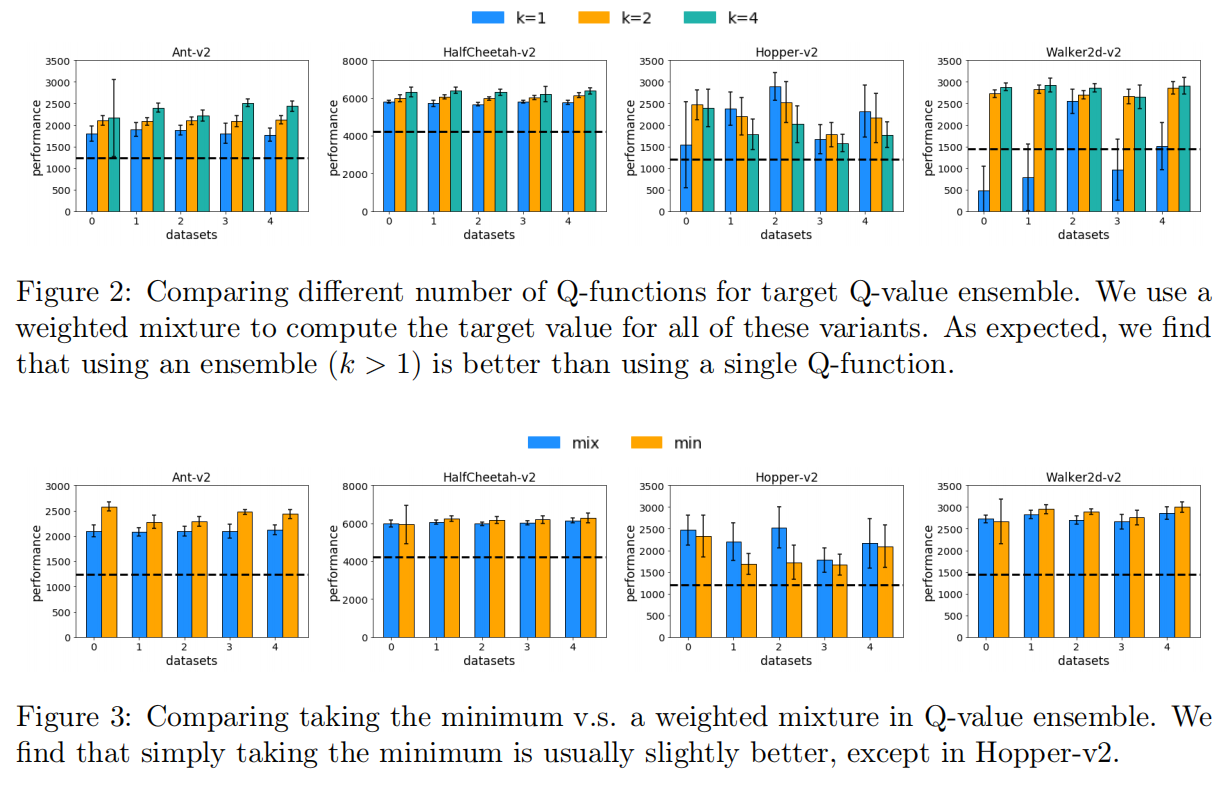
3.2 Ensemble for target Q-values

发现：BEAR和BCQ都使用多个学习 $Q$ 函数的最小值和最大值的加权混合(而TD3只使用最小的两个值),且BEAR进一步将 $Q$ 函数的数量从2增加到4。
结论：
(1) $k=1$ 或者 $k=2$ 的效果一般，只有 $k=2$ 和 $k=4$ 都显着改善了部分训练的策略基线。 一般来说，增加 ensemble 中的 $k$ 值会导致更稳定或更好的性能，但需要更多的计算成本。 但发现 $k=4$ 仅比 $k=2$ 提供marginal improvement，因此后文实验用了 $k=2$
(2) 除了Hopper之外，取混合值比取最小值略好外，其他所有情况取最小值均比混合值好。由于取最小两个Q函数的简单性和强性能，后续的实验中使用了这种方法。(如图3)

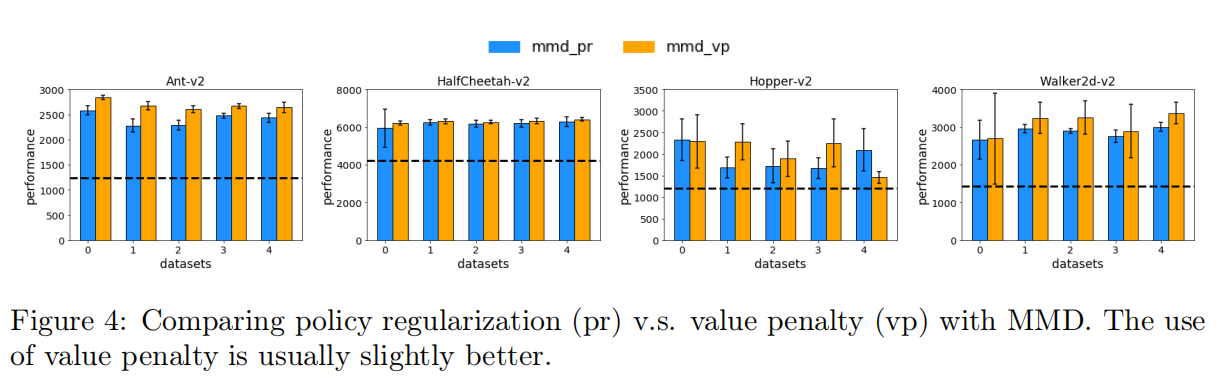
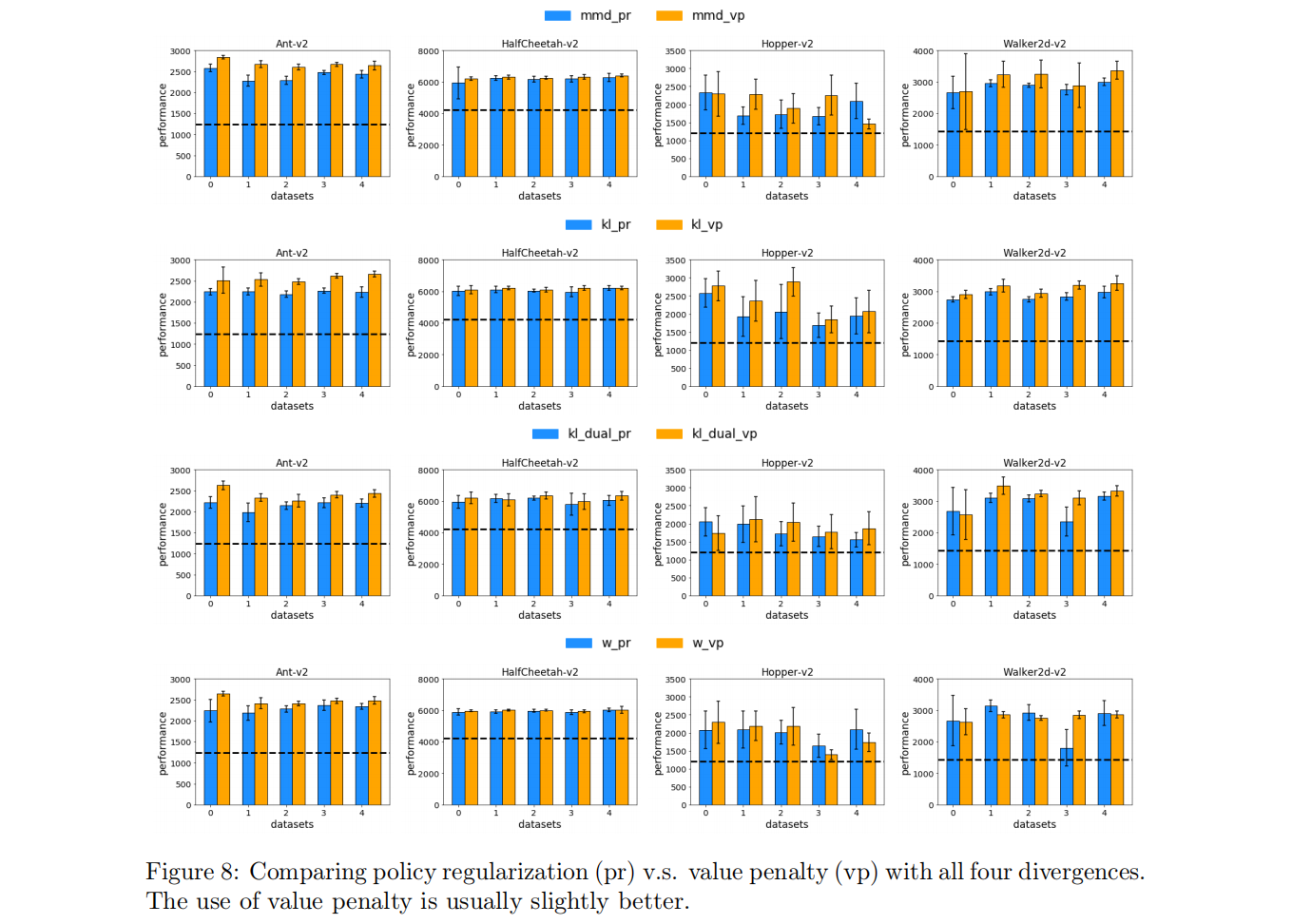
3.3 值函数惩罚或策略正则化

实验基础

• MMD policy regularization
• fixed $\alpha$,
• computation of target Q-values based on the minimum of a $k=2$ ensemble
  

发现：在4种环境中，虽然这VP和PR都优于部分训练的策略，但发现VP 价值惩罚在大多数情况下的性能略优于PR 策略正则化。我们在其他差异选择中一致地观察到这种优势（完整的比较见附录图8）。

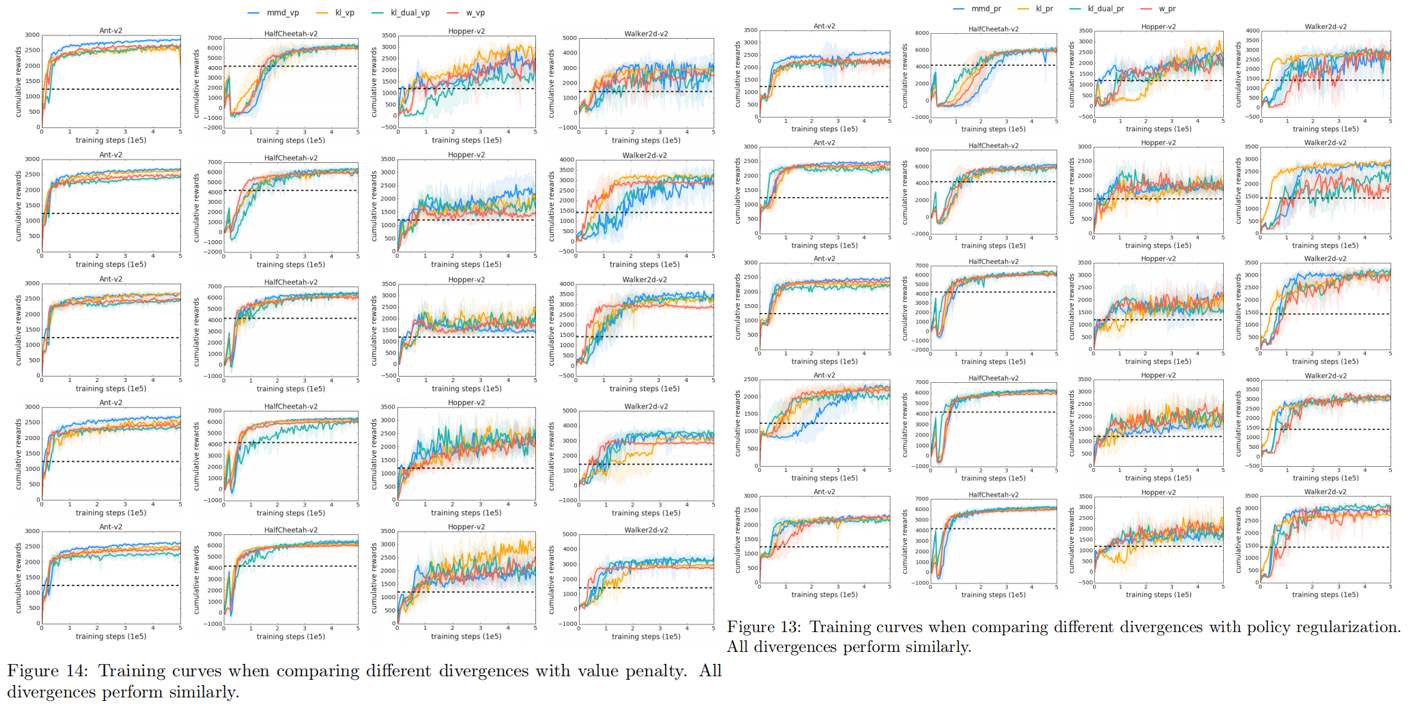
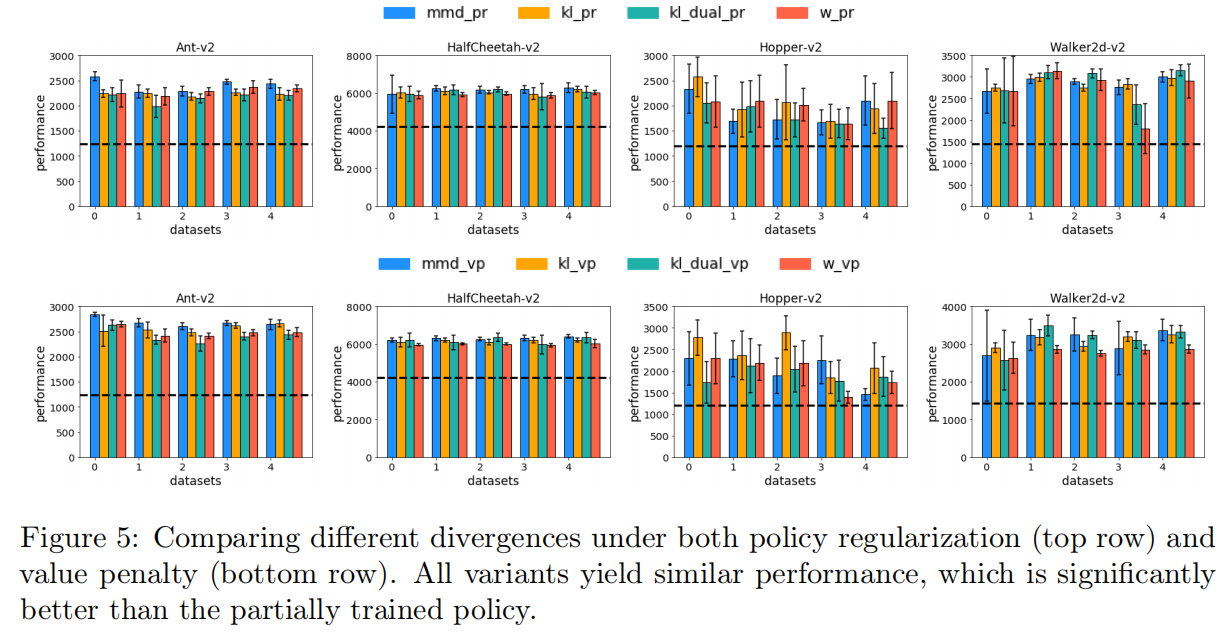
3.4 正则化之间的差异

发现与结论： Kumar认为在BEAR中 kernel MMD优于KL，因为将学习策略分布的支持应该在行为策略的支持范围内，而不是强迫两种分布相似,虽然在概念上是合理的，但作者在实验中没有找到支持这一论点的证据，另外整体来说PR和VP中误差范围并不大，但在hopper环境中除外，其他的来说MMD、KL、f-divergence和WD的差别并不大。

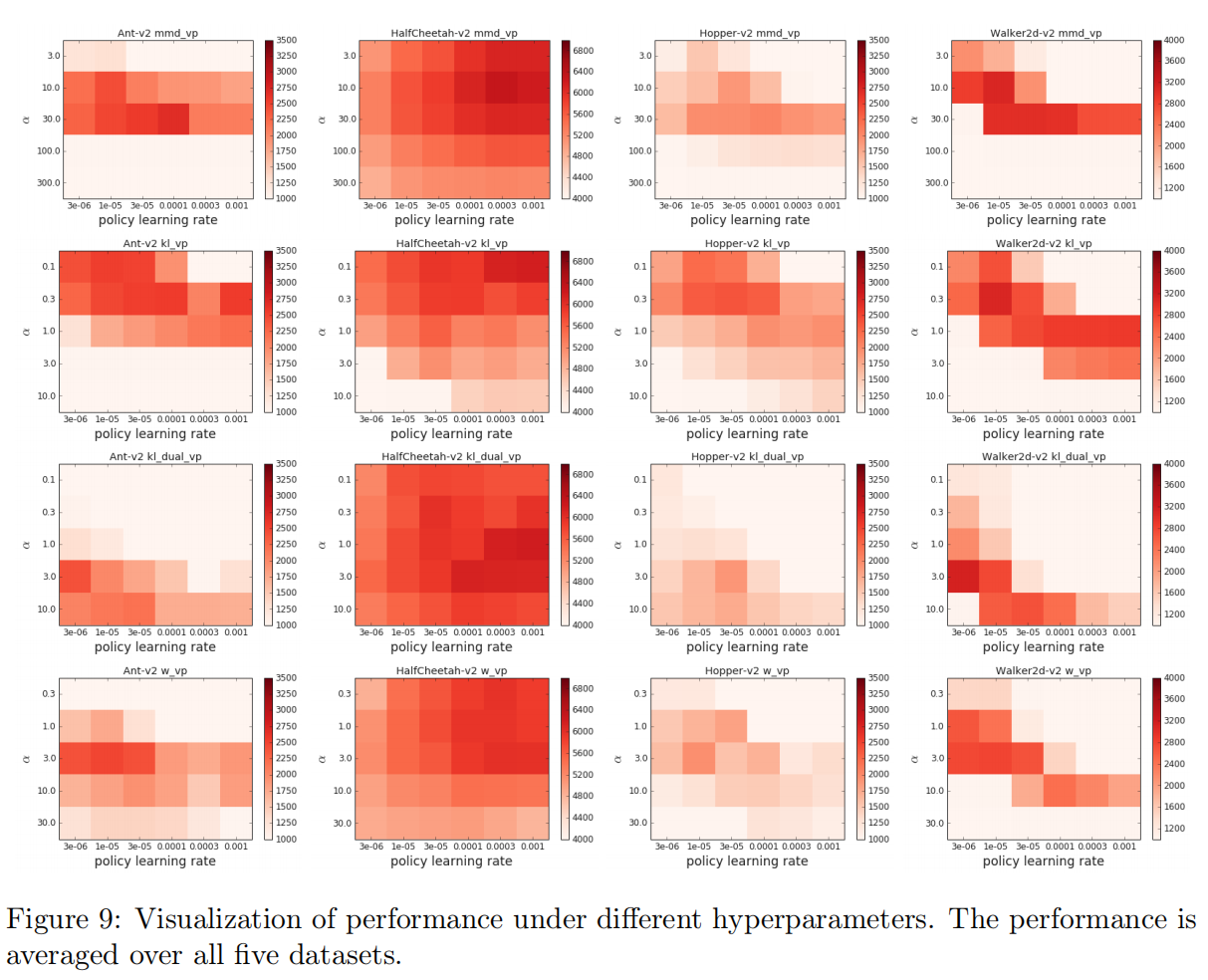
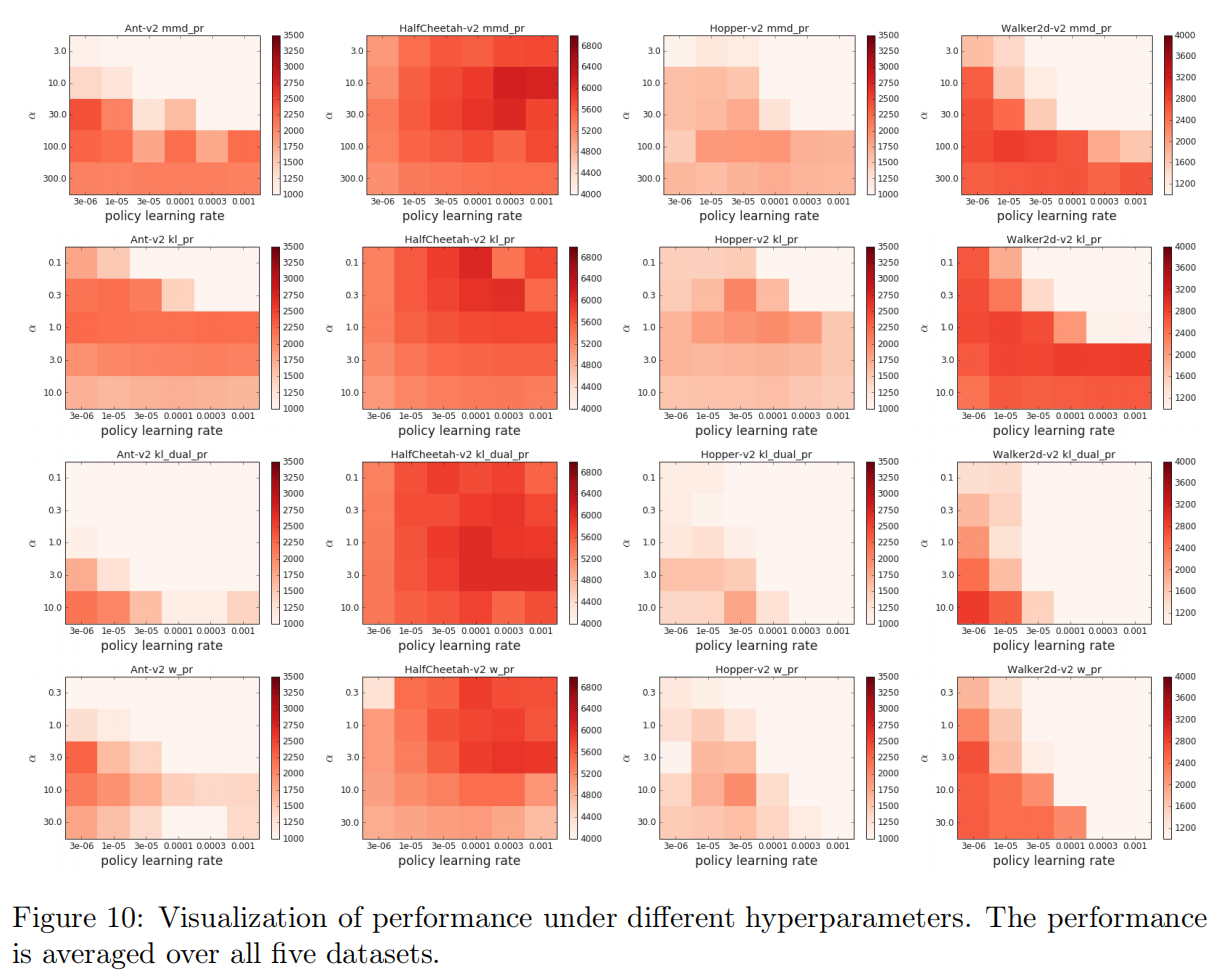
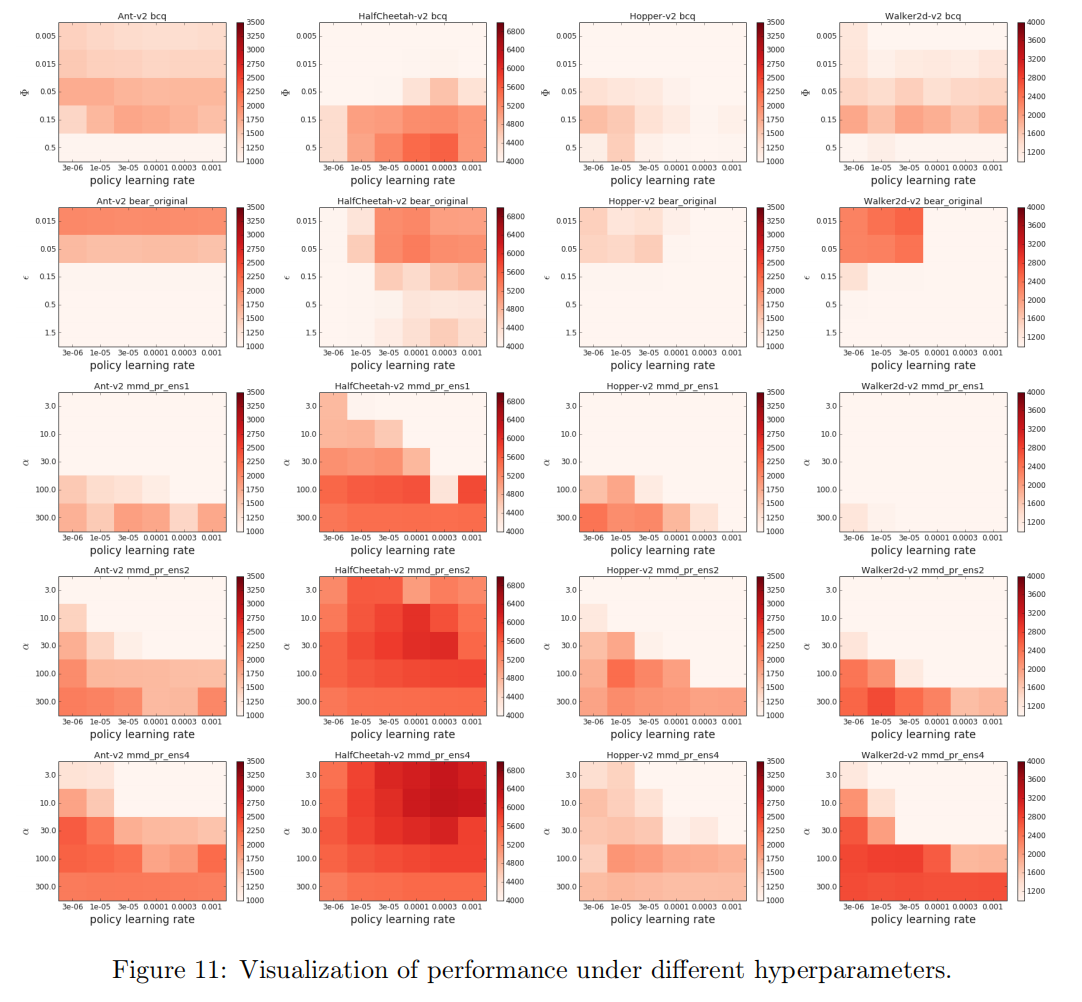
3.5 超参数敏感性(Hyperparameter Sensitivity)

这一块是整个实验的重点部分，首先放出实验的关键参数，比如BCQ中 $\Phi$ , BEAR 中的 $\epsilon$ , 以及MMD中的 $\alpha$ 等参数。

3.6 BCQ和其他Baseline的比较

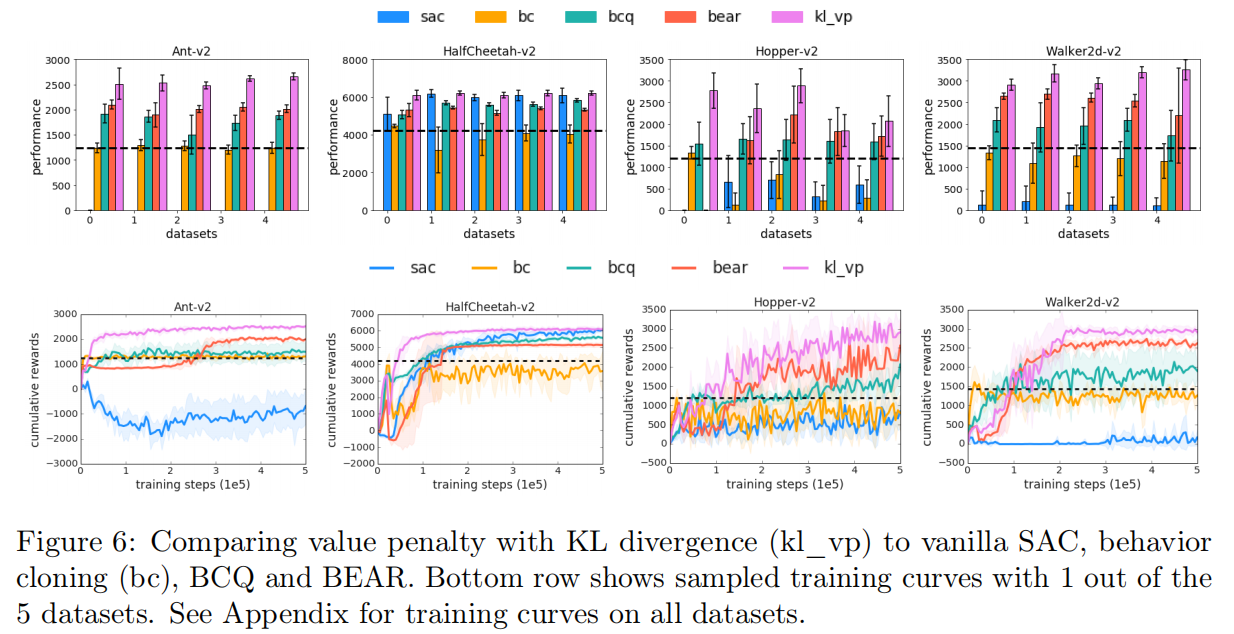
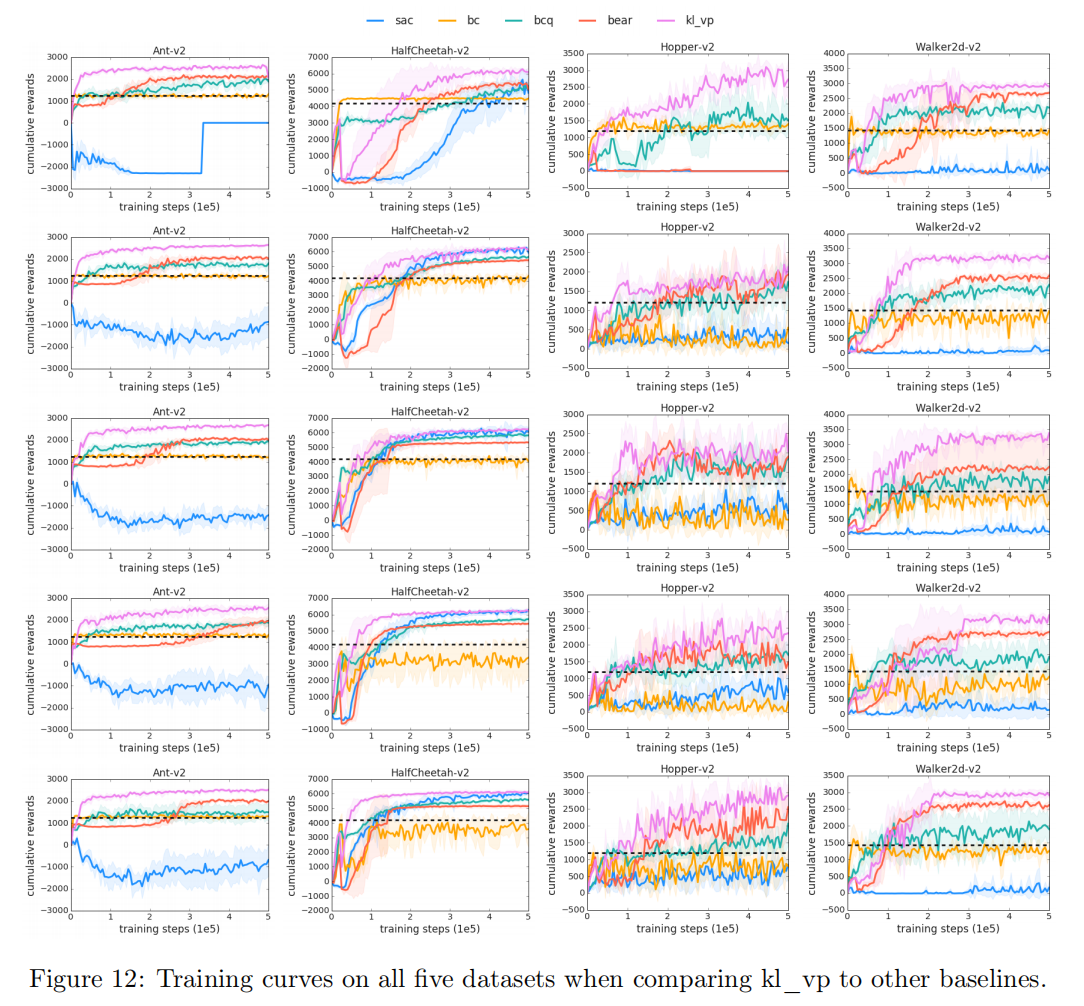
结论： 作者比较了迄今为止性能最好的算法之一，kl_vp(原始形式的KL散度的值惩罚)、BCQ、BEAR和其他两个基线：vanilla SAC（使用自适应熵正则化）和行为克隆。图6显示了比较。结果表明
（1） vanilla SAC只在HalfCheetah环境中工作，而在其他三种环境中失败。
（2） 行为克隆从来没有学习到比用于收集数据的部分训练的策略更好的策略，尽管BCQ始终学习比部分训练策略更好的策略，但它的性能总是明显比kl_vp差。
结论： BCQ不如明确使用行为正则化(BEAR和kl_vp)好用。

3.7 模型训练超参数汇总

4. 代码

【Code】Behavior Regularized Actor Critic

5. 拓展阅读

[1]. Haoran Xu, Xianyuan Zhan, Jianxiong Li, Honglei Yin: “Offline Reinforcement Learning with Soft Behavior Regularization”, 2021; arXiv:2110.07395.
[2]. Chi Zhang, Sanmukh Rao Kuppannagari, Viktor K Prasanna: “BRAC+: Improved Behavior Regularized Actor Critic for Offline Reinforcement Learning”, 2021; arXiv:2110.00894.

参考文献

[1]. Yifan Wu, George Tucker, Ofir Nachum: “Behavior Regularized Offline Reinforcement Learning”, 2019; arXiv:1911.11361

OfflineRL推荐阅读

离线强化学习(Offline RL)系列3: (算法篇)策略约束 – BEAR算法原理详解与实现
离线强化学习(Offline RL)系列3: (算法篇)策略约束-BCQ算法详解与实现
离线强化学习(Offline RL)系列2: (环境篇)D4RL数据集简介、安装及错误解决
离线强化学习(Offline RL)系列1：离线强化学习原理入门

今天的文章离线强化学习(Offline RL)系列3: (算法篇)策略约束 – BRAC算法原理详解与实现(经验篇)分享到此就结束了，感谢您的阅读。