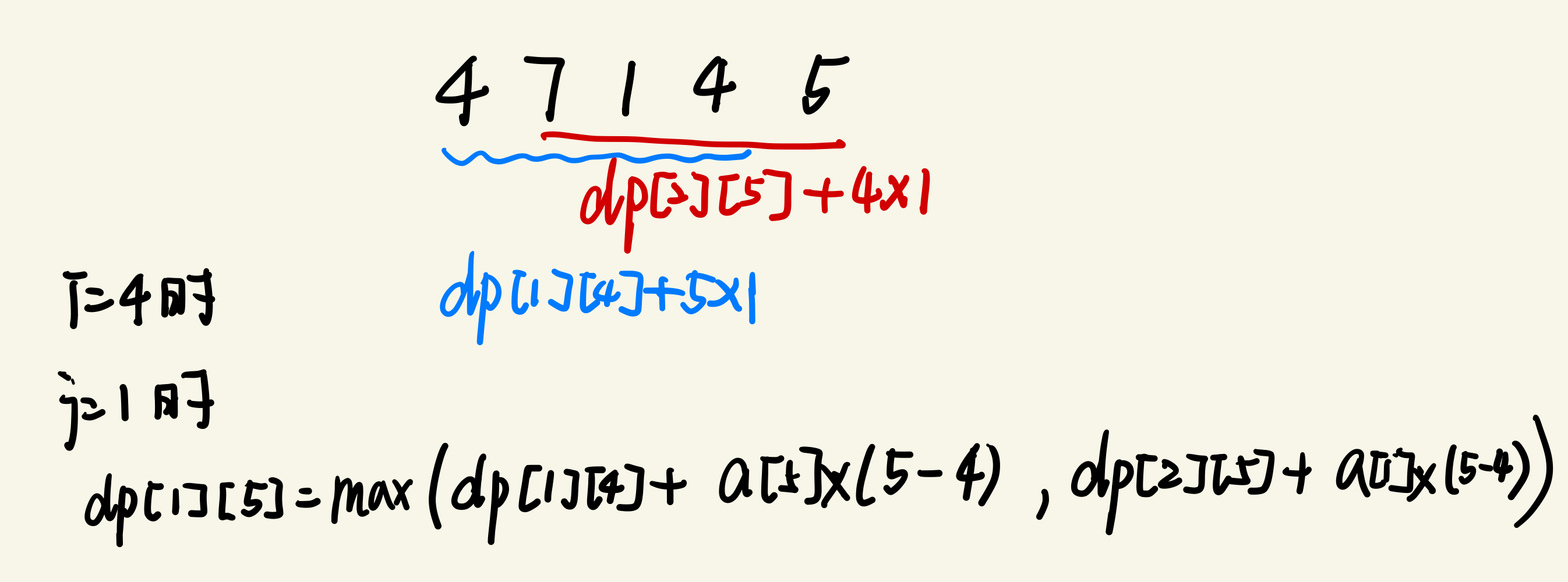acwing动态规划_acm经典例题

ACM题解——动态规划专题——奶牛食物的最大收益

题目描述

FJ has purchased N (1 <= N <= 2000) yummy treats for the cows who get money for giving vast amounts of milk. FJ sells one treat per day and wants to maximize the money he receives over a given period time.

The treats are interesting for many reasons:

• The treats are numbered 1..N and stored sequentially in single file in a long box that is open at both ends. On any day, FJ can retrieve one treat from either end of his stash of treats.
• Like fine wines and delicious cheeses, the treats improve with age and command greater prices.
• The treats are not uniform: some are better and have higher intrinsic value. Treat i has value v(i) (1 <= v(i) <= 1000).
• Cows pay more for treats that have aged longer: a cow will pay v(i)*a for a treat of age a.

Given the values v(i) of each of the treats lined up in order of the index i in their box, what is the greatest value FJ can receive for them if he orders their sale optimally?

The first treat is sold on day 1 and has age a=1. Each subsequent day increases the age by 1.

 

Input

Line 1: A single integer, N

Lines 2..N+1: Line i+1 contains the value of treat v(i)

 

Output

Line 1: The maximum revenue FJ can achieve by selling the treats

 

Sample Input

5
1
3
1
5
2

Sample Output

43

 

Hint

Explanation of the sample:

Five treats. On the first day FJ can sell either treat #1 (value 1) or treat #5 (value 2).

FJ sells the treats (values 1, 3, 1, 5, 2) in the following order of indices: 1, 5, 2, 3, 4, making 1×1 + 2×2 + 3×3 + 4×1 + 5×5 = 43.

题意

给一串序列，有n个数，你可以从序列头或者尾取数字，取的时候需要编号，第一个数，第二个数……直至取完，最终要求出如何取数字，才能使所有取出的数字与对应编码的乘积的和最大。开始我以为取得时候可以贪心，总是先取最小的，最大的就可以拖着最后取，但是实际上并不是这样的，例如 47145这个序列，看着4<5, 取4,；然后5<7,取5；3<7,取3；1<7，取1。从先到后依次为第1 5 4 3 2个取，得出的结果为 4*1+7*5+1*4+4*3+5*2=65，可是发现那个1有点太小了，想要把它先取了试一试，就按照 4 5 3 2 1 的顺序来取数字，得出结果为4*4+7*5+1*3+4*2+5*1=67 发现比上一次的结果要更大，可见左右贪心取当前最小值并行不通。

上面的方法是从外往内剥，换一个思路从内往外、从左往右推。用dp[i][j]记录序列从j开始，长度为i+1的序列的不管用某种方法得到的最大的乘积和。对于每一个序列，已知其最大乘积和，它是由比其序列长度少一得到的，只有两种情况，要么加左边，要么加右边，加的和=max(该数字*（n-已有个数）)（ps:已有个数就是当前序列长度-1，括号里得到的就是序号<从减掉第一个算1开始,当还剩i+1个数时，是把它从剩i变成剩i+1个得到，这i+1的序号就为n-i>），两层循环依次类推求出最后的dp[1][n]就是最终的答案。

因此可以得到状态方程：

做一个图示过程：

代码

#include<iostream>
using namespace std;
int maxx(int x,int y)
{
    if(x>y)
        return x;
    else
        return y;
}
int main()
{
    int n=0;
    cin>>n;
    int *v=new int [n+1];
    v[0]=0;
    for(int i=1;i<=n;i++)
        cin>>v[i];
    int **dp=new int*[n+1];
    for(int i=0;i<=n;i++)
    {
        dp[i]=new int[n+1];
        for(int j=0;j<=n;j++)
            dp[i][j]=0;
        dp[i][i]=v[i]*n;
    }
    int big=0;
    for(int i=1;i<n;i++)       //长度从1-n变化
    {
        for(int j=1;j<=n-i;j++)//左边界变化范围
        {
            int yj=j+i;        //长度为i+1，末尾为j+i=yj
            dp[j][yj]=maxx(dp[j+1][yj]+v[j]*(n-i),dp[j][yj-1]+v[yj]*(n-i));//短的补左边和短的补右边取最大值
        }
    }
    cout<<dp[1][n-1]<<endl;
    return 0;
}

今天的文章acwing动态规划_acm经典例题分享到此就结束了，感谢您的阅读。