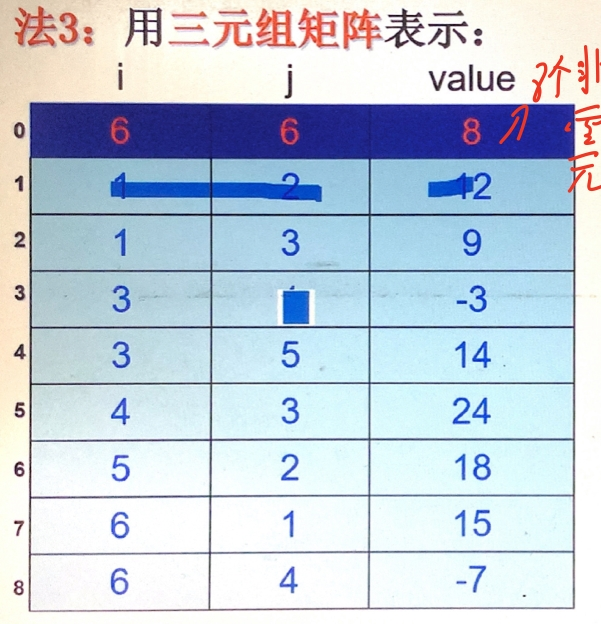
稀疏矩阵
三元组顺序表用于储存压缩后的稀疏矩阵
- 顺序存储表示
#define MAXSIZE 125000//设置非零元素的最大个数为125000
typedef struct{
int i;//元素行号
int j;//元素列号
Element e;//元素值
}Tripe;
typedef struct {
Tripe data[MAXSIZE+1];
int mu;//总行数
int nu;//总列数
int tu;//非零元个数
}TsMatrix;
三元组表的顺序存储结构
typedef struct {
Tripe data[Maxsize+1];
int nu;//矩阵总列数
int mu;//矩阵总行数
int tu;//矩阵中非零元素的个数
}TSMatrix
typedef struct{
int i;
int j;
Elementtype e;
}Tripe;
带辅助向量的三元组
主要用途
- 便于高效访问稀疏矩阵中任一非零元素
| i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| NUM(i) | ||||||
| POS(i) |
- 其中NUM用于存储每列非零元的个数
- POS用来记录每列第一个非零元素在新三元组中的位置
pos(1)=1
pos(i)=pos(i-1)+NUM(i-1)
//稀疏矩阵的转置
算法思路:
1.将每个三元组中i和j互相调换,再排序,但排序的时间复杂度
至少为o(tu^2)
2.依次从小到大找到最小的i,再转置
3.利用三元组的辅助向量精确放置转置后的元素
辅助元素的求解
NUM[i]表示第i列中的非零元素的个数
POS[i]表示第i列第一非零元素在新的三元组中行数
//求解过程如下
POS[1]=1;
for(int i=1;i<=M.tu;i++)
num[M.data[i].j]++;//求解列的NUM值
for(int i=2;i<=M.nu;i++)
POS[i]=POS[i-1]+NUM[i-1];//求解POS的值
全部算法展示
int FastTransposeSMatrx(TSMatirx M,TSMatirx *T)
{
int col;
int *NUM,*POS;
NUM=(int *)malloc((M.nu+1)*sizeof(int));
POS=(int *)malloc((M.nu+1)*sizeof(int));//动态数组
T.mu=M.nu;T.nu=M.mu;T.tu=M.tu;
if(T.tu)
{
for(col=1;col<=M.nu;col++)NUM[col]=0;
for(int i=1;i<=M.tu;i++)NUM[M.data[i].j]++;
}//这里实际是在判断了T.tu非空
POS[1]=1;
for(int i=2;i<=M.nu;i++)
POS[i]=POS[i-1]+NUM[i-1];
for(int p=1;p<=M.tu;P++)
{
col=M.data[p].j;
q=POS[col];
T.data[q].i=M.data[p].j;
T.data[q].j=M.data[p].i;
T.data[q].e=M.data[p].e
POS[col]++;
}
return 0;
}
矩阵的相乘
矩阵相乘的经典算法
for(i = 0;i < rows_a;i++)
for(j=0;j<col_b;j++)
{
sum=0;
for(k = 0;k < col_a;k++)
sum+=(a[i][k]*b[k][j]);
d[i][j]=sum;
}
//时间复杂度O(rows_a*cols_b*col__a)
稀疏矩阵相乘的高效方法
- 思路如下
设有两个矩阵A,B相乘,C为相乘后的矩阵,由于aij和bjk相乘的积是需要累加到C矩阵中的cik中的,所以对于每一行的C元素的计算,只需要从A矩阵的每一行开始,每一个非零元aij去与B中第j行的非零元相乘再累加到对应的cik中去就可以了
- 代码实现如下
#define MAXMN 500
typedef struct{
Triple data[MAXSIZE + 1];//矩阵元素
int rpos[MAXMN + 1];//各行第一个非零元素的位置表
int mu,nu,tu;//总行数,总列数,非零元素个数
}RLSMatrix;//行逻辑链接顺序表类型
int MultSMatrix(RLSMatrix M,RLSMatrix N,RLSMatrix *Q)
{
if(M.nu != N.mu) {
printf("error!");
return -1 ;
}
Q.mu = M.mu; Q.nu = N.nu;Q.tu = 0;
if(M.tu*N.tu != 0){
//若为0矩阵则没必要进行计算了
for(arow = 1;arow <= M.mu ; arow ++)
{
int count_arry[M.mu + 1] ={
0};//各元素累加器定义并清零
Q.rpos[arrow] = Q.tu + 1;//计算新矩阵的非零元素 的位置表
if(arrow < M.tu )
{
tp = M.rpos[arow + 1];
}
else tp = M.tu + 1;
//利用辅助元素记录稀疏矩阵每行首个非零元素的位
//置,在运用时需要特别注意最后一个量,他不能直
//接由后一个值来推出该行的总非零元素,而应该通
//过M.tu来获取信息
for (p = M.rpos[arrow];p < tp;p++ ) {
brow = M.data[p].j;
if (brow < N.mu) t = N.rpos[brow + 1];
else {
t = N.tu + 1;//这里是处理N矩阵在最后一个辅助元素的情况
}
for (q = N.rpos[brow]; q < t; q++){
ccol = N.data[q].j;
count_arry[ccol] +=M.data[p].e*N.data[q].e;
}//q
}//p
for(ccol = 1; ccol<=Q.nu;ccol++)
{
if(++Q.tu > MAXSIZE)return -1;
Q.data[Q.tu] = {
arow,ccol,count_arry[ccol]}
}//for
}//arow for
}//if
return 0;
}
今天的文章稀疏矩阵乘法_稀疏矩阵的快速转置题目分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/67012.html