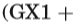thank you中文翻译_thank you中文翻译

6. EXPERIMENTS

我们可以利用传播冗余的推理来消除传播冗余。然后我们得到一个传播强度完全相同但传播器更少的模型。这可以转化为更快的传播。我们对第4节中问题去除传播冗余约束的改进进行了实证验证，除n-Queens问题外，由于n-Queens问题存在较好的单一模型，使用全局alldifferent约束，使得冗余建模不值得。

在以下实验中，所有基准测试都是在运行Solaris 8的Sun Ultra 5/400工作站上使用ILOG Solver 4.4执行的。每个表的第一列表示问题实例。 第二列描述了比较下的模型。 第三列表示搜索变量的选择。 在组合模型的情况下，我们可以选择只搜索一个模型的变量，或者从两个模型一起搜索变量。 但是，本文不讨论选择提供最小搜索空间的“最佳”搜索变量集的问题。为了比较不同模型的性能，我们测量失败的总数（第四列），以千字节为单位的总内存（第五列）和以秒为单位的CPU时间（第六列）。 标有“ – ”的表条目表示在执行一小时后无法解决问题。 为了突出消除传播冗余约束的好处，我们将完整组合模型和优化组合模型的数字放在由符号“/”分隔的同一单元格上。 为了提高组合模型的效率，我们使用ILOG Solver中的IlcInverse全局约束来实现排列通道。但是，ILOG Solver没有为其他两个通道提供这样的全局约束实现。 因此，我们已经为布尔通道实现了我们自己的全局约束，并设置了通道以使结果更加一致。

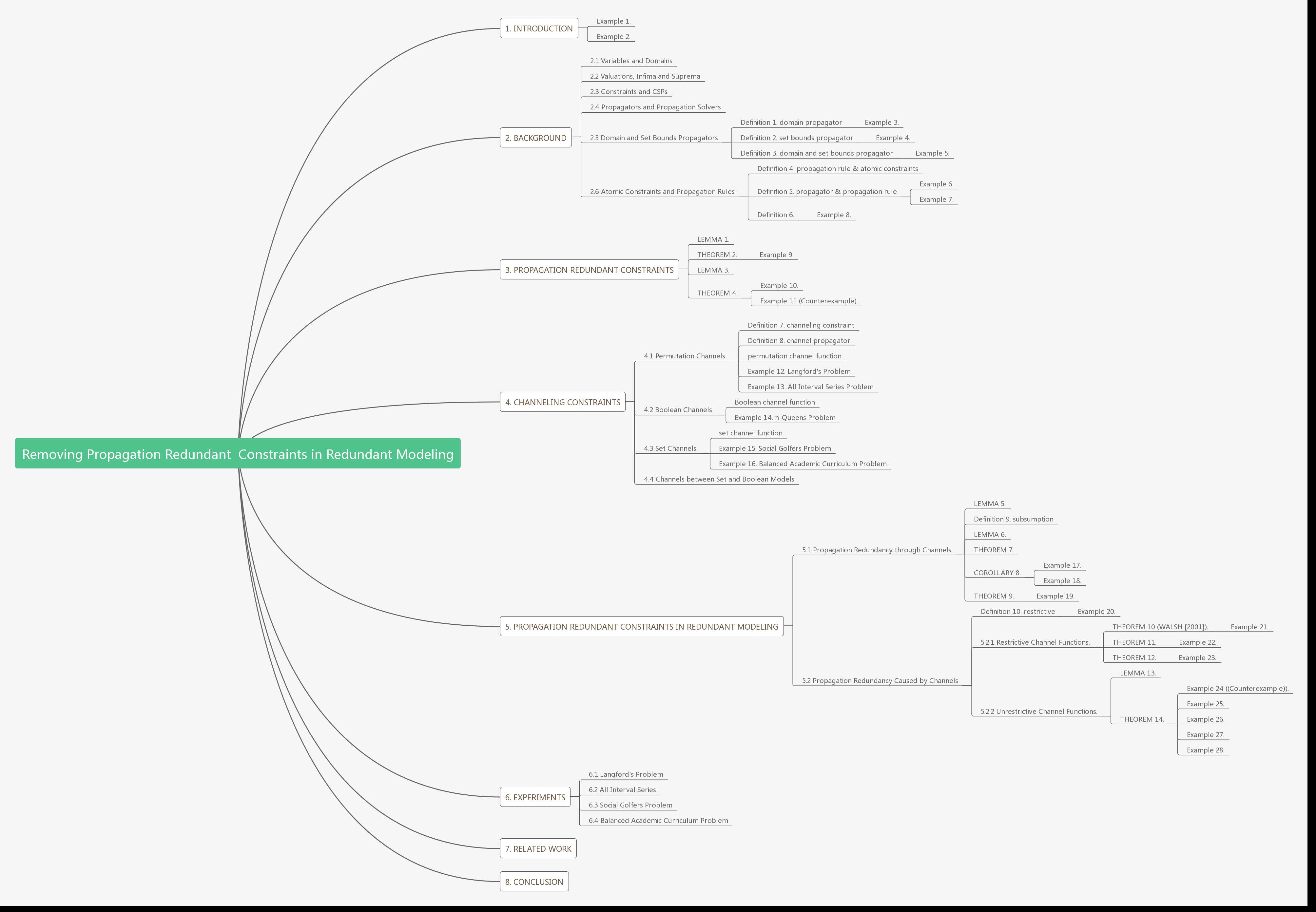
6.1 Langford’s Problem

表II比较了找到Langford问题的第一个解的不同模型。 比较的模型包括单个模型：和，完整组合模型，以及实例17和21中讨论的优化组合模型。 首先使用最小域（即ILOG Solver中的IlcChooseMinSizeInt）变量排序域中的启发式和顺序值从最小到最大。

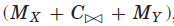
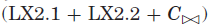
我们的opt模型对应于Smith [2000]的最小组合模型。 史密斯凭经验证明，使用最小组合模型和搜索变量X∪Y可以更有效地解决这个问题。 我们的结果与Smith提出的结果一致，其中opt模型更快并且保持与所有三组搜索变量的完整模型相同的失败次数，且具有搜索变量X∪Y的opt模型在所有被比较的模型中是最快的。除了失败的次数和时间之外，解决问题所需的内存消耗量也是衡量性能的重要指标（史密斯没有提供）。 传播冗余约束的存在消耗了许多不必要的存储空间。 从表II中，我们可以看到opt模型比相应的完整模型需要更少的内存。

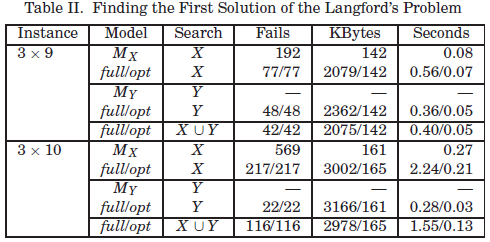
当我们解决Langford问题的所有解决方案时，消除传播冗余约束的好处更加明显（见表III）。 问题实例“4×14”和“4×15”是不可行的并且没有解决方案。 对于所有实例，实验确认opt模型与完整模型具有相同的搜索空间。 随着问题规模的增加，opt模型可以比整个模型更节省时间和内存消耗。

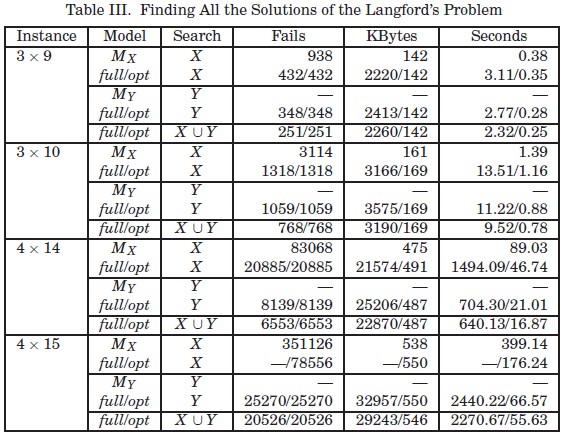
6.2 All Interval Series

找到All Interval Series问题的第一个解决方案是一个简单的问题。 挑战在于找到所有解决方案。 表IV比较了找到所有区间序列问题的所有解的不同模型。 比较的模型包括单个模型：和，完整组合模型和优化组合模型，如实施例19和21中所讨论的。我们使用最小域第一变量排序启发式和从最小到最大的域中的顺序值。

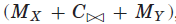
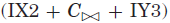
给定相同的搜索变量集（X或Y），与单个模型（和）相比，完整模型显着减少了失败次数。 但是，冗余建模的开销超过了搜索空间减少的收益。 通过从组合模型中移除传播冗余约束，具有搜索变量Y的opt模型是最快的。 该实验确认opt模型与所有测试用例的完整模型保持相同的失败次数。随着问题规模的增加，opt模型的好处对于时间和内存消耗都更加明显，并且它是唯一可以在时间限制内解决实例n = 15的模型。 opt模型的内存消耗量与单个型号（，）相比具有竞争力，而不是整个模型的巨大内存开销。

6.3 Social Golfers Problem

社交高尔夫球手问题具有大量对称解决方案，搜索所有解决方案是不切实际的。 表五比较了发现社交高尔夫球手问题的第一个解决方案的不同模型。 在实施例15中描述了使用参数g-s指示的问题实例。 比较的模型包括单个模型：和，完整组合模型，以及优化的组合模型，如实施例23和27中所讨论的。以下启发式用于变量排序。 对于搜索变量X，我们使用变量的升序索引，变量是按周排序的玩家。 Barnier和Brisset [2002]表明，这种启发式方法可以有效地解决8-4-9个实例。 对于搜索变量S和X∪S，我们只使用最小域第一个从最小到最大排序的值。

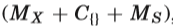
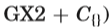
实验验证了opt模型与完整模型具有相同的失败次数，同时加快了搜索速度，降低了所有测试用例的内存消耗。与单个模型MS相比，带有搜索变量S的组合模型(full和opt)减少了失败的次数，但与带有搜索变量x的MX相比，情况并非如此。在例4-3-4，带有搜索变量S的opt模型是最快的；在例7-2-13，带有搜索变量X∪S的opt模型是最快的；在例例如8-4-9和9-2-17，单独一个模型MX是最快的。

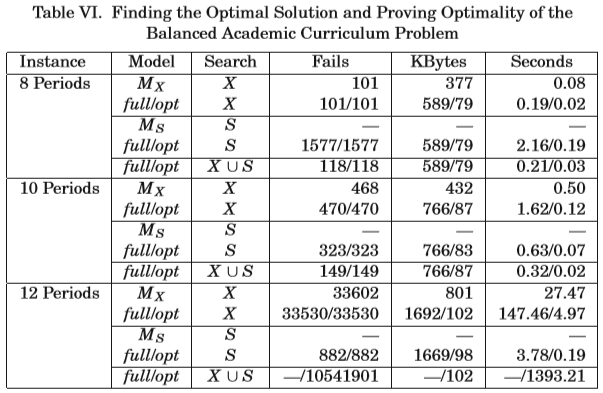
6.4 Balanced Academic Curriculum Problem 

Hnich等[2002]报道，仅用基于传播的约束求解器找到平衡学术课程问题的最优解是困难的。 这个问题的挑战是找到最优解并证明最优性。 表VI比较了发现CSPLib中平衡学术课程问题的三个问题实例的最佳解决方案和证明最优性的不同模型。比较的模型包括单一模型和、完整的组合模型以及优化的组合模型，如示例18、23和28所述。下面的启发式用于变量排序。我们对搜索变量X和X∪S使用最小域，并且对搜索变量S使用变量索引的升序。值从最小到最大排序。

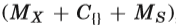
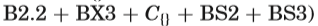
值得注意的是，在添加了冗余约束(B2.1)和(B2.2)之后，我们能够单独使用MX解决所有的问题实例。实验证明，对于三组搜索变量，opt模型的失败次数与完整模型相同。opt模型比完整模型更快，消耗的内存更少。值得注意的是，对于这个问题，opt模型的内存消耗是最小的，甚至小于单个模型MX。opt模型的性能明显优于其他模型。对于具有8个周期的实例来说，具有搜索变量X的opt模型是最快的；在具有10个周期的实例里，具有搜索变量X∪S的opt模型是最快的，并且具有最少的失败数量；在具有12个周期的实例里，具有搜索变量S的opt模型是最快的，且失败次数最少。

7. RELATED WORK

Smith [2000,2001]研究了许多个体问题的冗余模型，包括n-Queens问题，Langford问题和社交高尔夫球手问题。 史密斯凭经验证明，可以在不增加搜索空间的情况下去除冗余模型中的一些约束。 史密斯指出，对于这些问题，所谓的最小组合模型，其使用信道约束将第一模型和仅第二模型的变量（没有约束）组合，产生与完全组合模型相同的搜索行为。 Choi和Lee [2002]以临时方式证明了这一点。 在本文中，我们的目标是一个理论框架，它可以先验地确定冗余模型中涉及的特定约束的传播冗余。

Apt和Monfroy[2001]开发了“成员规则”作为构建任何约束的传播器的方法。当限制为整数变量时，传播规则类似于“成员规则”。但是，我们开发了传播规则作为对传播器行为的各个部分进行推理的方法。

Brand[2003]在基于规则的约束编程中给出了一个确定规则相对于一组规则传播冗余的一般定理，并使用“成员规则”说明了其适用性。事实上，我们对传播规则的定义满足布兰德定理所要求的性质。因此，我们可以应用Brand定理来确定传播规则相对于一组传播规则何时是冗余的。在本文中，我们感兴趣的是超越单个传播规则的传播冗余，而是约束作为一个整体的传播冗余。我们还通过信道函数推广了传播规则的传播冗余的概念。

Hnich等[2004]和Walsh[2001]引入约束紧密度的概念作为比较不同排列约束的传播强度的度量。他们的工作重点是，仅在排列问题和注入问题的冗余建模中，比较在不等式, 通道约束，和所有不同的全局约束的不同的一致性概念的传播强度。我们的比较测度类似于约束紧性，只是约束紧性是由局部一致性参数化的。然而，在现有的约束求解器中，存在没有实现任何(已建立的)局部一致性属性的传播器。一个例子是Apt [2003, pp. 219-220]中讨论的整数域上的乘法约束x = y×z。在约束的局部一致性未知的情况下，我们的比较方法仍然适用。在本文中，我们感兴趣的不仅是排列约束的传播，而且还有冗余模型中的其他约束。我们还讨论了排列通道之外的更广泛的通道约束。

Walsh[2003]证明了集合(多集合)变量上的“边界一致性”等价于对应出现表示上的边界一致性。这个结果与定理15有关，因为集合变量的出现表示对应于4.4节中描述的布尔变量。但是，现有约束求解器会将布尔约束分解为多个部分并分别传播每个部分。 我们基于这个更现实的假设来证明该定理。

定理4的一个推论是，我们可以仅使用单个域传播器来确定整整数CSP与树结构的域一致性，因为我们可以反复应用上面的引理将约束的并集分解为单个约束。这与Freuder的树结构求解csp的“无回溯”方法高度相关[1982]。

8. CONCLUSION

本文的贡献有三个方面。 首先，我们根据通道函数定义通道约束，这允许我们覆盖广泛形式的冗余建模。 通过将传播器分解为单独的传播规则，我们推断一个模型中的约束可以通过通道中的其他模型中的约束来使传播冗余。 其次，我们引入了限制性和非限制性通道函数的概念来表征通道约束。约束信道函数本身可以使组合模型传播中的约束冗余。非限制性信道函数允许检测一个模型中的约束相对于另一个模型中的约束的传播冗余，并仅根据逻辑结果检测信道。第三，基准测试结果证实，从组合模型中移除传播冗余约束通常可以在相同的搜索空间和更少的内存中实现更快的实现。如第7节所述，本文通过覆盖冗余模型中所有约束的传播冗余的更广泛形式的冗余建模和推理来扩展相关工作。

虽然我们主要关注域和集合边界传播器，但是我们的许多结果可以用于其他传播器。引理6可以应用于任何传播器，因为它只依赖于传播规则。我们可以使用定理7、9、14和推论8来证明c比dsb(c)弱的传播器是冗余的，或者c比dsb(c)强的传播器使另一个传播器冗余。

我们的工作为研究提供了许多重要的未来发展方向。 有趣的是，研究删除传播冗余约束的过程是否可以（半）自动化。 为了使用定理9，我们可以直接定义许多约束的传播规则（在Dinit中参数化）或使用Abdennadher和Rigotti [2002]的方法自动构造它们。 然而，大多数约束的传播规则的数量是指数的。对于更复杂的现实应用程序来说，一个简单的实现在计算上太昂贵并且不切实际。 一种可能的方法是考虑参数化传播规则，该规则表示一组传播规则，从而大大减少了规则的数量。 我们还可以尝试使用定理14来证明传播冗余，而不考虑传播规则。

由传播冗余约束引起的计算开销量取决于在约束传播期间处理约束的顺序和事件。 我们的实验平台ILOG Solver是一个专有的约束编程库，它不提供对这些信息的访问。 研究传播冗余约束从模型中消除后，这些因素如何影响约束求解的性能将是有趣的。

我们现有的方法在搜索之前静态地分析模型中冗余约束的传播行为。 有趣的是，研究一种在搜索过程中动态分析冗余约束的传播行为的替代方法。 基于动态分析的结果，约束求解器应避免（尽可能）在约束传播期间处理传播冗余约束。 这将最小化传播冗余约束所引起的计算开销，即使它们存在于模型

中也是如此。

冗余建模导致需要决定在搜索期间标记哪些变量。如第6节所示，搜索变量的选择可以极大地影响搜索空间的大小。例如，Geelen [1992]， Smith [2000;和Hnich等[2004]也表明，搜索变量的某些选择确实会导致搜索空间变小。因此，研究和建立选择更好的搜索变量集的标准是很有趣的。

今天的文章thank you中文翻译_thank you中文翻译分享到此就结束了，感谢您的阅读。