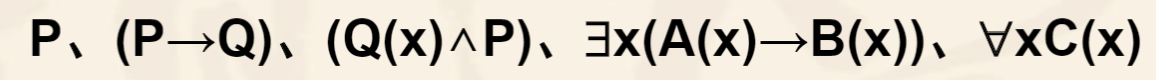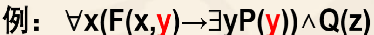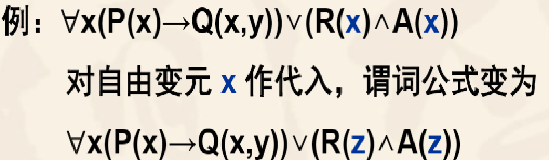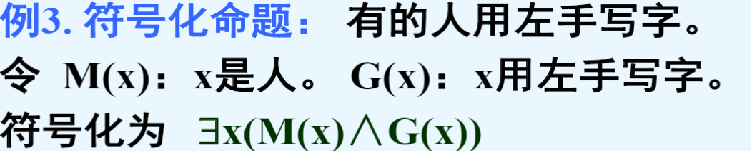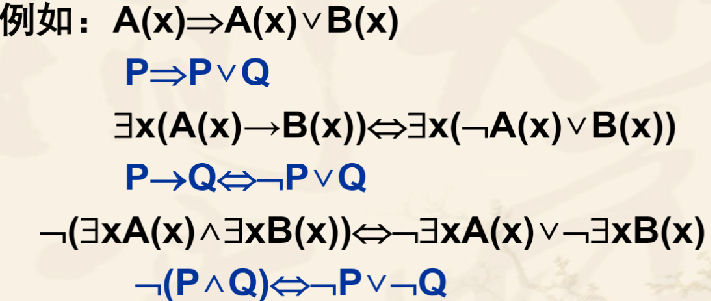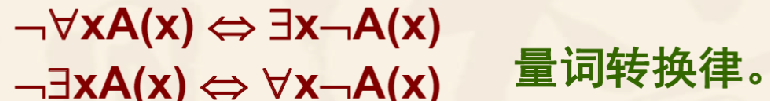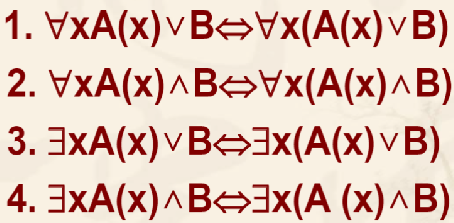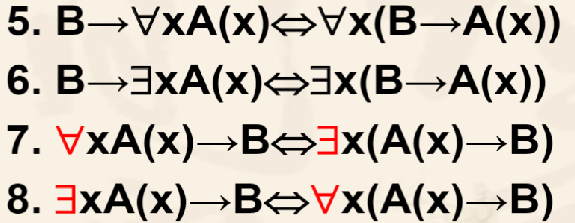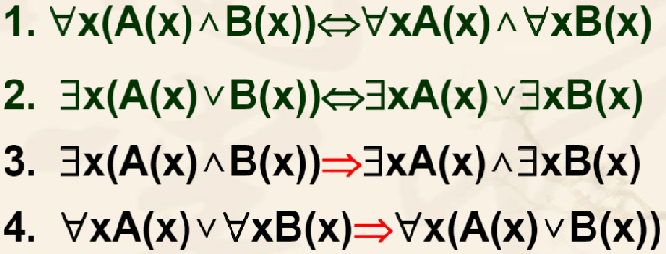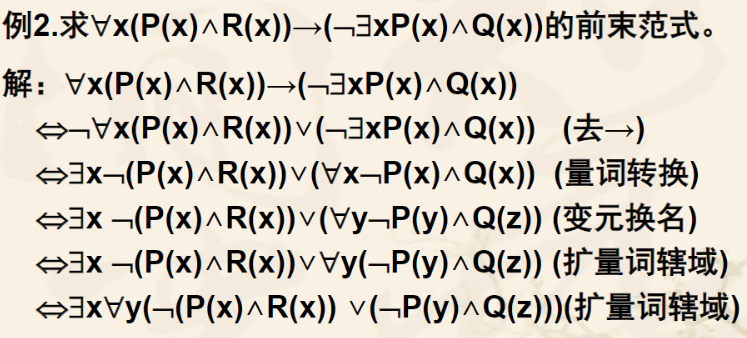离散数学谓词逻辑公式_离散数学思维导图

1.谓词逻辑基本概念

能够独立存在的具体或抽象的事物，称之为个体，也称之为客体。通常用小写英文字母a、b、c…表示
例如：小张、小李、8，a，沈阳，社会主义都是客体。
个体常项:具体的或特定的个体。常用a,b,c,…等小写字母表示
个体变元:泛指某一个个体。常用x,y,z,…等小写字母表示
谓词：用以刻化个体属性或者表达个体之间关系的词，即为谓词。谓词用大写字母表示。


谓词也有常项与变项之分。表示具体性质与关系的谓词称为谓词常项。泛指某–性质或关系的谓词称为谓词变项。

将不带个体变元的谓词称为0元谓词。例如，S(a)， G(3,7) 等。当谓词是常项时，0元谓词是命题;否则当谓词是变项时，0 元谓词是命题变元。
含有n个变元的命题函数是以个体域为定义域，以{ F,T }为值域的n元函数。

注意:命题函数本身并不是命题，只有在括号内填入足够的具体客体，或用足够的量词约束后才变成命题。

个体变元的取值范围，称之为个体域，也称之为论域。
由所有个体构成的个体域，称之为全总个体域。它是“最大的个体域。
约定:对于一个命题函数，如果没有指明其个体域，则假定其个体域是全总个体域。

2.量词

在命题中，表示对个体量化的词，称之为量词。例如:有些人是大学生。所有事物都是发展变化的。有些“所有的”就是对个体量化的词。
有两种量词

量词的指导变元:量词后边要有一个个体变元，指明对哪个个体变元进行量化，称此个体变元是指导变元。
当F是谓词常项时，∀xF(x) 是一个命题。
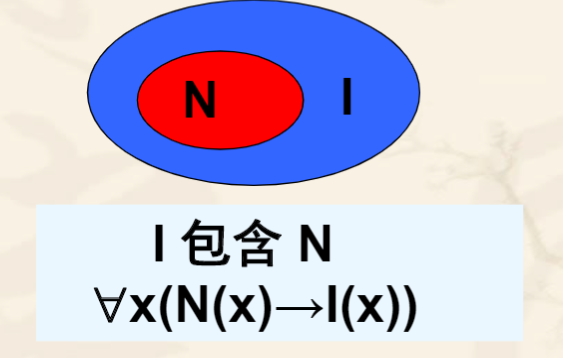
例：所有的自然数都是整数
若没设个体域，即个体域为全总个体域，则需用特性谓词加以限定。
设N(x): X是自然数(特性谓词)。l(x): x是整数。此命题可以写成∀x(N(x)→l(x))。
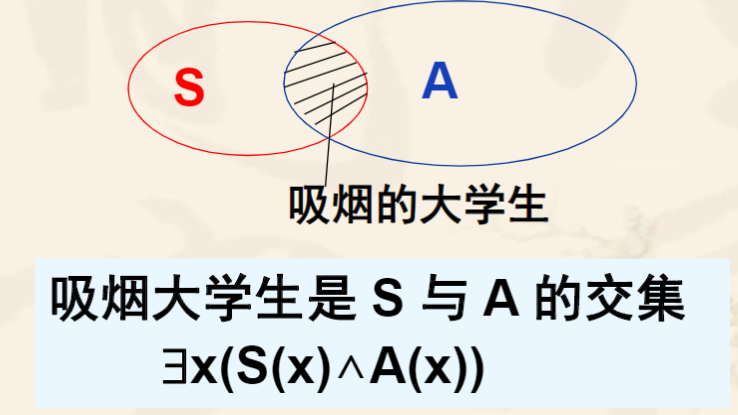
有些大学生吸烟。∃x(S(x)∧A(x))
特性谓词:一般来说，特性谓词是描述个体特征的谓词，往往就是给定命题中量词后边的那个名词。
比如:有些大学生吸烟中，有些后面的大学生是特性谓词。
特性谓词的添加规则:
对全称量词，特性谓词常作蕴涵前件。
对存在量词，特性谓词常作合取项。

分析一-下特性谓词和原谓词所表达概念之间的关系:对于全称量词:例如，所有的自然数都是整数。
令N:自然数集合，|:整数集合。

对于存在量词:例如，有些大学生吸烟。令S:大学生集合，A:烟民的集合。

每个人都有一个生母：
设P(x):x是人，M(x,y):y是x的生母
∀x(P(x)→∃y(P(y)∧M(x,y)))

谓词公式：

原子谓词公式：称n元谓词P(x1,x2,…xn)为原子命题公式
例如P,Q(x),B(x,y,a)都是原子谓词公式
谓词合式公式定义：
二、谓词合式公式
定义(1) 原子谓词公式是合式公式。
(2)如果A是合式公式，则¬A也是合式公式。
(3)如果A、B是合式公式，则(A∧B)、(A∨B)、(A→B)、(A<->B)都是合式公式。
(4)如果A是合式公式，x是A中的个体变元，则∀xA和∃xA也是合式公式。
(5)只有有限次地应用(1)至(4)得到的符号串才是合式公式。
合式公式也称为谓词公式，简称公式。
下面都是合式公式:

注意:若量词后边有括号，则此括号不能省略。例如上述公式3中量词括号不能省略。

量词的作用域

一、量词的作用域

量词的作用域(辖域)：在谓词公式中，量词的作用范围称之为量词的作用域，也叫量词的辖域。

一般地：
如果量词后边只是一个原子谓词公式时，该量词的辖域就是此原子谓词公式。例如: ∀xA(x)
如果量词后边是括号，则此括号所表示的区域就是该量词的辖域。例如: ∃x(A(x)→B(x))
如果多个量词紧挨着出现，则后边的量词及其辖域就是前边量词的辖域。
例如:∀x∃y∀z(A(x,y)→B(x,y,z))∧C(t)

自由变元与约束变元

在谓词公式中的个体变元可以分成两种，一种是受到量词约束的，一种是不受量词约束的。

定义:如果客体变元x在∀x或者∃x的辖域内，则称x在此辖域内约束出现，并称x在此辖域内是约束变元。否则x是自由出现，并称x是自由变元。

注意：(1)一个n元谓词P(x1…xn), 若在前边添加k个量词，使其中的k个个体变元变成约束变元，则此n元谓词就变成了n-k元谓词。
(2)一个谓词公式如果无自由变元，它就表示一个命题。

y既是自由变元，也是约束变元。为避免混淆，需要对约束变元换名。

换名规则

约束变元的换名规则:设A为一谓词公式，将A中某量词辖域内的一个约束变元的所有出现及相应的指导变元全部改成A中没出现过的某个变元符号，A中其余部分不变，所得公式为A’，则A⇔A’。

对自由变元也可以换名，此换名叫代入。
自由变元的代入规则:设A为一谓词公式，将A中某个自由出现的个体变元的所有出现用某个A中没出现过的变元符号代替，A中其余部分不变，记所得公式为A’，则A⇔A’。

谓词演算中的命题符号化

三种基本类型

命题的符号化表达式与个体域有关系。而个体域的指定需随题目而定。能指定个体域的当然要指定，这样会使表达式变得简。若不指定个体域，则为全总个体域。
在谓词演算中，最基本的命题符号化就三种类型:
1、主语、宾语是具体个体对象的，用谓词加括号，括号里是具体个体表示。

2、描述所有的、任意的个体对象，用全称量词，特性谓词作蕴含前件。

若写成∃x(M(x)∧F(x))则表示宇宙间的所有个体都是人并且都会呼吸

3、描述一些客体对象， 用存在量词，特性谓词作合取项。

若写成∀x(M(x)→F(x))则表达宇宙间存在某个个体，若这个个体是人，则它用左手写字

举例

不是所有的自然数都是偶数
N(x):x是自然数，E(x):x是偶数
¬(∀x(N(x)→E(x)))
不是所有的按照字面直接翻译，为¬∀x
这句话也等价于存在一些自然数不是偶数
∃x(N(x)∧¬E(x))

没有不犯错误的人
M(x):x是人，F(x):x会犯错误
¬∃x(M(x)∧¬F(x))
这句话也等价于：所有的人都会犯错误
(∀x(M(x)→F(x)))

所有大学生都喜欢一些歌星
S(x):x是大学生，G(x):x是歌星，L(x,y):x喜欢y
∀x(S(x)→∃y(G(y)∧L(x,y)))

每个自然数都有唯一的后继数

在有些命题中，某些个体对象的量词没有明确给出，要仔细分析并写出这些隐含的量词。

金子发光，但闪光的不一定都是金子
令G(x):x是金子，F(x):x闪光
命题表达为：
∀x(G(x)→F(x))∧¬∀x(F(x)→G(x))
或者
∀x(G(x)→F(x))∧¬∃x(F(x)∧¬G(x))

命题的符号表达式中所有个体变元必须都是约束变元，才表示命题。即在命题的符号表达式中，一定没有自由变元。

谓词演算的等价与蕴含

命题逻辑中命题有两个真值，可以画真值表
对谓词公式赋值(给谓词公式一个解释)
对一个谓词公式赋值由如下四部分组成:
(1)指定非空个体域集合;
(2)将谓词公式中的命题变元，用确定的命题替代;
(3)对公式中的个体变元用论域中的具体个体替代;
(4)对公式中含有的谓词变项，用谓词常项替代。

例:给公式P→N(x)作赋值。
个体域:实数集合;
P:2>1;
N(x): x是自然数; x=4.是它的一个赋值:此公式变成T→ N(4),它的真值为T

一个不含自由变元的谓词公式是命题。而含有n个自由变元的原子谓词公式，可以看成是命题变元。所以只要不牵涉到量词的运算，命题演算中的等价公式和重言蕴含公式均可推广到谓词演算中使用。

谓词公式的永真式
给定谓词公式A,如果不论对其作任何赋值，都使得谓词公式A的真值为真，则称A为永真式。
例如，公式l(x)∨¬l(x)
谓词公式的等价公式:给定谓词公式A、B，如果A<->B是永真式，则称A与B等价，记作A⇔B.
等价于说，如果不论对A、B作任何同样的赋值,A与B的真值都相等，则A与B等价。例如，N(x)→l(x)⇔N(x)∨l(x)。

给定谓词公式A、B,如果A→B为永真式，则称A永真蕴含B，记作A=>B。

有限个体域下的量词消去公式

有限个体域消去量词的等价公式，设论域为{a1,a2…an},.则

1. ∀xA(x)⇔A(a1)∧A(a2)∧A(a3)…∧A(an)
2. ∃xA(x)⇔B(a1)∨B(a2)∨B(a3)…∨B(an)
   谓词逻辑与命题逻辑的区别在于命题的表达不同。谓词公式与命题公式的最大区别在于多了量词,
   
   

量词转换率

谓词逻辑与命题逻辑的区别在于命题的表达不同。谓词公式与命题公式的最大区别在于多了量词，而所有的命题表达式都可以表示成只含有联结词∧∨¬的表达式，所以只要研究清楚量词与∧∨¬之间的关系，谓词表达式的运算也就清楚
一、量词否定等价公式（量词与¬的关系）

直观解释:
“并不是所有的x都有性质A’”与“存在x没有性质A”是一个意思。
不存在有性质A的X与“所有x都没有性质A’是一个意思。

例:令A(x)表示:x是天才，个体域: {我们班}
¬∀xA(x)表示:不是我们班所有同学都是天才。
∃x¬A(x)表示:我们班有些同学不是天才。
¬∃xA(x)表示:我们班没有同学是天才。
∀x¬A(x)表示:我们班所有同学都不是天才。
可见，这是符合我们思维习惯的。

量词作用域的扩充与收缩

量词辖域的扩充与收缩研究的是量词与∧∨的关系，其中一个运算对象不受该量词约束，有如下公式:


其它公式:

量词辖域的扩充和收缩，当只有一个运算对象受量词约束时，如果中间连接词时析取合取，加不加括号都没影响。如果中间连接词时蕴含，量词提前不说影响，但是上面这种情况注意，这里把则划开，是要加非的，∀xA(x)→B,等价于¬∀xA(x)∨B。比如：如果所有人都到齐了，我们就开会，等价于要么不是所有人都到期了，要么开会（说明都到齐了）。或者我们可以把非移动到量词符号的右边，量词变为存在两次，要么有人没来，要么开会。

量词的分配公式

若两个运算对象均受同一个量词约束，量词与“v，^”运算是什么关系?有如下的量词
分配公式:



可用公式1来证明公式2
举例说明公式3：




任意x合取（联想个体域消去），存在x析取都是等价分配，但是任意x析取，存在x合取都是只有蕴含关系。

前束范式

前束范式—所有量词都在公式前边。
前束范式的定义：
如果一个谓词公式符合下面条件，它就是前束范式：
所有量词前面都没有联接词;所有量词前面都没有联接词;所有量词的辖域都延伸到公式的末尾。

求前束范式的步骤:
1)消去公式中的联接词和->,<->(为了便于量词辖域的和扩充)
2)如果量词前有¬,用量词转化率将¬后移。
3)用约束变元的改名规则或自由变元的代入规则对变元换名(为量词辖域扩充做准备)。
4)用量词辖域扩充公式提取量词，使之成为前束范式的形式。

今天的文章离散数学谓词逻辑公式_离散数学思维导图分享到此就结束了，感谢您的阅读。