球形检验的定义_重复测量方差分析不符合球形检验

参考自维基百科
球形检验（Mauchly’s test of sphericity），适用于重复测量时检验不同测量之间的差值的方差是否相等，用于三次以及三次之上（想也能够想明白，两次重复测量根本就没有办法比较差值的方差，因为只有一个方差）。
例子：

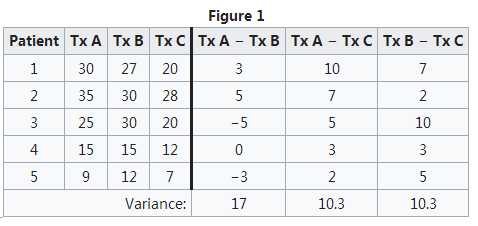
从方差看出，17可能与10.3差别很大，可能违背球形测试，所以我们要进行一下球形检验，看是否违背球形测试。
于是假设，

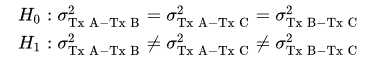
当球形检验的可能性大于等于alpha（一般设为0.05）时，接受H0，否则，拒绝H0。如果接受H0假设，那当然是最好的，如果不接受H0假设，就需要对自由度进行矫正。如果用SPSS进行处理时，会做出一个小于等于1的epsilon值，越小证明越违背球形假设。
SPSS中提到了三种方法，the Greenhouse-Geisser (1959), the Huynh-Feldt (1976), and the lower-bound，这三种矫正方法，各有利弊。
Girden提出了一种解决方案，当epsilon大于0.75的时候，采用the Huynh-Feldt进行矫正，若小于0.75或者不清楚时，可以采用the Greenhouse-Geisser。
我只是有点理解了简单大框，但是针对怎样用公式计算还是不清楚，各方资料只是说可以通过SPSS看到结果。若大家知道具体的方法，可以发出来，大家共同学习。

今天的文章球形检验的定义_重复测量方差分析不符合球形检验分享到此就结束了，感谢您的阅读。