手眼标定_机器人手眼标定详细步骤

转载请注明出处 https://blog.csdn.net/wanggao_1990/article/details/81435660

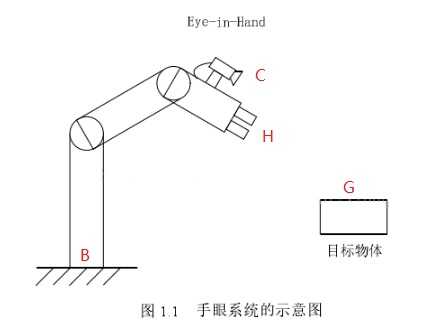
机器人视觉系统中要实现像素坐标与实际坐标的转换，首先要进行标定。这里标定不仅包括摄像头标定，也包括机器人系统的手眼标定。这里的构型为Eye-in-hand。

1、摄像机标定

（1）理论

张正友棋盘标定法对摄像机进行标定。
由于摄像机标定结果要用到后面的手眼标定中，棋盘图片拍摄时需要遵守：标定板固定位置不动，手眼组合体变换姿态拍摄图片。
目的：两组坐标系的两两转化矩阵：$T_1$和$T_2$
1） 摄像机坐标系C转化为图片像素坐标系P的转换矩阵T1

$P=T_1\ast C$

T1在摄像机标定中内参矩阵3*3
2） 棋盘世界坐标系G转化为摄像机坐标系C的转换矩阵T2

$C=T_2\ast G$

T2在摄像机标定中外参矩阵4*4，由旋转矩阵r33和平移向量t31构成[ t r; 0 0 0 1]

(2) 方法

OpenCv 或者 Matlab

2、手眼标定

（1）理论部分

手眼标定目的：得到机器手坐标系H转化为摄像机坐标系$C$的转化矩阵$T_3$。可表示为：

$C=T_3\ast H$

T3需要根据公式$AX=XB$得到；实际中，分别知道$A$、$B$求出来的X有无穷多个解。所以为了实现唯一解至少需要两组$A$和$B$，即至少需要3个位置的摄像机标定结果。
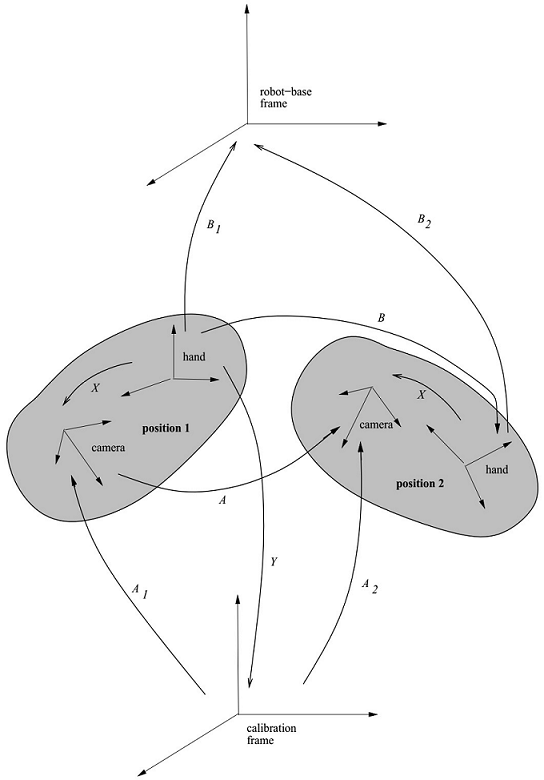
下图为$AX=XB$图解，棋盘相对机器人基坐标系固定，因此有

$B_1\ast X^{-1}\ast A_1=B_2\ast X^{-1}\ast A_2$

转换$A_2\ast A_1^{-1}\ast X=X\ast B_2^{-1}\ast B_1$

可令 $A=A_2\ast A_1^{-1}$，$B=B_2^{-1}\ast B_1$。

1) $A$的求法

$A$是两个摄像机坐标系之间的变换矩阵。假设上述摄像机标定中有3张标定图片的外参标定结果分别是$H_{c1}$、$H_{c2}$、$H_{c3}$，那么可以得到两个$A$矩阵：

$A_1=H_{c2}\ast H_{c1}^{-1}$

$A_2=H_{c3}\ast H_{c2}^{-1}$

2) $B$的求法

B是两个机器手坐标系之间的变换矩阵。假设上述摄像机标定中的3张标定图片所一一对应的机器手坐标系在基坐标系（也可以是工件坐标系或者其他固定的参考坐标系）中的坐标系描述矩阵结果分别是$H_{g1}$、$H_{g2}$、$H_{g3}$（需要从机器人控制器或示教器中读取或转换），那么可以得到两个$B$矩阵：

$B_1=H_{c2}^{-1}\ast H_{c1}$

$B_2=H_{c3}^{-1}\ast H_{c2}$

由以上两组$A$和$B$，代入$AX=XB$就可以得到唯一解X，从而$T_3=X$。
至少2组数据，可以进行求解，参考Navy_HandEye或Tsai_HandEye等方法。

（2）计算过程

1. 获取摄像机标定已知摄像机外参矩阵$H_{c1}$、$H_{c2}$、$H_{c3}$（摄像机标定时已有）

2. 从机器人控制器中读取对应的机械手坐标末端姿态描述数据
   机器人系统的坐标系描述数据可能有2种形式：
   – 平移向量+欧拉角: $x,y,z,r_z,r_y,r_z$ ， 需要知道转换关系.
   – 平移向量+四元数模式： $x,y,z,q_w,q_x,q_y,q_z$，唯一转换。
   推荐选择四元数模式，转换成旋转矩阵方式唯一，如下

   $R=\left[\begin{array}{ccc}2(q_w^2+q_x^2)-1& 2(q_x{q}_y-q_w{q}_z)& 2(q_x{q}_z+q_w{q}_x)\\ 2(q_x{q}_y+q_w{q}_z)& 2(q_w^2+q_y^2)-1& 2(q_y{q}_z-q_w{q}_x)\\ 2(q_x{q}_z+q_w{q}_x)& 2(q_y{q}_z+q_w{q}_x)& 2(q_w^2+q_z^2)-1\end{array}\right]$

3. 求解摄像机坐标系到机械手坐标系的变换矩阵X
   例如采集图像25幅，进行相机标定，可得到25个外参矩阵，同时对应可以从控制器界面读取或者转换得到25个姿态矩阵。接着可以利用 1） 2）得到$C_{25}^2$组$A$、$B$，再利用$AX=XB$计算得到$X$。

标题3、根据标定结果对目标定位

##（1）理论部分
由上述1、2标定得到：

基坐标系转化为像素坐标系的变换矩阵，可由下面两式求解（注意使用齐次坐标系）。

$z_c\ast [u,v,1{]}^T=H_{pc}\ast [x_c,y_c,z_c{]}^T$

$[x,y,z{]}^T=H_g\ast H_{cg}^{-1}\ast [x_c,y_c,z_c{]}^T$

未完 …

win10，vs2015。 linux下使用有几个小错误或警告地方，根据编译器输出略作修改。源码 https://github.com/wanggao1990/HandEyeCalibration， 有用烦请star一下。

新浪演示视频地址 http://t.cn/RDW1sAf?m=4271991789966178&u=2335487824，CSDN视频 https://live.csdn.net/v/177543

opencv4.1 也加入了手眼标定，可以尝试。

今天的文章手眼标定_机器人手眼标定详细步骤分享到此就结束了，感谢您的阅读。