lasso回归的解_适合做lasso回归的数据「建议收藏」

Lasso(Least absolute shrinkage and selection operator)方法是以缩小变量集（降阶）为思想的压缩估计方法。它通过构造一个惩罚函数，可以将变量的系数进行压缩并使某些回归系数变为0，进而达到变量选择的目的。

正则化

正则化（Regularizaiton）是一种防止过拟合的方法。

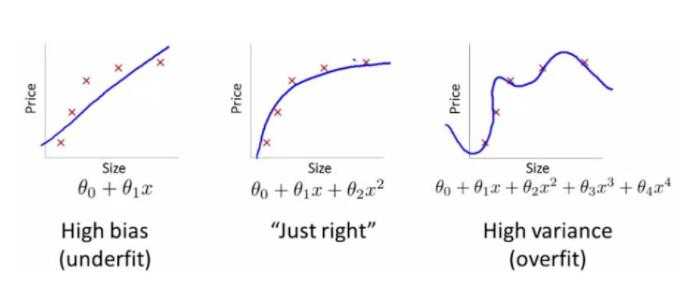
图1 欠拟合与过拟合

图来自：百度百科（过拟合）

从图中可以看出，最右边的属于一种过拟合，过拟合的问题通常发生在变量（特征）过多的时候，这种情况下训练出的方程总是能很好的拟合训练数据，也就是损失函数可能非常接近于 0 或者就为 0。但是，这样的曲线会导致它无法泛化到新的数据样本中。

如果解决过拟合问题?

（1）尽量减少选取变量的数量

可以人工检查每一项变量，并以此来确定哪些变量更为重要，保留那些更为重要的特征变量。这种做法非常有效，但是其缺点是当舍弃一部分特征变量时，也舍弃了问题中的一些信息。例如，所有的特征变量对于预测房价都是有用的，实际上并不想舍弃一些信息或者说舍弃这些特征变量。

（2）正则化

在正则化中将保留所有的特征变量，但是会减小特征变量的数量级。当有很多特征变量时，其中每一个变量都能对预测产生一点影响。假设在房价预测的例子中，可以有很多特征变量，其中每一个变量都是有用的，因此不希望把任何一个变量删掉，这就导致了正则化概念的发生。

如果应用正则化去解决实际问题？

在图1中，可以看出最右边的是过拟合的，但是不想抛弃 $\theta_{3}\theta_{4}$ 变量自带的信息，因此加上惩罚项，使得 $\theta_{3}\theta_{4}$ 足够小。

优化目标为：

$\min _{\theta} \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}$

在优化目标的基础上，添加一些项（惩罚项），如下：

$\min _{\theta} \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+1000 \theta_{3}^{2}+1000 \theta_{4}^{2}$

1000 只是随便写的一个表示很大的数字。现在，如果想要最小化这个函数，那么为了最小化这个新的损失函数，就要让 $\theta_{3}$ 和 $\theta_{4}$ 尽可能小。因为，如果在原有代价函数的基础上加上 $1000 \theta_{3}^{2}+1000 \theta_{4}^{2}$ 这一项，那么这个新的代价函数将变得很大，所以，当最小化这个新的代价函数时， $\theta_{3}$ 和 $\theta_{4}$ 尽可能小或者接近于0，就像我们忽略了这两个值一样。如果做到这一点（ $\theta_{3}$ 和 $\theta_{4}$ 接近于0），那么我们将得到一个近似的二次函数，并且 $h_{\theta}$ 中并没有丢失 $\theta_{3}$ 和 $\theta_{4}$ 的信息（虽然 $\theta_{3}$ 和 $\theta_{4}$ 接近于0，但是还是存在的）

但是在真实问题中，一个预测问题可能有上百种特征，并不知道哪一些是高阶多项式的项，就像不知道 $\theta_{3}$ 和 $\theta_{4}$ 是高阶的项。所以，如果假设有一百个特征，并不知道如何选择关联度更好的参数，如何缩小参数的数目等等。因此在正则化里，要做的事情，就是把减小损失函数中所有的参数值，（因为并不知道是哪一个或哪几个是要去缩小的）。

因此，我们需要修改代价函数，变成如下形式：

$\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]$

其中 $\lambda \sum_{j=1}^{n} \theta_{j}^{2}$ 就是正则化项； λ称为正则化参数，作用是控平衡拟合训练的目标和保持参数值较小。

Lasso回归模型

Lasso回归是在损失函数后，加L1正则化，如下所示：

$\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+ \lambda \sum_{j=1}^{k}\left|w_{j}\right|\right]$

m为样本个数，k为参数个数，其中 $\lambda \sum_{j=1}^{k}\left|w_{j}|\right$ 为L1正则化。

此外：还有L2正则化： $\lambda \sum_{j=1}^{n} w_{j}^{2}$ ，加了这种正则化的损失函数模型为：脊(岭)回归（Ridge Regression）。

为什么Lasso可以做降维？

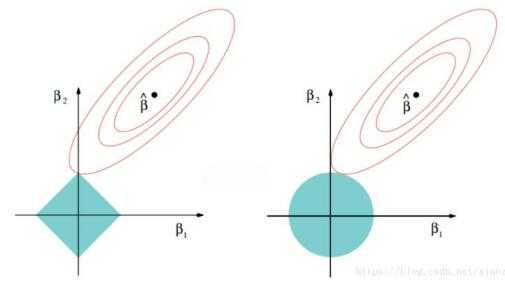
图2

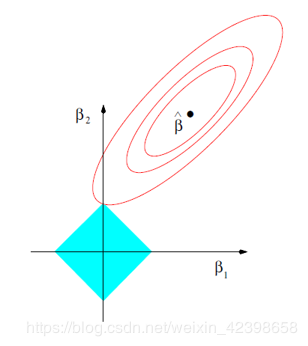
以二维数据空间为例，说明Lasso和Ridge两种方法的差异，左图对应于Lasso方法，右图对应于Ridge方法。

如上图所示，两个图是对应于两种方法的等高线与约束域。红色的椭圆代表的是随着λ的变化所得到的残差平方和，βˆ为椭圆的中心点，为对应普通线性模型的最小二乘估计。左右两个图的区别在于约束域，即对应的蓝色区域。

等高线和约束域的切点就是目标函数的最优解，Ridge方法对应的约束域是圆，其切点只会存在于圆周上，不会与坐标轴相切，则在任一维度上的取值都不为0，因此没有稀疏；对于Lasso方法,其约束域是正方形，会存在与坐标轴的切点，使得部分维度特征权重为0，因此很容易产生稀疏的结果。

所以，Lasso方法可以达到变量选择的效果，将不显著的变量系数压缩至0，而Ridge方法虽然也对原本的系数进行了一定程度的压缩，但是任一系数都不会压缩至0，最终模型保留了所有的变量。

以二维空间为例，约束域在L1中，为 $|\beta _{1}|+|\beta _{2}|=1$ ，对应左图蓝色。

约束域在L2中，为 ${\beta_{1}}^{2}+{\beta_{2}}^{2}=1$ ，对应左图蓝色。

由图也可以看出，Lasso的复杂程度由λ来控制，λ越大对变量较多的线性模型的惩罚力度就越大，从而最终获得一个变量较少的模型。

上述参考：回归问题-Lasso回归

参数求解

但是Lasso回归有一个很大的问题，就是由于L1正则化项用的是绝对值之和，导致损失函数有不可导的点。也就是说，梯度下降法等优化算法对它统统失效了。

那怎么才能求损失函数极小值呢？接下来介绍两种全新的求极值解法：坐标轴下降法（coordinate descent）和最小角回归法（ Least Angle Regression， LARS）

（1）坐标轴下降法

坐标轴下降法顾名思义，是沿着坐标轴的方向去下降，这和梯度下降不同。梯度下降是沿着梯度的负方向下降。不过梯度下降和坐标轴下降的共性就都是迭代法，通过启发式的方式一步步迭代求解函数的最小值。

坐标轴下降法的数学依据主要是如下的这个结论：

一个可微的凸函数J(θ)，其中θ是nx1的向量，即有n个维度。如果在某一点 ${\theta}'$ ，使得J(θ)在每一个坐标轴 ${\theta}'_{i}$ (i=1,2,..,n)上都是最小值，那么 $J({\theta }'_{i})$ 就是一个全局的最小值。于是优化目标就是在θ的n个坐标轴上(或者说向量的方向上)对损失函数做迭代的下降，当所有的坐标轴上的 ${\theta }'_{i}$ 都达到收敛时，损失函数最小，此时的θ即为要求的结果。

具体的算法过程：

（1）把θ向量随机取一个初值。记为 ${\theta_{0}}^{0}$ ，上面的括号里面的数字代表我们迭代的轮数，当前初始轮数为0。

（2）对于第k轮的迭代，我们从 ${\theta_{1}}^{k}$ 开始，到 ${\theta_{n}}^{k}$ 为止，依次求 ${\theta_{i}}^{k}$ ，其中 ${\theta_{i}}^{k}$ 的表达式如下：

${\theta_{i}}^{k}=argmin J({\theta_{1}}^{k},{\theta_{2}}^{k},..,{\theta_{i-1}}^{k},{\theta_{i}},{\theta_{i+1}}^{k-1},...,{\theta_{n}}^{k-1})$ 也就是说 ${\theta_{i}}^{k}$ 是使 $J(\theta )$ 最小化时候的 $\theta _{i}$ 值。此时J(θ)只有 ${\theta_{i}}^{k}$ 是变量，其余均为常量，因此最小值容易通过求导求得。

（3）检查 $\theta^{k}$ 向量和 $\theta^{k-1}$ 向量在各个维度上的变化情况，如果在所有维度上变化都足够小，那么 $\theta^{k}$ 即为最终结果，否则转入2，继续第k+1轮的迭代。

此外，SVM中对于带有惩罚项的软间隔问题，利用的就是此种思想：序列最小优化算法（SMO）。

（2）最小角回归法

预备算法：A.前向选择（Forward Selection）算法。

前向选择算法的原理是是一种典型的贪心算法。要解决的问题是对于:

　　　 $Y=X \theta$ 这样的线性关系，如何求解系数向量θ的问题。其中Y为 m*1的向量，X为m*n的矩阵，θ为n*1的向量。m为样本数量，n为特征维度。

　　　把矩阵X看做n个m*1的向量 $X_{i}$ (i=1,2,…n)，在Y的X变量 $X_{i}$ (i=1,2,…n)中，选择和目标Y最为接近的一个变量 $X_{k}$ ，（余弦值的绝对值小，夹角小，则最为接近）用 $X_{k}$ 来逼近Y，得到下式：

　　　　 $\bar{Y}=X_{k} \theta_{k}$

　　　　其中： $\theta_{\mathbf{k}}=\frac{\left\langle\mathbf{X}_{\mathbf{k}} \mathbf{Y}\right\rangle} {{\left\|\mathbf{X}_{\mathbf{k}}\right\|_{2}}^{2}}$

<>表示两向量的内积，下面是向量 $X_{k}$ 二范数的平方，简单来说就是 $X_{k}$ 的模长的平方，因为 $\left \| X \right \|_{2} =\sqrt{\sum_{i=1}^{n} {X_{i}}^{2}}$

　　　　即： $\bar{Y}$ 是 Y在 $X_{k}$ 上的投影。那么，可以定义残差(residual)： $Y_{diff} =Y-\bar{Y}$ 。由于是投影，所以很容易知道 $Y_{diff}$ 和 $X_{k}$ 是正交的。再以 $Y_{diff}$ 为新的因变量，去掉 $X_{k}$ 后，剩下的自变量的集合 $X_{i}$ (i=1,2,3…i−1,i+1,…n)为新的自变量集合，重复刚才投影和残差的操作，直到残差为0，或者所有的自变量都用完了，才停止算法。

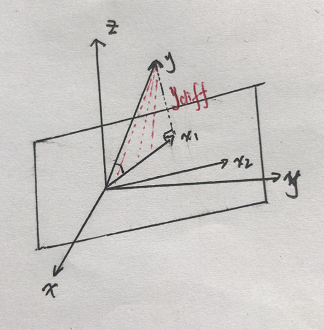
当X只有2维时，例子如上图，和Y最接近的是 $X_{1}$ ，首先在 $X_{1}$ 上面投影，残差如上图(1)长虚线。此时 $X_{1}* \theta_{1}$ 模拟了Y， $\theta_{1}$ 模拟了θ(仅仅模拟了一个维度)。接着发现最接近的是 $X_{2}$ ，此时用残差(Y’)接着在 $X_{2}$ 投影，残差如图中短虚线。由于没有其他自变量了，此时 $X_{1}* \theta_{1}+X_{2}* \theta_{2}$ 模拟了Y，对应的模拟了两个维度的θ即为最终结果。

此算法对每个变量只需要执行一次操作，效率高，速度快。但也容易看出，当自变量不是正交的时候，由于每次都是在做投影，所有算法只能给出一个局部近似解。因此，这个简单的算法太粗糙。

B.前向梯度（Forward Stagewise）算法

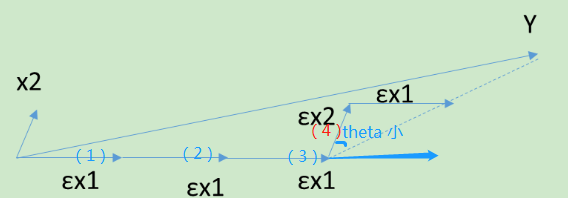
前向梯度算法和前向选择算法有类似的地方，但是前向梯度算法不是粗暴的用投影，而是每次在最为接近的自变量 $X_{t}$ 的方向移动一小步，然后再看残差 $Y_{diff}$ 和哪个 $X_{i}$ (i=1,2,…n)最为接近。此时我们也不会把 $X_{t}$ 去除，因为我们只是前进了一小步，有可能下面最接近的自变量还是 $X_{t}$ 。如此进行下去，直到残差 $Y_{diff}$ 减小到足够小，算法停止。

当X只有2维时，例子如上图，和Y最接近的是，首先在 $X_{1}$ 上面走一小段距离，此处ε为一个较小的常量，发现此时的残差还是和 $X_{1}$ 最接近。那么接着沿 $X_{1}$ 走，一直走到发现残差不是和 $X_{1}$ 最接近，而是和 $X_{2}$ 最接近(夹角小)。接着沿着 $X_{2}$ 走一小步，发现残差此时又和 $X_{1}$ 最接近，那么开始沿着 $X_{1}$ 走，走完一步后发现残差为0，那么算法停止。此时Y由刚才所有的所有步相加而模拟，对应的算出的系数θ即为最终结果。

　　　　当算法在ε很小的时候，可以很精确的给出最优解，当然，其计算的迭代次数也是大大的增加。和前向选择算法相比，前向梯度算法更加精确，但是更加复杂。

　　　　最小角回归法(Least Angle Regression， LARS）就是一种折中的方法，可以综合前向梯度算法和前向选择算法的优点，保留了前向梯度算法一定程度的精确性，同时简化了前向梯度算法一步步迭代的过程。　

最小角回归过程如下：

首先，还是找到与因变量Y最接近或者相关度最高的自变量 $X_{k}$ ，使用类似于前向梯度算法中的残差计算方法，得到新的目标 $Y_{diff}$ ，此时不用和前向梯度算法一样小步小步的走。而是直接向前走直到出现一个 $X_{t}$ ，使得 $X_{t}$ 和 $Y_{diff}$ 的相关度和 $X_{k}$ 与 $Y_{diff}$ 的相关度是一样的，此时残差 $Y_{diff}$ 就在 $X_{t}$ 和 $X_{k}$ 的角平分线方向上，此时我们开始沿着这个残差角平分线走，直到出现第三个特征 $X_{p}$ 和 $Y_{diff}$ 的相关度足够大的时候，即 $X_{p}$ 到当前残差 $Y_{diff}$ 的相关度和 $\theta_{k}$ 、 $\theta_{t}$ 与 $Y_{diff}$ 的一样。将其也叫入到Y的逼近特征集合中，并用Y的逼近特征集合的共同角分线，作为新的逼近方向。以此循环，直到 $Y_{diff}$ 足够的小，或者说所有的变量都已经取完了，算法停止。此时对应的系数θ即为最终结果。

当θ只有2维时，例子如上图，和Y最接近的是 $X_{1}$ ，首先在 $X_{1}$ 上面走一段距离，一直到残差在 $X_{1}$ 和 $X_{2}$ 的角平分线（红色的 ${\theta}'$ 与蓝色的 ${\theta}'$ 相等）上，此时沿着角平分线走，直到残差最够小时停止，此时对应的系数β即为最终结果。

　　　　最小角回归法是一个适用于高维数据的回归算法，其主要的优点有：

　　　　1）特别适合于特征维度n 远高于样本数m的情况。

　　　　2）算法的最坏计算复杂度和最小二乘法类似，但是其计算速度几乎和前向选择算法一样

　　　　3）可以产生分段线性结果的完整路径，这在模型的交叉验证中极为有用

　　　　主要的缺点是：

　　　　由于LARS的迭代方向是根据目标的残差而定，所以该算法对样本的噪声极为敏感。

以上是刘建平老师博客的主要内容，详见：https://www.cnblogs.com/pinard/p/6018889.html

关于LARS与Lasso回归关系，

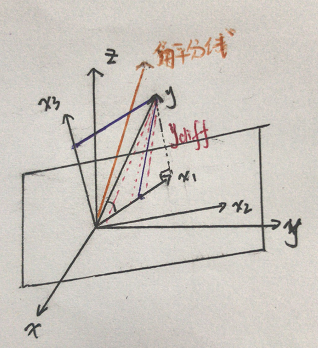
用下面的图，从数学角度，进一步解释LARS。

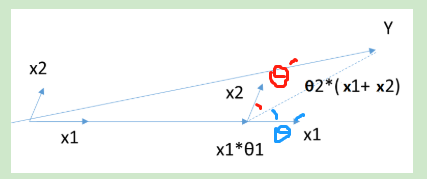
如上图所示，如果把 $X_{1}$ 单独选出来就和Y形成一个线性回归问题，那它肯定有最小二乘解，最小二乘解就是过Y往 $X_{1}$ 直线上做一条垂线，交于这个点，那这个点就是只有参与了这个线性回归问题的最小二乘解的位置。从原点出发，向着这个局部的最小二乘解出发，在前进的时候，我们每走到的一个点和Y都会形成一个残差向量（图中红色的标志），残差向量一边会变化，如果最后走到最小二乘解这一点时，残差和 $X_{1}$ 垂直，所以残差向量变成了垂线，此时他与 $X_{1}$ 之间的相关系数为零。

在前进的过程里，把 $X_{i}$ (i=2,3…n)对应的样本变量也跟 $Y_{diff}$ 做内积，求他们之间的相关系数，当 $X_{1}$ 跟 $Y_{diff}$ 的相关系数越来越小时，总有某一个时刻，另外有一个变量（可能） $X_{k}$ 与 $Y_{diff}$ 的相关系数与 $X_{1}$ 跟 $Y_{diff}$ 的相关系数相同，（图中k=3）。此时，这个变量 $X_{3}$ 加进来，加进来之后，我们的前进方向就要修正（沿着角平分线的方向继续）。

当往角平分线的方向前进时，无论是 $X_{1}$ 还是 $X_{3}$ ，残差与两者的相关系数一定会同时变化，继续往最小二乘解方向走，走到一定程度，相关系数会越来越小，即残差向量和角平分线越来越垂直，这时可能加入第三个变量 $X_{2}$ ， $X_{2}$ 和 $Y_{diff}$ 的相关系数会在增大，追上 $X_{1}$ 与 $Y_{diff}$ 的相关系数，此时再把 $X_{2}$ 加进去，找上一次的角平分线（橙色的那个线）和 $X_{2}$ 的角平分线。如此类推，每一次都是顺着角平分方向前进时，一定可以把所有的变量加进去，然后前进到一个点，这个点就是残差向量和其他所有变量所形成的样本变量的相关系数为零（夹角90°），即残差向量垂直与所有的 $X_{i}$ (i=1,2,3…n)垂直与这个平面，最后求得最小二乘解。

上述过程，可以用下面公式这个公式表达，

$X_{j}^{T}(y-X \theta)=\gamma \cdot s_{j}, \forall j \in \mathrm{A}$

$(y-X \theta)$ 是残差，A是样本集，每一次都是从样本集中选择一个 $X_{j}$ ，通过求解内积来选定，一旦内积完成在游走时，符号（正负号）一般不会变，只会改变內积的大小， $\gamma$ 为内积， $s_{j}$ 就是符号函数（大于0等于1，小于0等于-1）。

而Lasso回归如下：

$loss = \frac{1}{2} \sum_{i=1}^{m}\left(y_{i}-w^{\top} x_{i}\right)^{2}+\lambda \sum_{i=1}^{n}\left|w_{i}\right|$

由于涉及到了绝对值问题，所以求解参数过程如下：

$loss =\frac{1}{2}\left\|\left[\begin{array}{c}{y_{1}-w^{T} x_{1}} \\ {y_{2}-w^{T} x_{2}} \\ {\cdots} \\ {y_{m}-w^{T} x_{m}}\end{array}\right]\right\|^{2}+\lambda \sum_{i=1}^{n}\left|w_{i}\right|$

$=\frac{1}{2}\left\|\left[\begin{array}{c}{y_{1}} \\ {y_{2}} \\ {\cdots} \\ {y_{m}}\end{array}\right]-w^{T}\left[\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\cdots} \\ {x_{m}}\end{array}\right]\right\|^{2}+\lambda \sum_{i=1}^{n}\left|w_{i}\right|$

$=\frac{1}{2}\left\|y-w^{T} X\right\|^{2}+\lambda \sum_{i=1}^{n}\left|w_{i}\right|=\frac{1}{2}\left(y-w^{T} x\right)^{T}\left(y-w^{T} x\right)+\lambda \sum_{i=1}^{n}\left|w_{i}\right|$

由于 $w_{i}$ 正负无法确定，因此将 $\lambda \sum_{i=1}^{n}\left|w_{i}\right|$ 转换成 $\lambda \sum_{i=1}^{N} w_{i} \cdot \operatorname{sign}\left(w_{i}\right)$ 再进行求导，其中 $\operatorname{sign}\left(w_{i}\right)$ 为符号函数。

对loss求导有：

$\frac{\partial J(w)}{\partial w}=\frac{1}{2} \frac{\partial}{\partial w}\left(\left(y-w^{T} x\right)^{T}\left(y-w^{T} x\right)\right)+\frac{\partial}{\partial w}\lambda \sum_{i=1}^{N} w_{i} \cdot \operatorname{sign}\left(w_{i}\right)$

$=\frac{1}{2} \frac{\partial}{\partial w}\left((y-X w)^{T}(y-X w)\right)+\lambda \operatorname{sign}\left(w_{i}\right)$

$\begin{array}{l}{=\frac{1}{2} \frac{\partial}{\partial w}\left(w^{T} X^{T} X w-2 w^{T} X y+y^{T} y\right)} +\lambda \operatorname{sign}\left(w_{i}\right)\\ {=\frac{1}{2}\left(X^{T} X w+X^{T} X w-2 X y\right)}+\lambda \operatorname{sign}\left(w_{i}\right) \\ {=X^{T} X w-X y}+\lambda \operatorname{sign}\left(w_{i}\right)\end{array}$

令 $\frac{\partial J(w)}{\partial w}=0$ ，有 $X_{j}^{T}(y-X w) = \lambda \cdot \operatorname{sign}\left(w_{j}\right)$ （1）

到这里可以发现最终w满足的方程式和LARS很像，不同的是符号函数的情况，这也是导致差异的原因。我们知道得到公式（1）的前提是对上式的求导，但是都满足可导吗？请看下图：

发现除了约束条件的四个顶点不可导以外，其他均可导，不可导的情况就是某一个 $\beta$ 为0，这也是是解释了为什么产生跳跃的原因。

基于上述原因，将LARS做修正，就可以用在Lasso里面，即如果有一个非零系数（ $\beta$ ）变为零，那么直接将这个变量淘汰，LARS修正算法和lasso就一样了。

今天的文章lasso回归的解_适合做lasso回归的数据「建议收藏」分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/71569.html