参考:
1. https://www.zybuluo.com/lutingting/note/554459
2. 《数字图像处理的MATLAB实现(第二版)》, Rafael C. Gonzalez
3. MATLAB帮助文档
Hough变换于1962年由Paul Hough提出,是一种使用表决方式的参数估计技术,其原理是利用图像空间和Hough参数空间的线-点对偶性,把图像空间中的检测问题转换到参数空间中进行。
下面参考https://www.zybuluo.com/lutingting/note/554459
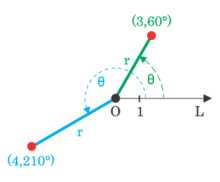
1. 极坐标系
极坐标系(polar coordinates)是指在平面内由极点O、极轴L、极径r组成的坐标系。如下图展示了一个极坐标系,图中两个红点是要利用极坐标表示的两个点,黑点是极坐标系的极点。
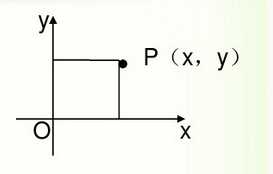
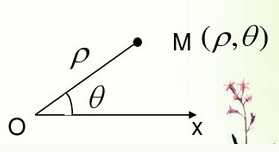
2. 极坐标系和直角坐标系的关系
在直角坐标系下,点P的坐标表示为
在极坐标系下,点M的坐标表示为
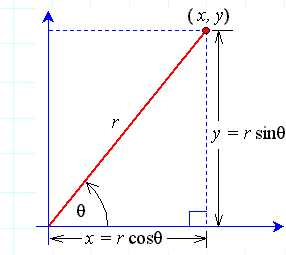
可以根据下图对极坐标和直角坐标进行相互之间的转换
注:本图中的r与上图中的ρ是同样的表述
3. 极坐标系和直角坐标系中的直线
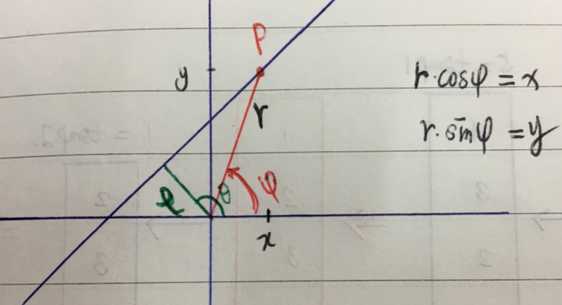
在极坐标系中,应该如何表示直线方程呢?如上图所示,有一直线L,点P是直线L上的任意一点,其对应的直角坐标为(x,y),该点的极坐标为(r,φ),该直线到原点O的距离为ρ。
首先,由图可知:ρ = r * cos( θ – φ ),然后根据三角函数的关系对该式展开,可得:
ρ = r * cos( θ – φ ) = r * cosθcosφ + r * sinθsinφ
又根据点P的直角坐标(x,y)和极坐标(r,φ)之间的关系:x=r*cosφ, y=r*sinφ,代入到上式中,可以得到ρ=xcosθ+ysinθ。
所以直线L的极坐标方程就是ρ=xcosθ+ysinθ。
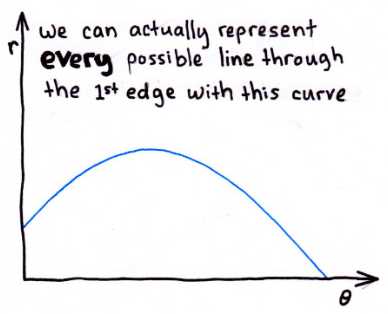
上式中(x,y)是直线L上的任意一点。也就是说,给出极坐标系中的一个点(ρ,θ),可以唯一确定直角坐标系中的一条直线,其中ρ表示直角坐标系下直线到原点O的距离,θ表示直角坐标系下直线和原点间的垂线与x轴正向的夹角。或者说,直角坐标系中的直线在极坐标系下表示为一个点。这即是极坐标系和直角坐标系的点-线对偶性。
4. 利用Hough变换检测直线
下面的例子形象地展示了如何利用Hough变换进行直线检测。记住上面的结论:直角坐标系中的一条直线对应于极坐标系下的一个点。这里的直角坐标系对应于原始图像空间,极坐标系对应于参数空间(也叫Hough空间)。
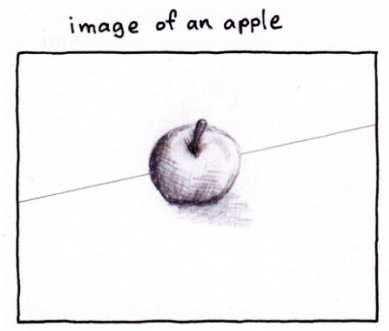
· 给定一幅图像,如下所示,图像中有一条直线
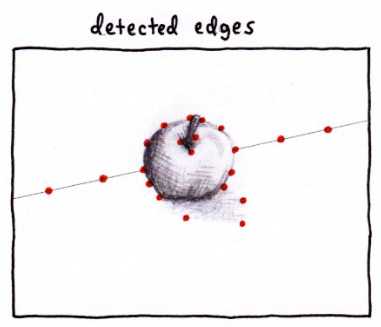
· 首先进行边缘检测,找出边缘点,如下图所示,红色的点表示边缘点
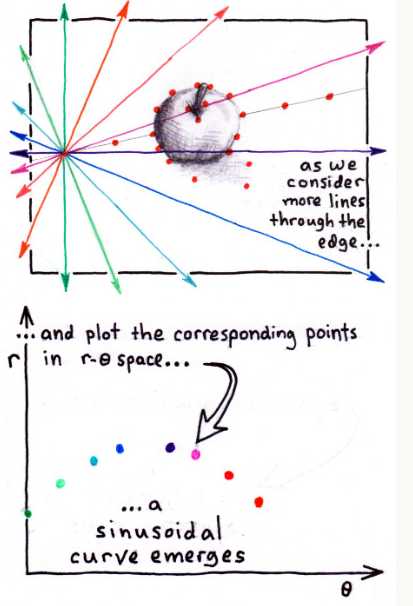
· 对于任何一个边缘点,找到所有可能经过该点的直线,这些直线都各自对应着参数空间中的一个点,而该边缘点的无穷多条直线对应于参数空间中的点将形成一条参数空间中的曲线。如下左边两图所示,原始图像空间中绿色的直线在参数空间中对应的点是(r2,θ2),原始图像空间中蓝色的直线在参数空间中对应的点是(r1,θ1)。如下右边两图所示,找出经过该边缘点的所有直线,列出各直线在参数空间中的点,这些点可以连接成一条曲线。
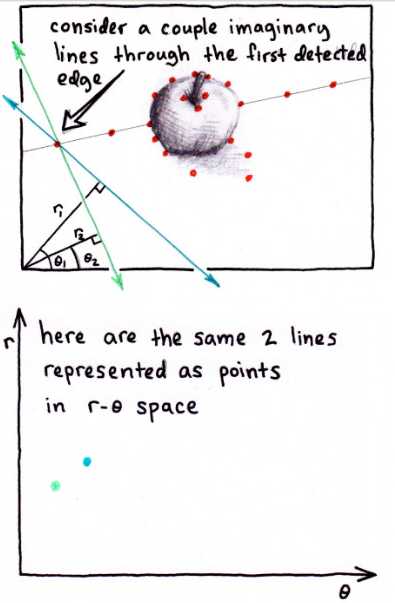
· 曲线如下图所示,最终我们可以用这条曲线来表示所有可能经过第1个边缘点的直线
· 重复上述过程,画出所有边缘点的曲线,每个边缘点都对应着参数空间中的一条曲线。那么,参数空间中所有这些曲线的交点一定是原始图像空间中所有边缘点的共同直线。或者说某个交点经过的曲线最多(此处涉及到表决,如何判断这个交点经过的曲线最多),那么这个交点很有可能表示原始图像中的直线。得到这个交点的坐标(ρ,θ)之后,根据方程ρ=xcosθ+ysinθ,可以计算出直角坐标系下的直线,然后在原始图像中标出直线,达到检测直线的目的。
下面参考《数字图像处理的MATLAB实现(第二版)》
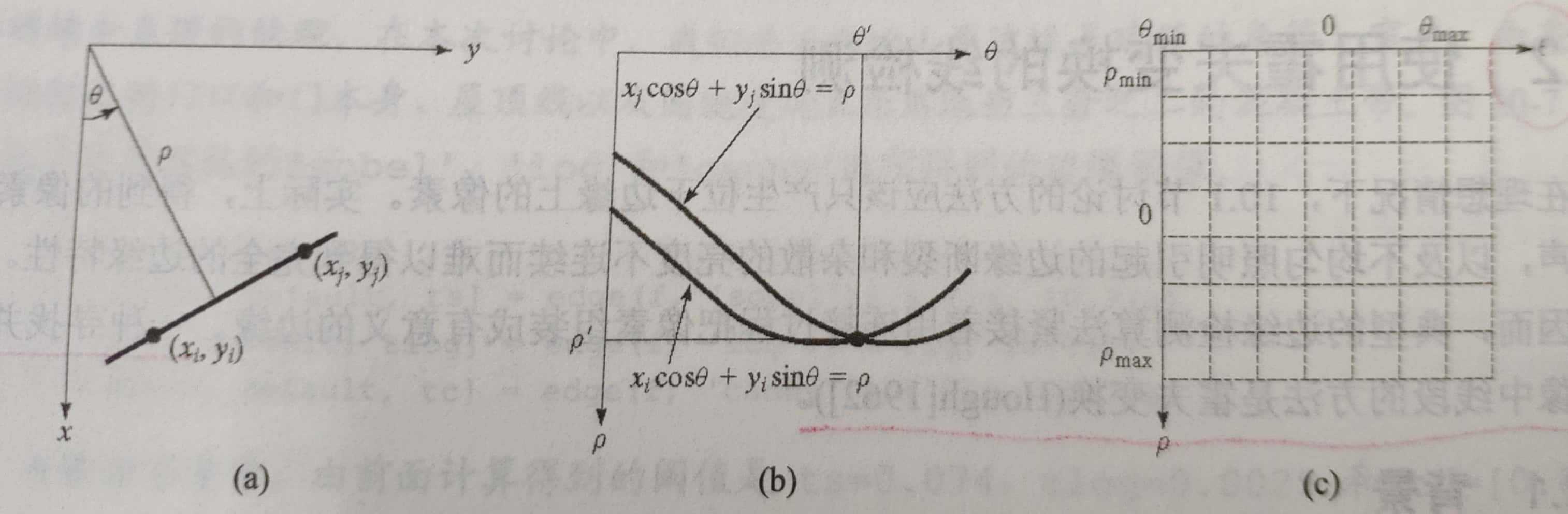
如上图所示。图a说明了参数ρ和θ的几何解释。水平线的θ=0,ρ等于正的x截距;相似的,垂直线θ=90°,ρ等于正的y截距。或者θ=-90°,ρ等于负的y截距。
图b中的两条曲线分别表示通过图a中两个特定点(xi, yi)和(xj, yj)的一簇直线。交叉点对应于通过(xi, yi)和(xj, yj)的直线。
Hough变换在计算上的诱人之处是把ρθ空间再细分为所谓的累加单元。正如上图c中说明的那样,其中的(ρmin, ρmax)和(θmin, θmax)是预期的参数值范围。一般来说,值的最大范围是-90°≤θ≤90°和-D≤ρ≤D,其中D是图像中两个角之间的最远距离。
图c中,在坐标(i,j)的单元位置,累加器的值是A(i,j),对应于参数空间坐标(ρi,θj)的小正方形。最初,这些单元位置均为0。然后,对于原始图像空间中的每个非背景点(xk,yk)(图a中),我们令θ等于在θ轴上允许的细分值,并通过公式ρ=xk*cosθ+yk*sinθ解出相应的ρ值。然后,得到的ρ值四舍五入为最接近的ρ轴上允许的单元值。相应的累加器单元增加一个增量。在这个过程的最后,累加单元A(i,j)中的值Q表示参数空间中的点(ρi, θj)有Q条曲线经过,对应到原始图像空间中,也就是有Q个点是在一条相同的直线上的。在ρθ平面上,细分的数目决定了这些点共线的精确度。累加器数组在工具箱中叫做Hough变换矩阵,简称Hough变换。
与Hough变换有关的工具箱函数
图像处理工具箱中提供了3个与Hough变换相关的函数。函数hough()实现了前面讨论的概念;函数houghpeaks()寻找Hough变换的峰值(累加单元的高计数);函数houghlines()以来自其他两个函数的结果为基础在原始图像中提取线段。
1. 函数hough()
默认语法是: [ H, theta, rho ] = hough(f)
完整语法是: [ H , theta, rho ] = hough(f, ‘ThetaRes’, val1, ‘RhoRes’, val2)
其中,H是Hough变换矩阵,theta(单位是度数)和rho是θ和ρ向量,在这些值上产生Hough变换。输入f是二值图像,val1是0到90的标量,指定了沿θ轴Hough变换的间距(默认是1),val2是0到hypot(size(f,1), size(f,2))之间的实标量,其中函数hypot()表示平方和的平方根,指定了沿ρ轴Hough变换的间隔(默认是1)。
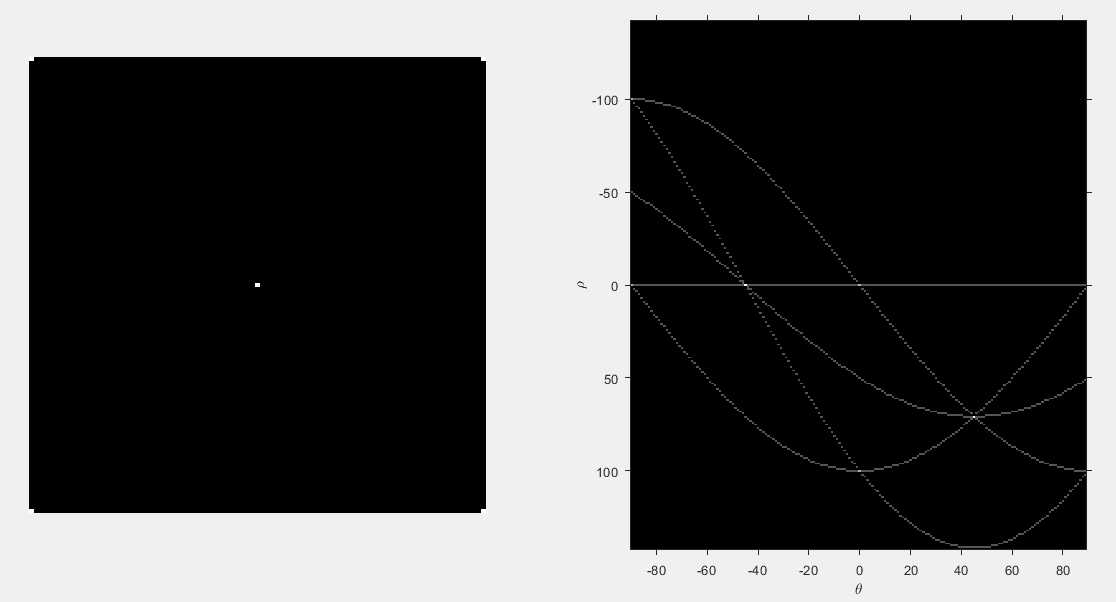
举例:hough变换的说明,在这个例子中,我们用简单的合成图像来说明hough函数的机理。
% 创建合成图像
f = zeros(101, 101);
f(1, 1) = 1;
f(101, 1) = 1;
f(1, 101) = 1;
f(101, 101) = 1;
f(51, 51) = 1;
% 显示合成图像
figure;
subplot(121), imshow(f);
% 采用默认值进行hough变换,并显示hough变换的结果
H = hough(f);
subplot(122), imshow(H, []);接下来,我们调用带有三个参数的hough函数。然后把向量theta和rho作为附加输入参量传递给函数imshow(),从而控制水平轴和垂直轴的标度。我们还要把 ‘InitialMagnification’ 选项传递给带有值 ‘fit’ 的imshow函数,因此整个图像将被强迫在图形窗口中进行装配。axis函数被用来打开轴标记,并使其显示填充图的矩形框。最后,xlabel和ylabel函数用希腊字母LaTeX字体符号在轴上标值。
% 创建合成图像
f = zeros(101, 101);
f(1, 1) = 1;
f(101, 1) = 1;
f(1, 101) = 1;
f(101, 101) = 1;
f(51, 51) = 1;
% 显示合成图像
figure;
subplot(121), imshow(f);
% 采用完整语法形式调用hough函数
[ H, theta, rho ] = hough(f, 'ThetaRes', 1, 'RhoRes', 1);
subplot(122), imshow(H, [], 'XData', theta, 'YData', rho, 'InitialMagnification', 'fit');
axis on;
axis normal;
xlabel('\theta'); % 加上\后x坐标轴显示θ,否则显示theta
ylabel('\rho');接下来分析一下上图,左图为原始图像空间,有5个目标点,右图为参数空间,有5条对应的曲线。三条曲线(直线可视为曲线)在±45°处的有交点,说明在原始图像空间中在±45°处各有3个点共线。两条曲线在(ρ,θ)=(0,-90)、(-101,-90)、(0,0)、(101,90)、(0,90)处有交点,说明原始图像空间中有4组位于垂直线和水平线上的共线点。
2. 函数houghpeaks()
线检测和线连接用的Hough变换,第一步是用高的计数寻找累加单元(工具箱中把高的计数单元作为峰值)。
函数作用:确定Hough变换中的峰值(identify peaks in hough transform)
语法形式:
peaks = houghpeaks(H, numpeaks) 或者 peaks = houghpeaks(…, Name, Value, …)
描述:
peaks = houghpeaks(H, numpeaks) locates peaks in the Hough transform matrix, H, generated by the hough function. 参数 numpeaks 指定了需要确定的峰值个数。函数返回 peaks,它是一个包含峰值点行坐标和列坐标的矩阵(从后面示例代码中可知,这个矩阵是一个两列矩阵,第一列保存的是ρ,第二列保存的是θ)。peaks = houghpeaks(…, Name, Value, …) locates peaks in the Hough transform matrix, 这里使用命名的参数控制各项操作。
MATLAB帮助文档中的示例:(为了更直观地显示处理效果,代码有改动)
locate and display peaks in hough transform of rotated image ( 定位并显示旋转图像的hough变换中的峰值点 )
close all; clear all; clc;
% Read image into workspace
I = imread('circuit.tif');
figure;
subplot(121), imshow(I);
% Create binary image
BW = edge(imrotate(I, 50, 'crop'), 'canny');
subplot(122), imshow(BW);
% Create hough transform of image
[H, theta, rho] = hough(BW);
figure, imshow(H, [], 'InitialMagnification', 'fit');
axis normal;
% Find peaks in the hough transform of the image and plot them
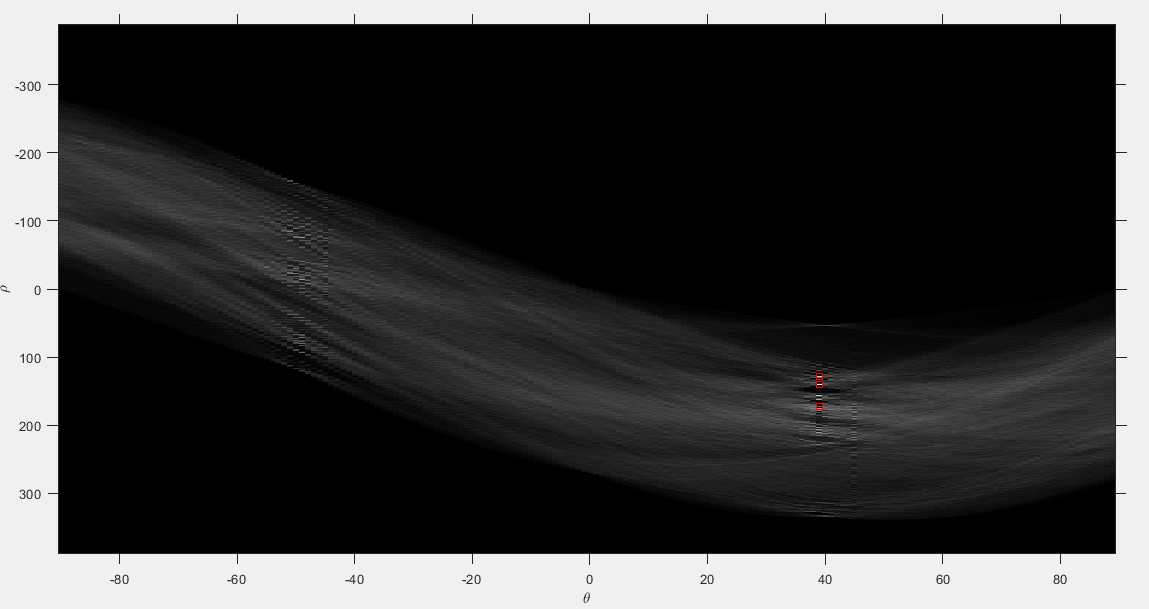
P = houghpeaks(H, 3);
figure, imshow(H, [], 'XData', theta, 'YData', rho, 'InitialMagnification', 'fit');
xlabel('\theta'), ylabel('\rho');
axis on, axis normal, hold on;
plot(theta(P(:, 2)), rho(P(:, 1)), 's', 'color', 'red'); 
在图像中找出了3个峰值点,均用红色矩形框标记出来了。
3. 函数houghlines()
函数作用:
根据Hough变换提取线段(extract line segments based on hough transform)
语法形式:
lines=houghlines(BW, theta, rho, peaks)
lines=houghlines(…, Name, Value, …)
描述:
lines=houghlines(BW, theta, rho, peaks)提取图像BW中对应于Hough变换下特定峰点的线段(extract line segments in the image BW associated with particular bins in a Hough transform)。(这里把bin理解为hough变换中的峰点,不知道确不确切)。theta和rho是由函数hough()返回的向量。peaks是函数houghpeaks()返回的用于寻找线段的矩阵,该矩阵包含了Hough变换下特定峰点的行坐标和列坐标。返回值lines是一个结构数组,它的长度等于寻找到的线段的数量。
lines=houghlines(…, Name, Value, …)提取图像BW中的线段,这里命名的参数会影响函数的操作。(额,翻译过来就是这个样子)。
MATLAB帮助文档中的示例:(稍有改动)
Find line segments and Highlight longest segment(寻找线段并使最长的线段高亮)
close all; clear all; clc;
% Read image into workspace
I = imread('circuit.tif');
figure;
subplot(131), imshow(I);
% Rotate the image
rotI = imrotate(I, 33, 'crop');
subplot(132), imshow(rotI);
% Create a binary image
BW = edge(rotI, 'canny');
subplot(133), imshow(BW);
% Create the hough transform using the binary image
[H, T, R] = hough(BW);
figure, imshow(H, [], 'XData', T, 'YData', R, 'InitialMagnification', 'fit');
xlabel('\theta'), ylabel('\rho');
axis on, axis normal, hold on;
colormap(gca, hot);
% Find peaks in the hough transform of the image
P = houghpeaks(H, 5);
x = T(P(:,2));
y = R(P(:,1));
plot(x, y, 's', 'color', 'blue');
% Find lines and plot them
lines = houghlines(BW, T, R, P, 'FillGap', 5, 'MinLength', 7);
figure, imshow(rotI), hold on;
max_len = 0;
for k = 1 : length(lines) % here length(lines)=12
xy = [lines(k).point1; lines(k).point2];
plot(xy(:, 1), xy(:, 2), 'LineWidth', 2, 'Color', 'green');
% Plot beginnings and ends of lines
plot(xy(1,1), xy(1,2), 'x', 'LineWidth', 2, 'Color', 'yellow');
plot(xy(2,1), xy(2,2), 'x', 'LineWidth', 2, 'Color', 'red');
% Determine the endpoints of the longest line segment
len = norm(lines(k).point1 - lines(k).point2); % distance between point1 and point2
if ( len > max_len )
max_len = len;
xy_long = xy;
end
end
% Highlinght the longest line segment by coloring it cyan
plot(xy_long(:, 1), xy_long(:, 2), 'LineWidth', 2, 'Color', 'cyan'); 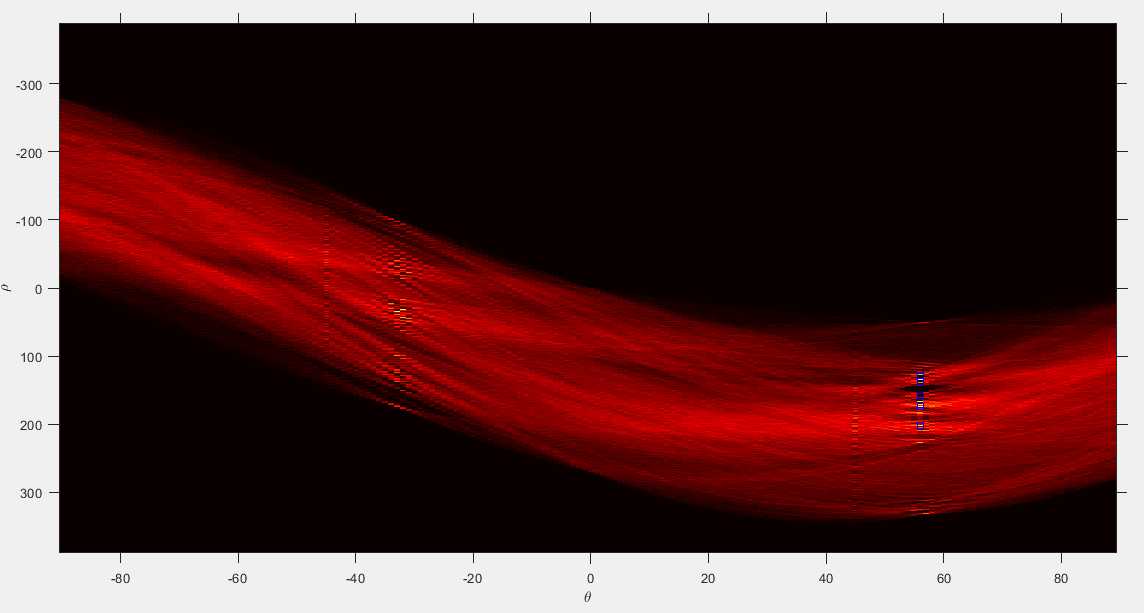
今天的文章数字图像处理中hough变换的原理_传统图像处理算法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/72400.html