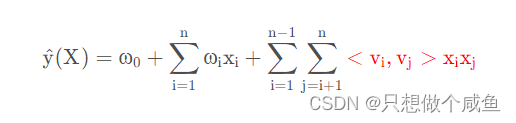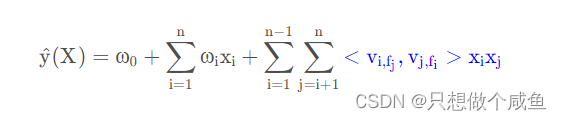最终幻想灰机wiki_ffm是什么意思

一、前言

FFM在FM的基础上进一步改进，在模型中引入类别的概念，即field。将同一个field的特征单独进行one-hot，因此在FFM中，每一维特征都会针对其他特征的每个field，分别学习一个隐变量，该隐变量不仅与特征相关，也与field相关。通过引入field的概念，FFM把相同性质的特征归于同一个field。

二、FFM模型

在说FFM之前，最好先了解下FM模型 

Factorization Machines（FM）：发展过程、原理及实现_只想做个咸鱼的博客-CSDN博客

 文章中提到FM的公式：

 红色两项，分别代表用隐向量内积表示权重系数矩阵，特征的交叉组合

FM存在的问题就是模型在进行特征表示时，是与所有的特征进行组合，即它对所有的特征组合时所用的表示都是一样的，至少也得权衡各个类别里面的交互特征学到，意味着不同的特征应该所表示的不同，例如男和北京、男和篮球，而男与另外两个特征组合时所用的表示是一样，这体现不出他们的不同和重要性

引出FFM的数学表达式：

 可以看到蓝色的隐向量部分多了fj和fi这就是添加的域表示，也可以等同额外添加了另一组隐向量，用来表示特征域的概念，用以区分特征与特征之间的区别，用来增强模型的表示。

三、代码实现

class FFM_Node(object):
    '''
    通常x是高维稀疏向量，所以用链表来表示一个x，链表上的每个节点是个3元组(j,f,v)
    '''
    __slots__ = ['j', 'f', 'v']    # 按照元组不是字典的方式存储类的成员属性
    
    def __init__(self, j, f, v):
        """
            j: Feature index (0-n-1)
            f: field index(0-m-1)
            v: value
        """
        self.j = j
        self.f = f
        self.v = v
    
class FFM(object):
    def __init__(self, m, n, k, eta, lambd):
        """
            m: Number of fields
            n: Number of features
            k: Number of latent factors
            eta: learning rate
            lambd: regularization coefficient
        """
        self.m = m
        self.n = n
        self.k = k
        
        #超参数
        self.eta = eta
        self.lambd = lambd
        
        # 初始化三维权重矩阵w~U(0, 1/sqrt(k))
        self.w = np.random.rand(n, m, k) / math.sqrt(k)
        
        # 初始化累积梯度平方和， AdaGrad时要用到
        self.G = np.ones(shape=(n, m, k), dtype=np.float64)
        self.log = Logistic()
    
    # 这个是计算第三项
    def phi(self, node_list):
        """
        特征组合式的线性加权求和
        param node_list: 用链表存储x中的非0值
        """
        z = 0.0
        for a in range(len(node_list)):
            node1 = node_list[a]
            j1 = node1.j
            f1 = node1.f
            v1 = node1.v
            for b in range(a+1, len(node_list)):
                node2 = node_list[b]
                j2 = node2.j
                f2 = node2.f
                v2 = node2.v
                w1 = self.w[j1, f2]
                w2 = self.w[j2, f1]
                z += np.dot(w1, w2) * v1 * v2
        
        return z
    
    
    def predict(self, node_list):
        """
        输入x， 预测y的值
        """
        z = self.phi(node_list)
        y = self.log.decide_by_tanh(z)
        return y

    # 随机梯度下降
    def sgd(self, node_list, y):
        """
        根据一个样本更新模型参数：
        node_list: 链表存储x中的非0值
        y: 正样本1， 负样本-1
        """
        kappa = -y / (1+math.exp(y*self.phi(node_list)))    # 论文里面的那个导数
        for a in range(len(node_list)):
            node1 = node_list[a]
            j1 = node1.j
            f1 = node1.f
            v1 = node1.v
            for b in range(a+1, len(node_list)):
                node2 = node_list[b]
                j2 = node2.j
                f2 = node2.f
                v2 = node2.v
                c = kappa * v1 * v2      # 这是求导数
                
                # self.w[j1,f2]和self.w[j2,f1]是向量，导致g_j1_f2和g_j2_f1也是向量
                g_j1_f2 = self.lambd * self.w[j1, f2] + c * self.w[j2, f1]
                g_j2_f1 = self.lambd * self.w[j2, f1] + c * self.w[j1, f2]
                
                # 计算各个维度上的梯度累积平方和
                self.G[j1, f2] += g_j1_f2 ** 2
                self.G[j2, f1] += g_j2_f1 ** 2
                
                # Adagrad 算法
                self.w[j1, f2] -= self.eta / np.sqrt(self.G[j1, f2]) * g_j1_f2  # sqrt(G)作为分母，所以G必须是大于0的正数
                self.w[j2, f1] -= self.eta / np.sqrt(
                    self.G[j2, f1]) * g_j2_f1  # math.sqrt()只能接收一个数字作为参数，而numpy.sqrt()可以接收一个array作为参数，表示对array中的每个元素分别开方
    
    # 训练
    def train(self, sample_generator, max_echo, max_r2):
        """
        根据一堆样本训练模型
        sample_generator: 样本生成器，每次yield (node_list, y)，node_list中存储的是x的非0值。通常x要事先做好归一化，即模长为1，这样精度会略微高一点
        max_echo: 最大迭代次数
        max_r2: 拟合系数r2达到阈值时即可终止学习
        """
        for itr in range(max_echo):
            print("echo: ", itr)
            y_sum = 0.0
            y_sqare_sum = 0.0
            err_square_sum = 0.0    # 误差平方和
            population = 0   # 样本总数
            for node_list, y in sample_generator:
                y = 0.0  if y == -1 else y    # 真实的y取值为{-1,1}，而预测的y位于(0,1)，计算拟合效果时需要进行统一
                self.sgd(node_list, y)
                y_hat = self.predict(node_list)
                y_sum += y
                y_sqare_sum += y ** 2
                err_square_sum += (y-y_hat) ** 2
                population += 1
            
            var_y = y_sqare_sum - y_sum * y_sum / population  # y的方差
            r2 = 1 - err_square_sum / var_y
            print("r2: ", r2)
            if r2 > max_r2:
                print("r2 have reach", r2)
                break
        
    # 模型保存
    def save_model(self, outfile):
        '''
        序列化模型
        :param outfile:
        :return:
        '''
        np.save(outfile, self.w)

    def load_model(self, infile):
        '''
        加载模型
        :param infile:
        :return:
        '''
        self.w = np.load(infile)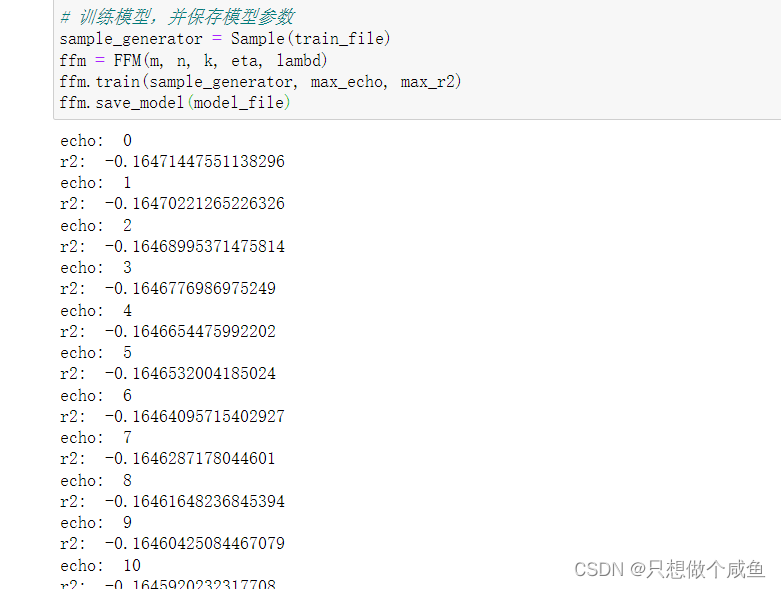

数据集很小，只是验证模型能跑否这个就暂时到这了

四、总结

1、FM是FFM的特例
FFM在FM的基础上提出了field的概念，FM模型中每个特征只有一个隐向量，而FFM则有多个隐向量，点乘时根据对应field进行选择
从算复杂度来看，FM通过化简可以将复杂度降到O(kn)，而FFM则是O(kn^2)
2、FFM优缺点

FFM优点：
增加field的概念，同一特征针对不同field使用不同隐向量，模型建模更加准确
FFM缺点：
计算复杂度比较高，参数个数为nfk，计算复杂度为O(kn2)

这代码实现部分较为潦草，知道核心思想，添加域的表示即可，

接下来就开始不如深度学习与推荐系统的碰撞了.
 

今天的文章最终幻想灰机wiki_ffm是什么意思分享到此就结束了，感谢您的阅读。