TopN问题_topos theory

什么是TopN问题：给定一个很大的数据量n，要求从n中提取出最大/最小/重复频度最高的N个数（N相对于n较小，如n为10亿量级，而N为100）。

求top N 在大数据中很常见，主要思路有三种：

       1. 先排序，在遍历出最大或最小的N个

       2. 通过大小堆，维持一个N个大小的堆，每次和堆顶元素比较，在堆化

       3. 中位数的中位数算法BFPRT

第一种，先排序，排序算法有很多，冒泡排序，快速排序等。时间复杂度是 O(n*log n)，这里不详讲。

第二种， 用大小堆，维持一个大小堆，元素个数是N个，遍历数据，和堆顶元素比较，在把堆，堆化，堆化的复杂度是log N,总的时间复杂度是O(n * log N) , N 一般远远小于n，所以比第一种时间复杂度小，效率比第一个方法高。

第三种，中位数的中位数方法，为什么说是中位数的中位数算法BFPRT呢，听起来比较拗口。它的时间复杂度是O(n),  比用大小堆的时间复杂度小，如果N比较小，用堆也是不错的选择，毕竟BFPRT的时间复杂度n的系数也不小。

解决这个问题，很容易想到要使用排序算法，首先，使用方法1笨办法 – 全部排序，解出来再说。

1. 将n个数全部排序

   使用普通排序，将n个数全部排序之后，取出最大的k个，即为所得。

   时间复杂度：O(n*lg(n))

   分析 & 优化思路：明明只需要TopN，却将全局都排序了，这也是这个方法复杂度非常高的原因。那能不能不全局排序，而只局部排序呢?这就引出了第二个优化方法。

2. 只将TopN 个数排序

   使用冒泡排序

   时间复杂度：O(n*k)

   分析：冒泡，将全局排序优化为了局部排序，非TopN 的元素是不需要排序的，节省了计算资源。不少朋友会想到，需求是TopN ，是不是这最大的N 个元素也不需要排序呢?这就引出了第三个优化方法。

3. 把TopN 和非TopN 分为两类，均不排序

   使用堆排序，只找到TopN ，不排序TopN 

   时间复杂度：O(n*lg(N))

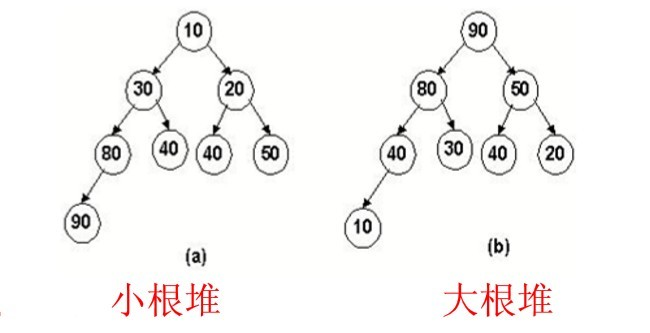
   分析：堆，将冒泡的TopN 排序优化为了TopN 不排序，节省了计算资源。堆，是求TopN 的经典算法。  最小N个值：利用大顶堆 ，     最大N个值：利用小顶堆。

   最大堆和最小堆是二叉堆的两种形式。

   最大堆：根结点的键值是所有堆结点键值中最大者，且每个结点的值都比其孩子的值大。

   最小堆：根结点的键值是所有堆结点键值中最小者，且每个结点的值都比其孩子的值小。

4. 

5. JDK中PriorityQueue实现了数据结构堆，通过指定comparator字段来表示小顶堆或大顶堆，默认为null，表示自然序（natural ordering）。

public int findKthLargest(int[] nums, int k) {
  PriorityQueue<Integer> minQueue = new PriorityQueue<>(k);
  for (int num : nums) {
    if (minQueue.size() < k || num > minQueue.peek())
      minQueue.offer(num);
    if (minQueue.size() > k)
      minQueue.poll();
  }
  return minQueue.peek();
}

或者：首先，我们需要构建一个大小为N的小顶堆，小顶堆的性质如下：每一个父节点的值都小于左右孩子节点，然后依次从文件中读取10亿个整数，如果元素比堆顶小，则跳过不进行任何操作，如果比堆顶大，则把堆顶元素替换掉，并重新构建小顶堆。当10亿个整数遍历完成后，堆内元素就是TopN的结果。

public class TopN {
    public static int N = 10;           //Top10
    public static int LEN = 100000000; //1亿个整数
    public static int arrs[] =  new int[LEN];
    public static int arr[] = new int[N];
    //数组长度
    public static int len = arr.length;
    //堆中元素的有效元素 heapSize<=len
    public static int heapSize = len;
    public static void main(String[] args) {
        //生成随机数组
       for(int i = 0;i<LEN;i++){
           arrs[i] = new  Random().nextInt(999999999);
       }
 
       //构建初始堆
       for(int i =  0;i<N;i++){
           arr[i] = arrs[i];
       }
       //构建小顶堆
        long start =System.currentTimeMillis();
       buildMinHeap();
       for(int i = N;i<LEN;i++){
           if(arrs[i] > arr[0]){
               arr[0] = arrs[i];
               minHeap(0);
           }
       }
        System.out.println(LEN+"个数，求Top"+N+"，耗时"+(System.currentTimeMillis()-start)+"毫秒");
       print();
    }
 
 
    /**
     * 自底向上构建小堆
     */
    public static void buildMinHeap(){
        int size = len / 2;
        for(int i = size;i>=0;i--){
            minHeap(i);
        }
    }
 
    /**
     * i节点为根及子树是一个小堆
     * @param i
     */
    public static void minHeap(int i){
        int l = left(i);
        int r = right(i);
        int index = i;
        if(l<heapSize && arr[l]<arr[index]){
            index = l;
        }
        if(r<heapSize && arr[r]<arr[index]){
            index = r;
        }
        if(index != i){
            int t = arr[index];
            arr[index] = arr[i];
            arr[i] = t;
            //递归向下构建堆
            minHeap(index);
        }
    }
 
    /**
     * 返回i节点的左孩子
     * @param i
     * @return
     */
    public static int left(int i){
        return 2*i;
    }
 
    /**
     * 返回i节点的右孩子
     * @param i
     * @return
     */
    public static int right(int i){
        return 2*i+1;
    }
    /**
     * 打印
     */
    public  static void print(){
        for(int a:arr){
            System.out.print(a+",");
        }
        System.out.println();
    }

快排 – 随机选择算法 Quick – Select

对只分两类不排序的进一步优化 – 堆排序需要遍历，而partition只需要遍历其中一个分支。

TopN是希望求出arr[1,n]中最大的k个数，那如果找到了第N大的数，做一次partition，不就一次性找到最大的N个数了么?

画外音：即partition后左半区的N个数。

问题变成了arr[1, n]中找到第N大的数。

再回过头来看看第一次partition，划分之后：

i = partition(arr, 1, n); 

• 如果i大于N，则说明arr[i]左边的元素都大于N，于是只递归arr[1, i-1]里第N大的元素即可;
• 如果i小于N，则说明说明第k大的元素在arr[i]的右边，于是只递归arr[i+1, n]里第N-i大的元素即可;

这就是随机选择算法randomized_select，RS，其伪代码如下：

int RS(arr, low, high, k){ 
  if(low== high) return arr[low]; 
  i= partition(arr, low, high); 
  temp= i-low; //数组前半部分元素个数 
  if(temp>=k) 
      return RS(arr, low, i-1, k); //求前半部分第k大 
  else 
      return RS(arr, i+1, high, k-i); //求后半部分第k-i大 
} 

Quick – Select的Java实现

public int findKthLargest(int[] nums, int k) {
  return quickSelect(nums, k, 0, nums.length - 1);
}

// quick select to find the kth-largest element
public int quickSelect(int[] arr, int k, int left, int right) {
  if (left == right) return arr[right];
  int index = partition(arr, left, right);
  if (index - left + 1 > k)
    return quickSelect(arr, k, left, index - 1);
  else if (index - left + 1 == k)
    return arr[index];
  else
    return quickSelect(arr, k - index + left - 1, index + 1, right);

}

今天的文章TopN问题_topos theory分享到此就结束了，感谢您的阅读。