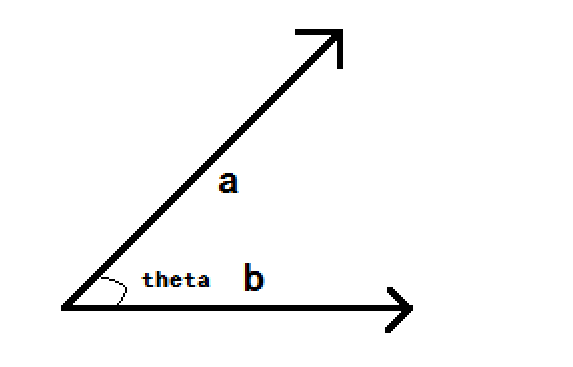
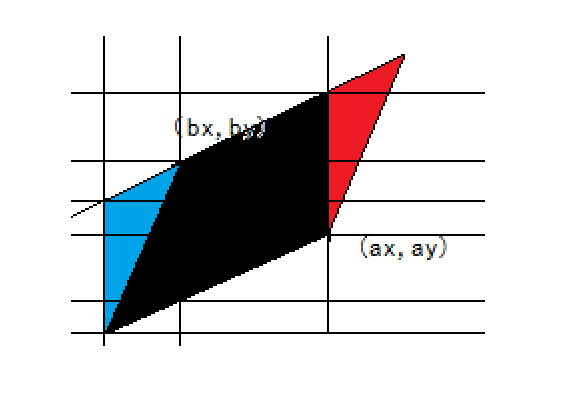向量的矢量积计算_空间单位向量的计算公式

编程小号 • 2024-04-09 20:06 • 未分类

如果已知向量 $\overrightarrow{a}$ 和向量 $\overrightarrow{b}$ ，以及他们之间的夹角 $\theta$ ，那么按照定义它们之间的矢量积数值大小为：

$\left | \overrightarrow{a}\times \overrightarrow{b} \right |=\left|\overrightarrow{a}\right|\cdot \left|\overrightarrow{b}\right|\cdot sin\theta$ ，其方向根据右手定则指向屏幕的内部。

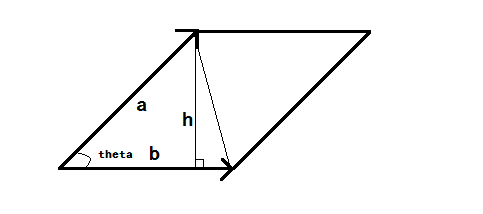
这个结果的数值大小等于平行四边形的面积，理由如下：

$S_\Delta=\frac{1}{2}*b*h=\frac{1}{2}*b*a*sin\theta$

$S_{sqare}=2S_\Delta=a\cdot b\cdot sin\theta$

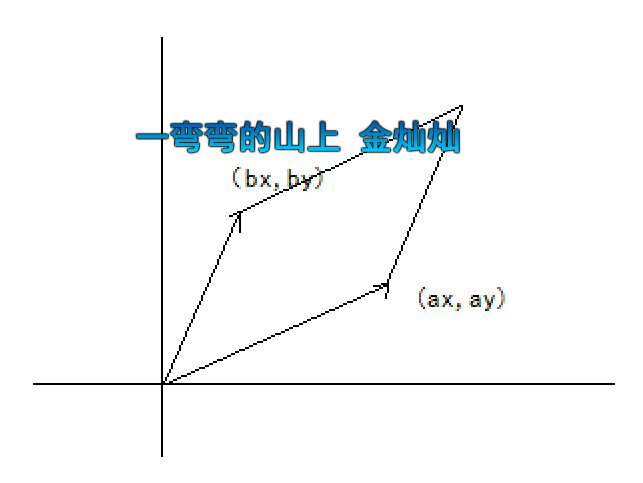
如果已知向量a和向量b的坐标分别为和，那结果如下：

$\overrightarrow{a}\times \overrightarrow{b} =(a_x \overrightarrow{i} +a_y\overrightarrow{j})\times(b_x \overrightarrow{i} +b_y\overrightarrow{j})$

$\overrightarrow{a}\times \overrightarrow{b} =a_xb_y\overrightarrow{i}\times\overrightarrow{j}+a_yb_x\overrightarrow{j}\times\overrightarrow{i}$

$\left | \overrightarrow{a}\times \overrightarrow{b} \right |=a_xb_y-a_yb_x$

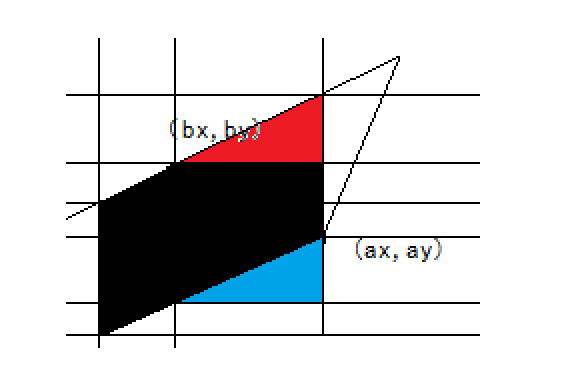
另一方面从作图法研究一遍，看看怎么直接求平行四边形的面积：

将红色区域用蓝色替换

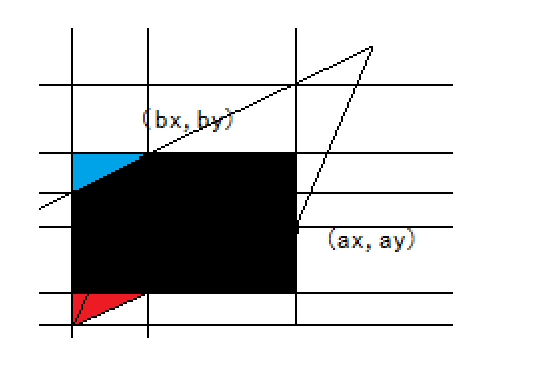
继续将红色区域用蓝色替换

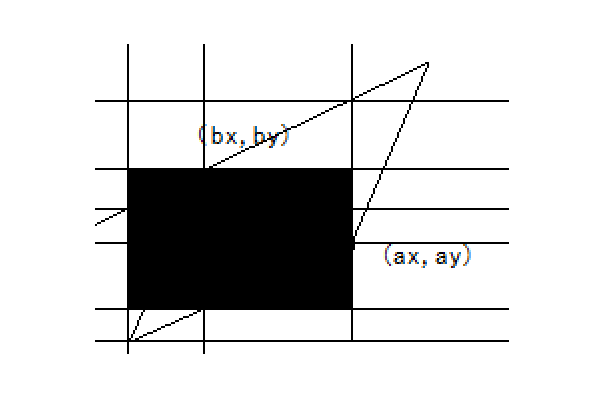
于是最后的结果如下

今天的文章向量的矢量积计算_空间单位向量的计算公式分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/74413.html

向量的矢量积计算_空间单位向量的计算公式

相关推荐

发表回复