python符号用法_python绘制图形

在实际进行数学运算的时候，其实有两种运算模式，一种是数值运算，一种是符号运算（代数）。而我们日常使用计算机进行数值运算，尤其是比如除、开平方等运算时，往往只能得到其近似值（一般通过扩大精度来缩小误差），最终总会已一定的误差，如果使用符号运算模式，则可以完全避免此种问题，符号运算可极大的避免在需要大量运算过程中，造成的累积性误差问题。

当然，符号计算体系（代数），还可以做比如多项式合并、展开、求极限、求和、多重求和、求导、求积分等等工作，如果能熟练运用，会为工作和计算效率带来极大提升。

本文只讲述日常常用的操作和知识。

一、数学符号及符号表达式

符号（代数）表达式，区别于常规的数值型数学表达式，常规数学表达式，比如x+y*2等，基本x和y是一个变量，且变量最终也会被赋值，由变量组成的表达式，最后得出的也是一个数值。

而符号表达式，则真正的由符号组成，而符号无需提前赋值，由符号组成的表达式，最终也是一个符号型表达式，并不会得出一个数值。

1.1 定义符号及函数

1.1.1 定义符号

符号计算的前提是，必须有符号，而在Python中，想用一个变量时，必须提前定义，此处的定义，区别于数值型，不是进行赋值，只是简单的定义一个符号，后续会用这个符号与其他符号一起组成符号表达式。

#以下两种方式均可以定义符号
#1、symbols函数定义
from sympy import symbols
x,y,z=symbols('x y z') #该表达式定义了x、y、x三个符号，注意symbols函数接收的是字符串，需定义的多个符号之间需要有 空格隔开

#2、直接导入sympy内置的符号
from sympy.abc import x,y #该表达式直接导入了x、y两个符号，如果需要定义非英文字母的字符变量，比如gender等，则只能使用第一种方式

1.1.2 定义函数

#后续在进行求导、积分等运算时，会用到大量函数表达的形式，sympy同时也提供了声明函数的方法
#sympy之所以相对于符号又单独提出函数的形式，主要是为了后面求解微积分及方程时，让代码更加直观
f=sympy.Function('f')
#或者
f=symbols('f',function=True)
#或者
from sympy import Function
f=symbols('f',cls=Function)
f(t) #即定义了一个自变量为t的f函数，做如此声明，主要是让表达式变的更加直观，其实f(t)本质还是f，即代表一个符号表达式

1.2 符号运算符

符号或代数表达式，一般由运算符将符号、初等函数、超越函数等连接起来组成，以下为常见的符号运算符：

运算符	说明	示意
+	加：两个多和符号相加
–	减：两个或多个符号相减
*	乘：两个或多个符号相乘
/	除：两个或多个符号相除
**	幂：某个符号的指数（幂运算）	**3→
Eq(exp1,exp2)	等：等号表达式，也叫等式，或者方程式，标示exp1=exp2，比如x+y=3，默认exp2=0 取等式的左半部分：eq.lhs 取等式的右半部分：eq.rhs	$Eq(x+2y+9)\rightarrow x+2y+9=0$ $Eq(x+2y,9)\rightarrow x+2y=9$

1.3 sympy常用内置符号

常用内置符号
符号	说明	示意
sympy.I	虚数单位i
sympy.E	自然对数的底e
sympy.oo	无穷大oo
sympy.pi	pi

1.4 常用初等符号运算函数

以下函数，返回的结果均为符号形式，即未转化为数值，如果想要数值，可使用evalf函数将符号形式转化为数值形式

初等函数	说明	示意
sympy.log(x,a)	对数函数，其中a为底数，其中a默认为，即数学上的Ln（x）	，
exp()	某个符号的自然指数，e指数函数	→
a**x	指数函数，其中a为底数	，
sympy.sqrt(x)	求平方根函数	$\sqrt{x}$ ， $\sqrt{2}$
x**a	幂函数，其中a为幂	$x^{a}$ ，，，
sympy.root(x,a)	求x的a次方根	$\sqrt[a]{x}$ ， $\sqrt[3]{8}$
sympy.factorial(a)	求a的阶乘
sympy.sin、cos、tan、cot	正弦、余弦、正切、余切函数等超越函数	$\sin (x)$ 、 $\cos (x)$ 、 $\tan (x)$ 、 $\cot (x)$
sympy.asin、acos、atan、acot	反正弦、余弦、正切、余切等函数	asin(x) acos(x)

1.5 求和(数列累加)函数

1.5.1 概述

#累加求和函数，也是初等数学中，比较重要的运算或运算符号，一般是从求某指定数列的累加时首次接触
#求和需使用sympy.summation函数，其与sum函数的区别是，sum求传入多个值的合，summation求某个表达式，符号取指定区间内值，逐个计算结果并累加求和，可以认为是求积分的初等形式
sympy.summation(
    f, #含有指定符号的表达式
    *symbols, #元组格式，传入需迭代求值的符号，符号的取值返回（x,1,n）
    **kwargs #元组，一般不需要，也可以元组形式，传入指定符号的取值范围（x,1,n）,（n,1,100）,即进行双重求和
)

1.5.2 累加求和∑

#当只需要求符号本身在指定区间取值范围内，对应符号表达式合的结果，则是最基本的求和,符号上则是∑
#1、如果求和最终有确定值，则会返回对应求和结果值
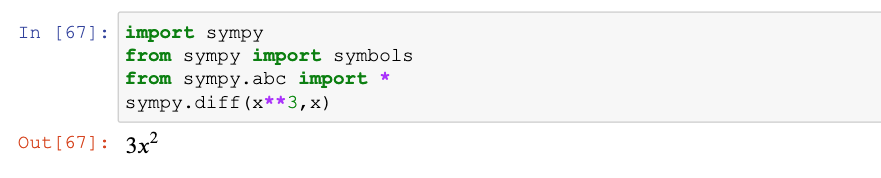
import sympy
from sympy.abc import *
f= (1/2)**n
sympy.summation(f,(n,0,sympy.oo)) #如下左图所示

#2、如果求和最终没有确定值，则会返回求和表达式
import sympy
from sympy.abc import *
f= 1/sympy.log(n) +3
sympy.summation(f,(n,0,sympy.oo)) #如下右图所示

求和公式： $\sum_{n=0}^{oo}(\frac{1}{2})^n$ 计算过程如下：求和公式： $\sum_{n=0}^{oo}\frac{1}{log(n)}+3$ 计算过程如下：

1.5.3 双重累加求和∑∑

#当如果符号对应的取值区间，也是一个变量时，则此时叫双重累加求和
#比如，求表达式f(n),n在(0,m)之间、同时m在(0,100)之间的累加和，此时，相当于需针对m在其取值区间内每个值，分别迭代求f(n)在（0，m）之间的值，对应符号为∑∑
import sympy 
from sympy.abc import *
f=2*n+1
sympy.summation(f,(n,0,m),(m,0,100)) #运算结果如下

双重求和公式： $\sum_{m=0}^{1000}\sum_{n=0}^{m}(2n+1)$ 计算过程如下：

1.6 精确表达和处理有理数

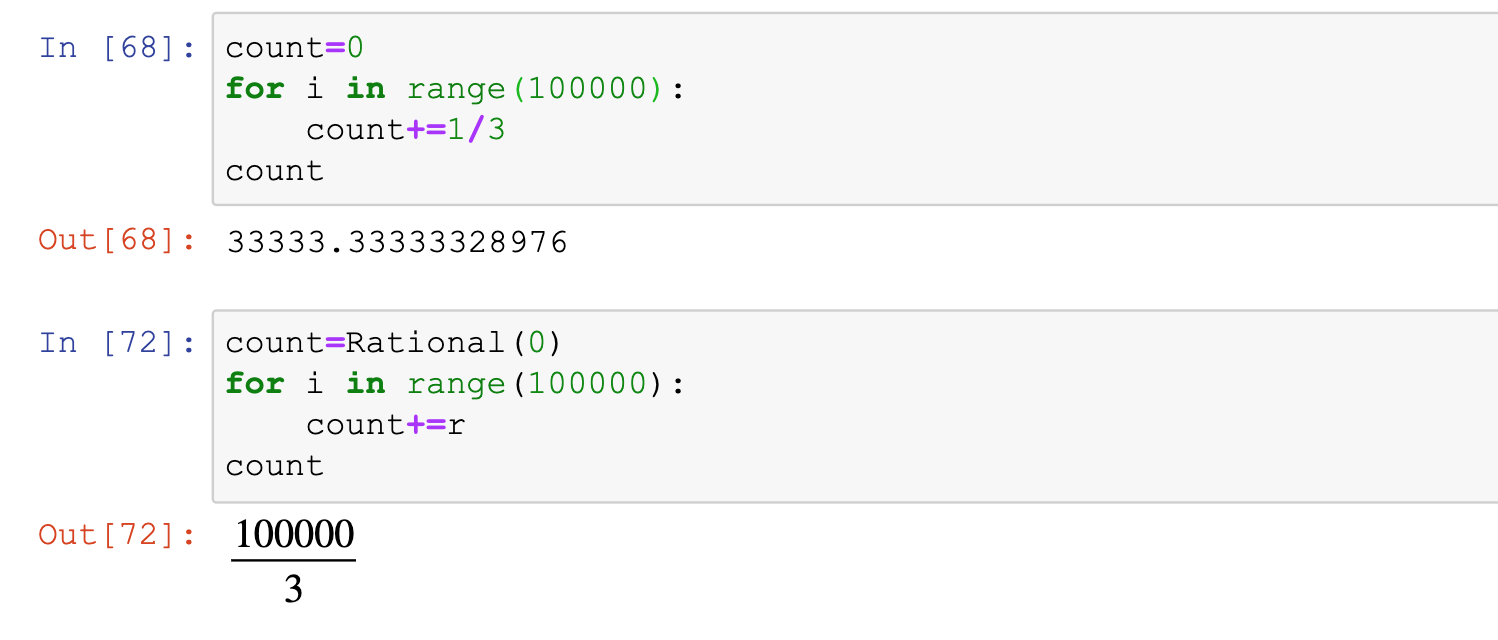
上面提到，在进行数值运算时，如果遇到除不尽的分数，则计算机会自动将其转化为多位小数，每次转换都会出现误差（精度丢失），如果这样的运算次数增多时，误差会逐渐拉大，为避免出现这个问题，故可以使用sympy使用符号表达式运算后，再计算出该表达式的值即可

#sympy中的Rational函数即用来表达有理数，而其中最为有用的是用来表达分数或分式
from sympy import Rational
from sympy.abc import *
r=Rational(1,3) #即表示1/3
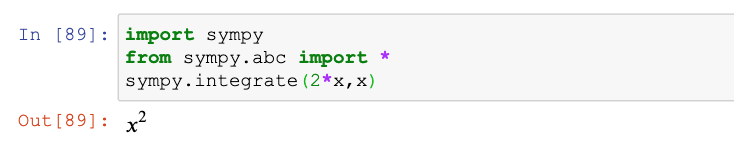
#如下计算结果，较为明显的表明，使用sympy的有理数表达方式，是极为精确的，因为计算过程均保留分数的形式
#最后只有到需要的时候，再将符号表达式转为数值即可

二、代数表达式相关运算

2.1 代数表达式

2.1.1 一元表达式

#代数表达式只由一个符号或者该符号经过有限次初等运算组成，在复习初中数学知识，主要明晰相关概念
import sympy
from sympy import symbols
x=symbols('x')
x+x**2+sin(x)  #一元代数表达式，LaTex展示效果如下

2.1.2 多元表达式

#代数表达式由多个符号或者多个符号经过有限次初等运算组成
import sympy
from sympy import symbols
x,y,z=symbols('x y z')
x+y**2+sin(z)  #多元代数表达式，LaTex展示效果如下

2.1.3 将字符串转换为符号表达式

#如果手上有一个字符串格式的表达式，或者该表达式是存储在数据库或由代码生成，此时想对该表达式使用sympy做进一步处理时，便需要将其转化为符号表达式
#此时，需要用到sympify函数，注意，不是simplify
import sympy
from sympy.abc import *
f='x+2*x+3'
f=sympy.sympify(f) #则会将字符串格式的表达式转变为符号表达式

2.2 代数表达式求值及值的替换

2.2.1 代数表达式求值

最终会将表达式转变为数值（整型、浮点型等等）

#对一元或多元表达式中的对应符号设置具体的数值，得出该表达式的值
#需要用到表达式的evalf函数，其中subs为substitute（代替）的简写，即哟经什么代替什么
#1、一元表达式求值
import sympy
x=symbols('x')
f=x+x**2
f.evalf(subs={x:2})#运算结果为6.0

#2、多元表达式求值
f=x+y**2+2*y
f.evalf(subs={x:2,y:3}) #运算结果为17

2.2.2 代数表达式值的替换

只是将表达式内某符号替换为指定的值或另外一个符号，并不会最终转变为数值

#此时需要使用subs函数
#1、替换一个符号
import sympy
from sympy.abc import *
f=x+2*x
f.subs(x,2) #最终输出的还是符号表达式
f.subs(x,a)

#2、替换多个符号
f=x+2*x+y+z
f.subs([(x,a),(y,b),(z,5)]) #将x替换为a，y替换为b，z替换为5
#或
f.subs({x:a,y:b,z:5}) #将x替换为a，y替换为b，z替换为5

2.2.3 转化为数值时指定精度

#在使用evalf函数将符号表达式转化为数值时，可指定转化后的数值精度
import sympy
from sympy.abc import *
f=sympy.sqrt(2)
f.evalf(6) #指定转化后的数值为6位精度

2.3 代数表达式运算

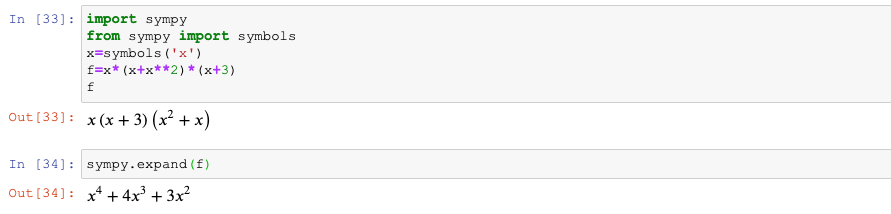
2.3.1 表达式展开为最小项表达式

#把任意一个代数表达式化成若干个最小项之和的形式，叫做表达式的展开
#该方法会尽力尝试消除表达式内的幂和乘法，主要还是可以降低对该表达式后续（积分等）处理的复杂度
#展开需要用到sympy的expand函数
import sympy
from sympy import symbols
x=symbols('x')
sympy.expand(x*(x+x**2)*(x+3))
#或
f=x*(x+x**2)*(x+3)
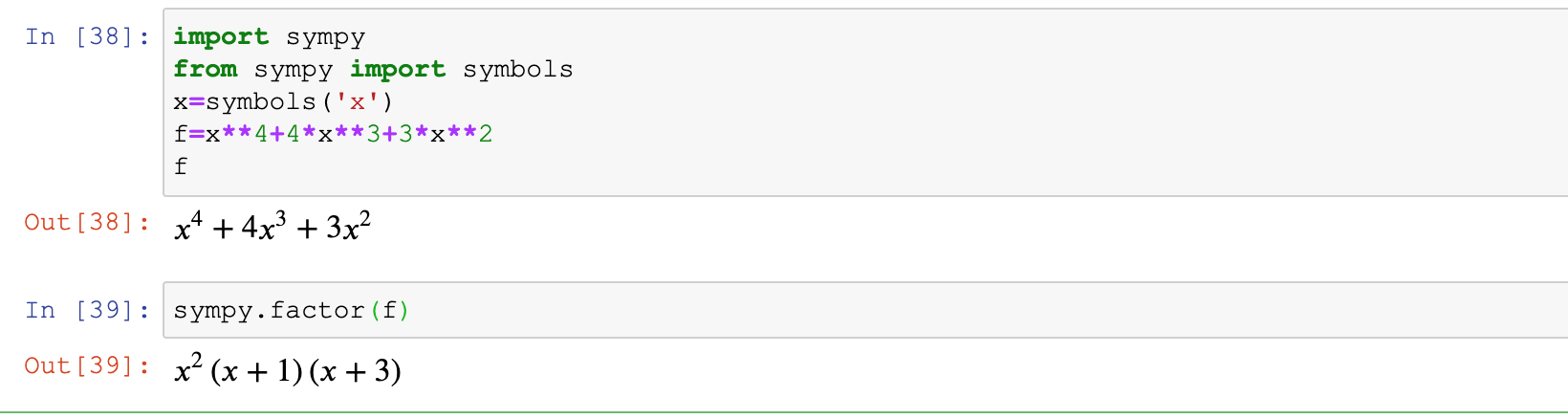
sympy.expand(f)

2.3.2 表达式因式分解

#因式分解，即把一个多项式在一个范围化为几个整式的积的形式
#因式分解，一般在求解方程的时候非常有用
import sympy
from sympy import symbols
x=symbols('x')
f=x**4+4*x**3+3*x**2
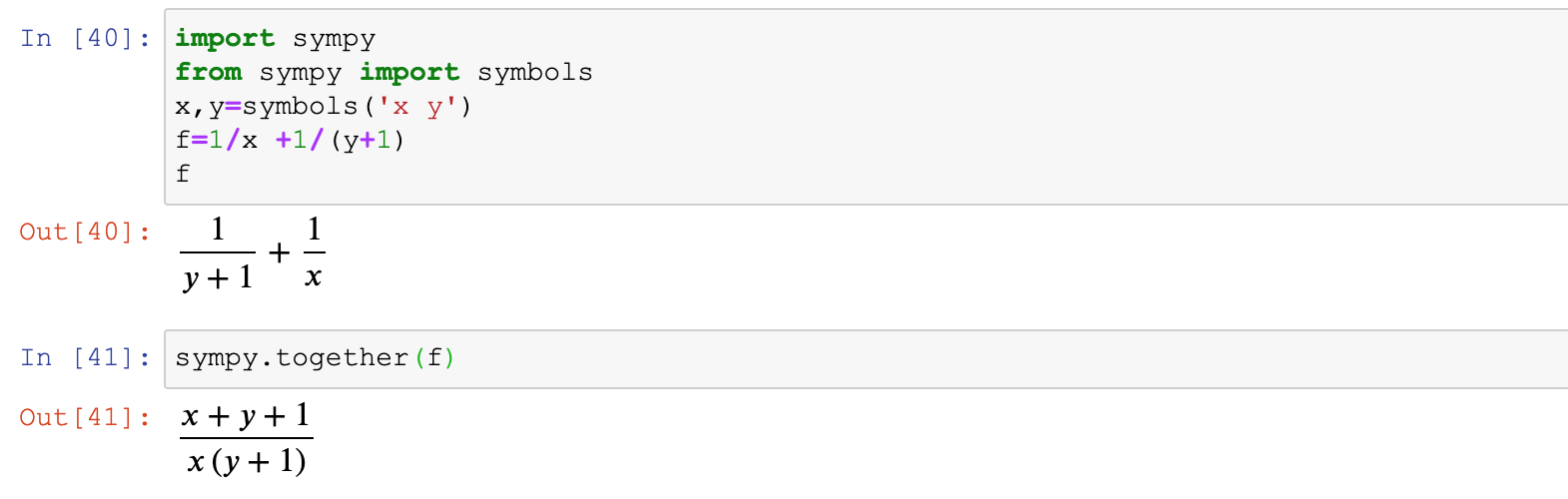
sympy.factor(f)

2.3.3 分式通分（合并）

#分式通分（合并），把几个异分母分数（式）化成与原来分数（式）相等的同分母的分数（式）
#通分一般用于比对两个分式的大小
import sympy
from sympy import symbols
x,y=symbols('x y')
f=1/x +1/(y+1)
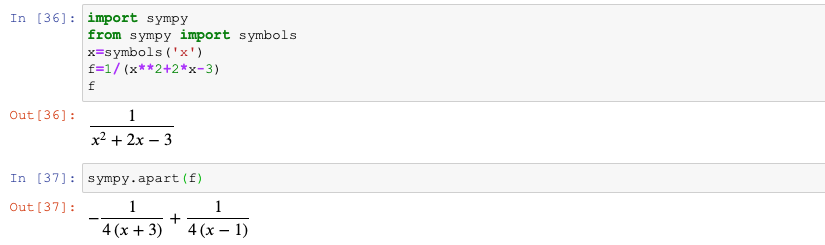
sympy.together(f)

2.3.4 分式分解（拆分）

#分式的分解（拆分）
#主要目的是将有理函数变为数个较简单的有理函数，或者说降低分式中多项式的复杂度，将一个复杂的分式分解成多个较为简单的分式，以降低对该分式进行其他运算（积分等）的复杂度
import sympy
from sympy import symbols
x=symbols('x')
f=1/(x**2+2*x-3)
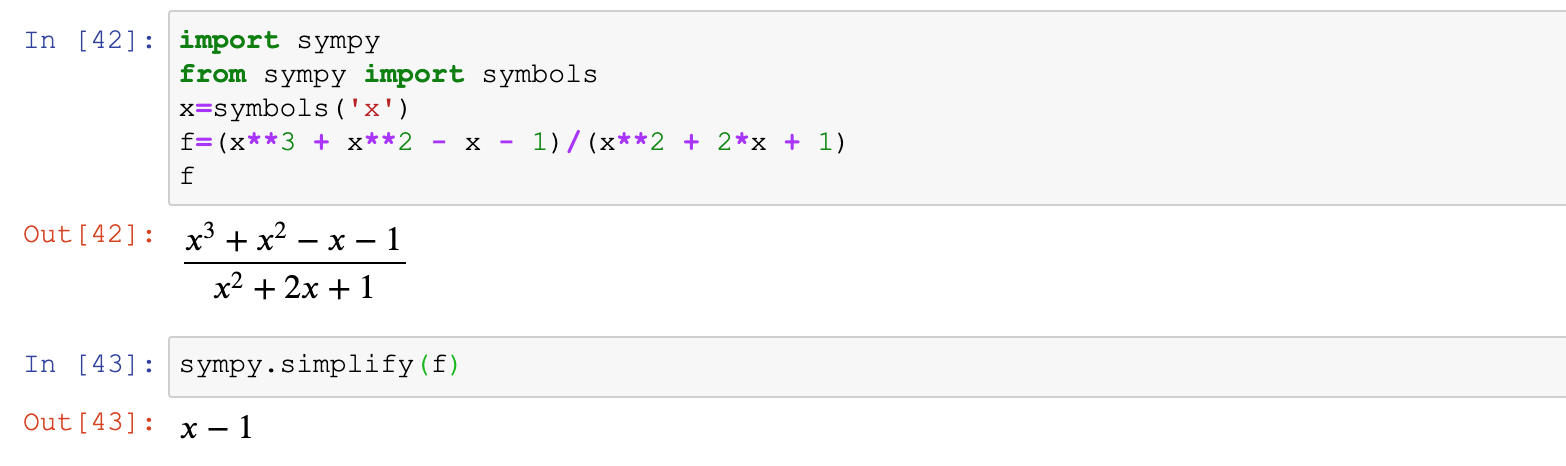
sympy.apart(f) #运算效果如下

2.3.5 表达式简化

#表达式化简是指将给定表达式转换为更为简单，也通常更短的一种形式。
#这一功能包括合并同类项、通分和约分。通过幂方程和三角函数，数学表达式简化还可以简化对数和指数表达式
#一般用于将表达式简化成最简形式，便于对表达式进行后续处理（求积分等）
import sympy
from sympy import symbols
x=symbols('x')
f=(x**3 + x**2 - x - 1)/(x**2 + 2*x + 1)
sympy.simplify(f)

2.3.6 表达式三角化简

#即将某符号表达式内的三角函数尽量化简，使得表达式内三角函数数量最小
from sympy import trigsimp,sin,cos
from sympy.abc import x,y
y = sin(x)/cos(x)
trigsimp(y) #结果为tan(x)

2.3.7 表达式比较

#比较两个符号表达式是否相等，不能使用==，需使用equals函数，函数返回布尔值
from sympy import sin,cos
from sympy.abc import *
f1=cos(x)**2 - sin(x)**2
f2=cos(2*x)
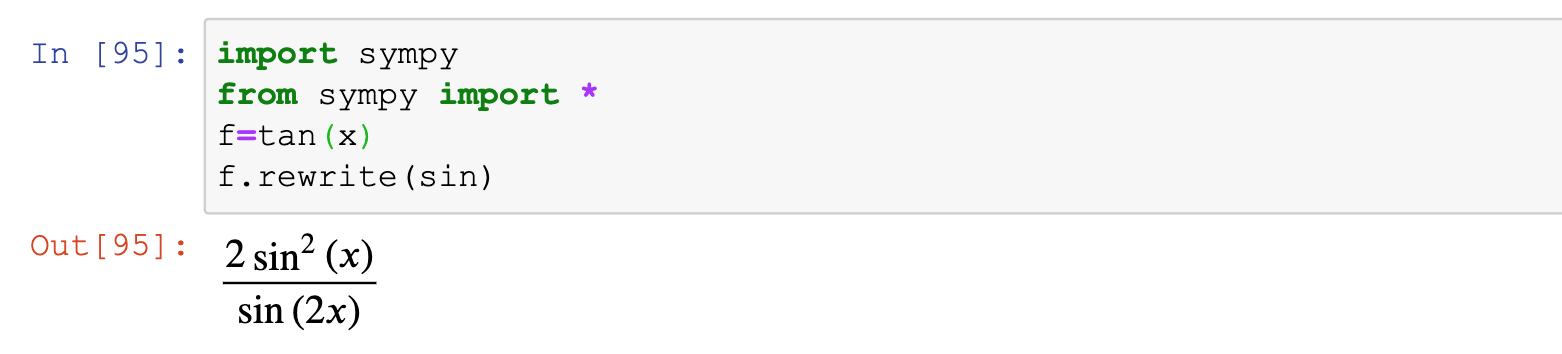
f1.equals(f2)  #结果为True

2.3.8 表达式重写

#重写，rewrite，即将某表达式从现有形式，写成指定的形式
import sympy
from sympy import *
f=tan(X)
f.rewrite(sin) #用sin函数表示tan函数

2.3.9 表达式泰勒展开

#如果想求某表达式的泰勒展开式，则使用series函数
import sympy
from sympy.abc import *
f=sympy.sin(x)
f.series(x,0,10) #其中0指在x的0位置展开，10指展开至最大10级
#如果不希望展示最后的误差项，则可以f.series(x,0,10).removeO()

三、方程式求解

3.1 概述

解代数方程式或方程组，是初等数学中比较重要的知识，一般包括求方程式、不等式、方程组、由多个不等式组成的方程组等，最终通过求解过程，获得某符号对应的值，或者多个符号之间的关系

方程式和方程组，一般用于抽象现实世界中多个变量之间的关系，并通过求解方程来探索各个变量之间的关系，但是前提一定要能先把各个未知变量之间的关系进行量化（包括组成方程或不等式）

#求解方程式或方程组，用到sympy的solve函数
sympy.solve(
    f,  #代数表达式（等式或者不等式），或由多个代数表达式组成的列表、元组等可迭代对象，表达式可由符号与代数运算符及函数组成（函数包括初等函数和超越函数，超越函数即三角函数等函数）
    *symbols, #需要求解的符号，可以是一个，或者由多个符号组成的列表
    **flags #设置返回的解的格式（set、dict）或其他特性，一般较为少用，会在下面详述
)

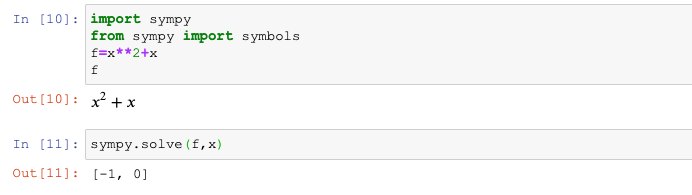
3.2 求一元方程式

3.2.1 一元等式

#求一元等式表达式，最为简单的方程式
import sympy
from sympy import symbols
f=x**2+x
sympy.solve(f,x) #运算过程如下,返回由x的解组成的列表

3.2.2 一元不等式

#求一元不等式
import sympy
from sympy import symbols
f=x**2+x<10
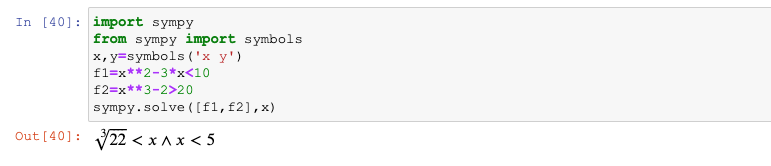
sympy.solve(f,x) #运算过程如下,返回一个不等式

3.3 求方程组

3.3.1 等式方程组

#求解由多个等式组成的方程组，一般需解出多个符号的值，如果需要求出确定的值，则需要保证未知符号个数与方程组内等式个数相等或小于方程组内等式个数
import sympy
from sympy import symbols
x,y=symbols('x y')
f1=x**2+y-3
f2=x+y-2
ssympy.solve([f1,f2],[x,y]) 
#如果每个待求解符号解都只有一个，默认会返回一个字典，字典以待求解符号作为键，以对应的解作为值
#如果每个待求解符号解有多个，会返回一个列表，列表内由元组组成，每个元组内含对应多个解

3.3.2 不等式方程组

#求解不等式方程组，即由多个不等式组成的方程式组
#实际情况中，一般是希望找出待求解符号，满足方程式组的取值范围，且一般也只能求出一个符号的取值范围
import sympy
from sympy import symbols
x,y=symbols('x y')
f1=x**2-3*x<10
f2=x**3-2>20
sympy.solve([f1,f2],x)

3.4 求解符号组合

#上面的例子，一般是直接求解符号本身的取值范围或值
#也可求解由符号组成的对象本身，比如(x+3)
import sympy
from sympy.abc import *
eqs=(x*y + 3*y + sympy.sqrt(3), x + 4 + y)
sympy.solve(eqs, [y*x, x])#会返回y*x以及x的解

3.5 其他参数解释

参数	说明	示意
dict	布尔，默认False，当为True时，则以列表形式返回各符号的解，列表内每个元素即字典格式，字典键值分别为符号与其解，如果有多个解，则列表有多个字典元素	[{xy: -3y – sqrt(3), x: -y – 4}]
set	布尔，默认False，当为True时，则以列表形式返回待求解符号，以集合格式返回符号对应的解	([x, xy], {(-y – 4, -3y – sqrt(3))})

四、求极限

4.1 极限概述

#极限是研究函数特性的重要思想和工具（比如收敛等性质），也是微积分的基础
#极限是表征现实世界中变化状态，其内涵指的是无限接近而永远达不到，在函数极限的概念中，即函数中某一变量的值无限接近于指定的值而永远达不到，此时该函数对应的值，就叫函数在该点的极限值
#极限涉及到函数的连续性、收敛性等重要特性，函数在其变量的某个点是否连续，一个很重要的特征便是极限存在且等于函数值，而极限存在则要求该函数在该点的左极限和右极限相等
sympy.limi(
    f,#函数或代数表达式
    x,#变量
    a,#指定变量的趋向值
    dir='' #趋向方式，dir='-'即从左侧趋近，dir='+'即从右侧趋近，dir='+-'即从双侧趋近
)

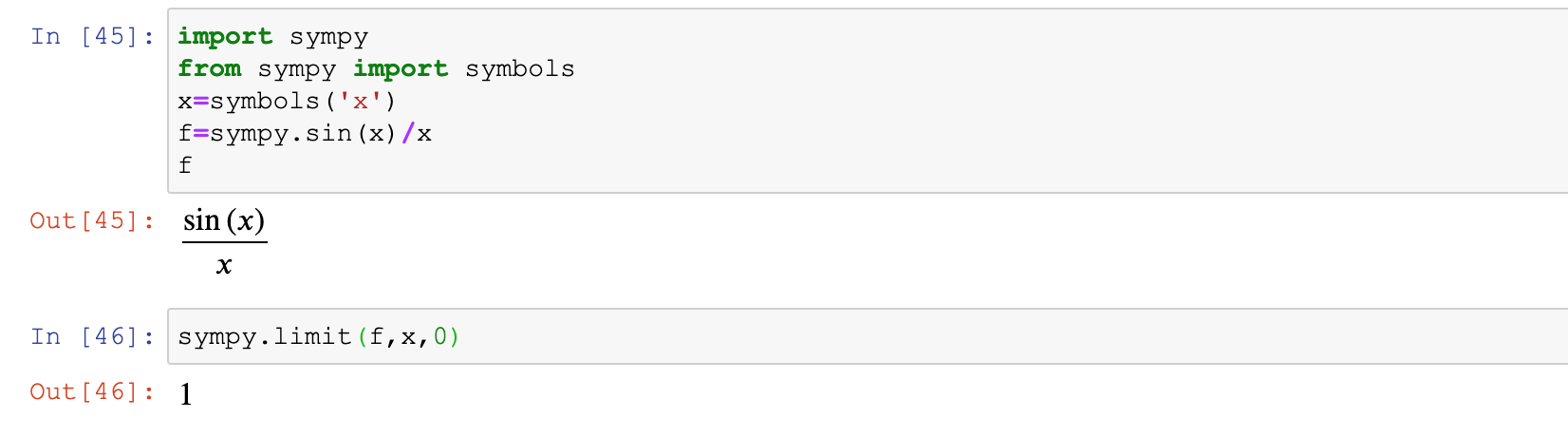
import sympy
from sympy import symbols
x=symbols('x')
f=sin(x)/x
sympy.limit(f,x,0) #f为函数，x为变量，0为趋向值，即在变量指定点的极限

4.2 左极限

#求函数或表达式极限的时候，分为左极限和右极限
#左极限，指从左边无限靠近指定点，所得到的函数或表达式的极限值
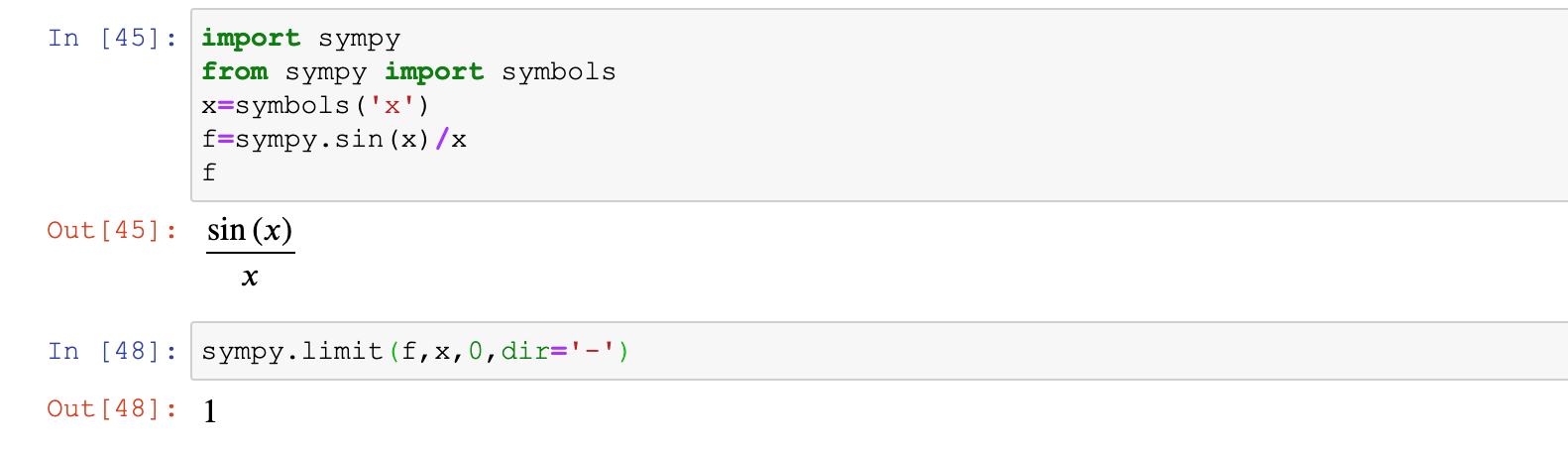
import sympy
from sympy import symbols
x=symbols('x')
f=sin(x)/x
sympy.limit(f,x,0,dir='-') #f为函数，x为变量，0为趋向值，即在变量指定点的极限，dir定义从哪个方向趋近，'-'代表左极限

4.3 右极限

#求函数或表达式极限的时候，分为左极限和右极限
#右极限，指从右边无限靠近指定点，所得到的函数或表达式的极限值
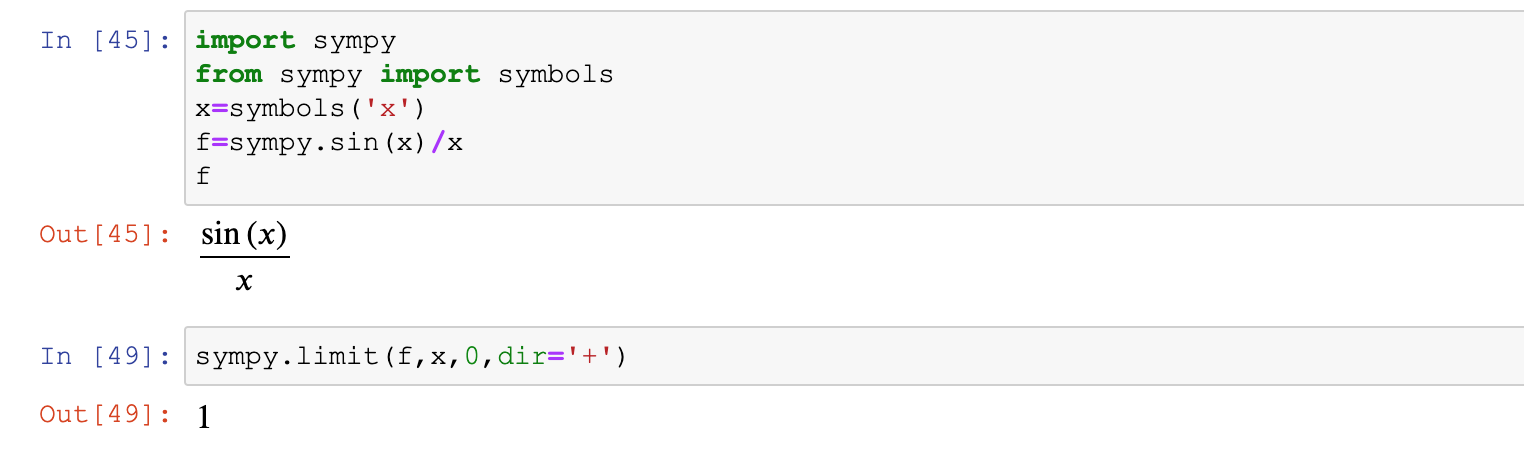
import sympy
from sympy import symbols
x=symbols('x')
f=sin(x)/x
sympy.limit(f,x,0,dir='+') #f为函数，x为变量，0为趋向值，即在变量指定点的极限，dir定义从哪个方向趋近，'+'代表右极限

五、求导

5.1 概述

#导数的定义是，当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。
#在一个函数存在导数时，称这个函数可导或者可微分。其实微积分和微积分计算的重要基础
#寻找已知的函数在某点的导数或其导函数的过程称为求导，或者叫求原函数的微分。实质上，求导就是一个求极限的过程，已知导函数倒过来求原函数，即不定积分，积分相关概念会在下面介绍
#求导需要用到sympy.diff函数
sympy.diff(
    f,#代数或符号表达式，即需要求导的表达式，可以是一元，也可以是多元，只能传入一个表达式
    symbols,#如果是只有一个符号，或求偏导，则可直接传入指定符号；如果求高阶导，则可以元组(x,3)形式传入，如果需要求全导，则可传入多个元组，并分别指定对应的高阶导值
)

#下面是求一个基础的一元表达式的一阶导
import sympy
from sympy import symbols
from sympy.abc import *
sympy.diff(x**3,x)

5.2 偏导（偏微分）与全导

#如果需要求导的表达式是多元表达式，则可求某指定符号的偏导，也可求全部符号的全导
#1、求偏导
import sympy
from sympy import symbols
from sympy.abc import *
sympy.diff(x**2*y**3,x) #运算过程如下左图所示

#2、求全导
import sympy
from sympy import symbols
from sympy.abc import *
sympy.diff(x**2*y**3,x,y) #运算过程如下右图所示

5.3 高阶导

#求某表达式的2阶及以上阶的导数或导函数
#1、高阶偏导
import sympy
from sympy import symbols
from sympy.abc import *
sympy.diff(x**2*y**3,x,2)  #运算结果如下左图
#或者sympy.diff(x**2*y**3,(x,2))

#2、高阶全导
import sympy
from sympy import symbols
from sympy.abc import *
sympy.diff(x**2*y**3,x,2,y,2) #运算结构如下右图所示
#或者sympy.diff(x**2*y**3,(x,2),(y,2))

六、求积分

6.1 概述

#求积分，尤其是求定积分（简称求积分），是高等数学中微积分非常重要的基础知识和运算
#求积分时要用到integrate函数，该函数简述如下
sympy.integrate(
    f, #主要是传入待求积分的表达式，只能传入一个，可传一元表达式，也可传多元表达式
    var,#主要传入待积分的符号，比如x等，有以下三种形式：
    #1、只传入符号，则此时求的是不定积分，即该表达式的原函数
    #2、传入一个元组，但只指定了符号的积分下限,比如(x,a)，则此时求的也是不定积分，不过会将结果中的x用a替换
    #3、传入一个元组，同时指定符号的积分上下限，比如(x,a,b)，则此时求的是定积分，即一个值
)

6.2 定积分

#即求某个一元表达式，符号在指定取值区间范围内的积分值
import sympy
from sympy.abc import *
sympy.integrate(2*x,(x,1,3)) #求2x在1到3区间范围内的定积分值

定积分表达式： $\int_{1}^{3}2xdx$ 运算过程如下：

6.3 不定积分

#即求某个一元表达式或函数的原函数
import sympy
from sympy.abc import *
sympy.integrate(2*x,x) #求2x的不定积分，即原函数

不定积分表达式： $\int 2xdx$ 运算过程如下：

6.4 多重积分

6.4.1 多重定积分

#当传入的表达式或函数是多元时（包含多个符号），则求该表达式的积分就叫多重积分，或者叫多元积分
#计算多重积分时，var变量，传入多个元组，每个元组指定对应符号及取值区间范围
##传入的元组数量不限
import sympy
from sympy.abc import *
sympy.integrate(2*x+y,(x,2,4),(y,5,8))

多重定积分，积分区域为： $D=\left \{ (x,y) |a\leq x\leq b,c\leq y\leq d\right \}$ 定积分公式为： $\int_{c}^{d}dy\int_{a}^{b}(2x+y)dx$ 运算过程如下：

6.4.2 多重不定积分

#计算多重积分时，var变量，只传入了符号，则此时计算的是多重不定积分，即全导的逆计算过程
#传入的符号数量不限，传入2个叫2重积分，n个即n重积分
import sympy
from sympy.abc import *
sympy.integrate(2*x+y,x,y)

多重不定积分公式： $\int \int (2x+y)dxdy$ 运算过程如下：

6.5 其他参数介绍

参数	说明	示意
meijerg	布尔，默认False，枚举True、False、None，分别表示只使用G函数、永远不使用G函数或用所有可用的函数求积分，默认None	meijerg=True
conds	枚举值：’piecewise’, ‘separate’ 、 ‘none’，暂时未用到，待用到时再补充
risch	枚举值：True、False、None，暂时未用到，待用到时再补充
heurisch	枚举值：True、False、None，暂时未用到，待用到时再补充
manual	枚举值：True、False、None，暂时未用到，待用到时再补充

七、求解微分方程

7.1 概述

#解微分方程，是高等数学以及实际应用中，很重要的课题，求解的过程，其实就是在求原函数的过程，微分方程一般体现的是几个变量之间实际变化的规律，然后依据该变化规律，反向求出几个变量之间的静态规律（也即求出某个指定函数，该函数可能包含一个或多个变量）
#比如知道某汽车行驶的速度变化规律，求汽车行驶路程与时间之间的关系
#比如知道某河流流量随河道宽度的变化关系，也知道河流流量随河道高度的变化关系，求河流流量与河道宽度及河道高度的关系

#微分方程的定义：凡含有参数,未知函数和未知函数导数 (或微分) 的方程
#常微分方程：未知函数是一元函数的微分方程称作常微分方程
#偏微分方程：未知函数是多元函数的微分方程称作偏微分方程，其中方程内可能含有偏微分（偏导）
#微分方程的阶：微分方程中出现的未知函数最高阶导数的阶数,称为微分方程的阶

#求解偏微分方程，是在应对复杂实际数学问题时，最常用到的，但也是相对比较难求解的，目前看来，sympy并没有提供求解偏微分方程的方法

#求解微分方程，需要使用dsolve函数
sympy.dsolve(
    eq, #待解的微分方程，可传入一个或多个，如果是多个，则用
    func=None, #待求解的函数（原函数），一般情况需不需要传入，会自动识别出来
    hint='default',#设置求解微分方程的方法，一般无需特别指明，会尝试使用所有可用的方法
    simplify=True, #将求解结果进行尽量简化，一般采用默认值即可
    ics=None,#传入边界条件，求解特解，即initial_condition_set，类似：{f(a): b, f(x).diff(x).subs(x, c):d} 的形式
    xi=None,#暂未接触到
    eta=None,#暂未接触到
    x0=0, #指定如果微分方程的解为级数序列时，在指定哪个位置进行展开
    n=6,#指定如果微分方程的解为级数序列时，其最高的幂级数
)

7.2 求解常微分方程

#求解常微分方程，求通解
#一个实际的例子，比如知道一个车辆的速度随时间的变化规律，设路程为s，速度为v，时间为t，而速度的变化规律为v=2t-s，求路程与时间的关系
#则对应的微分方程为s'=2*t-s
#1、求通解
import sympy
from sympy import symbols,Function,Eq
from sympy.abc import *
s=symbols('s',cls=Function)
eq=Eq(s(t).diff(t),2*t-s(t))
sympy.dsolve(eq,s(t)) #求出针对以上问题的通解

#2、求满足特定条件的特解
#针对以上问题，在t=0时，s=0，所以有s(0)=0，然后基于该条件，求出其中的常量具体值即可
#此时需将边界条件传入ics参数
eq=Eq(s(t).diff(t),2*t-s(t))
solution=sympy.dsolve(eq,s(t),ics={s(0):0})

7.3 求解常微分方程组

#自变量只有1个，因变量有多个（即待求解的因变量函数有多个），且每个方程均由这些待求解的函数及其导函数组成，且不能出现偏导，一旦出现偏导，肯定就是偏微分方程，而sympy无法求解偏微分方程
from sympy import Function,symbols,Eq,exp,dsolve
t=symbols('t')
x,y=symbols('x y',cls=Function)

eq1=Eq(x(t).diff(t,1),3*x(t)-2*y(t))
eq2=Eq(y(t).diff(t,1),2*x(t)-y(t))
dsolve((eq1,eq2),[x(t),y(t)]) #运算结果如下

常微分方程组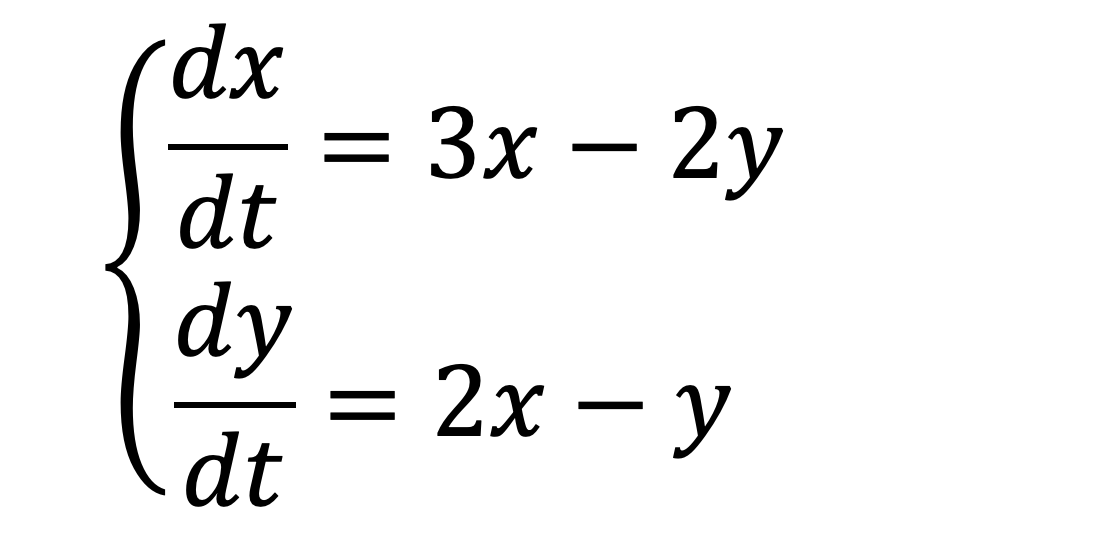：求解过程如下：

八、绘图

可以直接传入代数表达式便可以直接绘制出该表达式对应函数图，应该是sympy比较有意思的地方，因为可以帮我们快速的、可视化的观察某些函数的特点。

sympy的绘图函数也是plot，并且有一些与matplotlib相类似的参数，比如设置x和y轴的值范围、设置title等等。

8.1 概述

#sympy.plot函数使用简介
sympy.plot(
    *args, #指定需要绘图的一元表达式或函数，可以传入多个，传入多个则代表一次性绘制多个表达式或函数的图
    show=True, #指定绘图后是否展示，默认展示，一般无需进行设置
    **kwargs #指定变量的取值区间，是一个三元素元组，比如(x,-6,6)，即指定x在-6到6区间内取值并绘图
)
#函数范围一个sympy的Plot对象，类似matplotlib的Figure对象，可以使用该对象对绘图结果进行保存，或者进一步设置该图其他的属性

8.2 绘单图

#使用sympy.plot函数给代数表达式绘图
import sympy
from sympy import symbols,sin,plot
x=symbols('x')
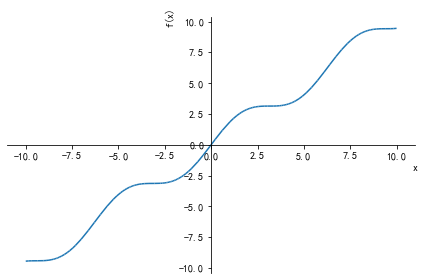
f=x+sin(x)
plot(f)#绘图结果如下

8.3 绘多图

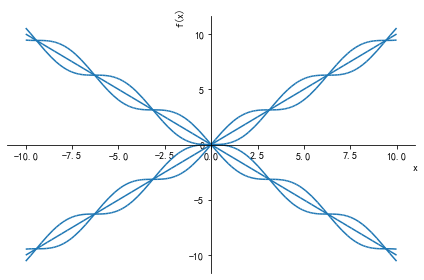
#使用sympy.plot函数给多个代数表达式绘图，且绘制到一张图内
import sympy
from sympy import symbols,sin,plot
x=symbols('x')
f1=x+sympy.sin(x) 
f2=x
f3=x-sympy.sin(x)
f4=-x+sympy.sin(x) 
f5=-x
f6=-x-sympy.sin(x)
plot(f1,f2,f3,f4,f5,f6)#绘图结果如下

8.4 指定绘图区间范围

#1、为一个或多个绘图，指定统一的绘图区间范围
import sympy
from sympy import symbols
x=symbols('x')
f1=x+sympy.sin(x)
f2=x
sympy.plot(f1,f2,(x,-5,5)) #绘图结果如下左图所示

#2、为多个绘图，分别指定绘图区间范围
f1=x+sympy.sin(x)
f2=-x+sympy.sin(x)
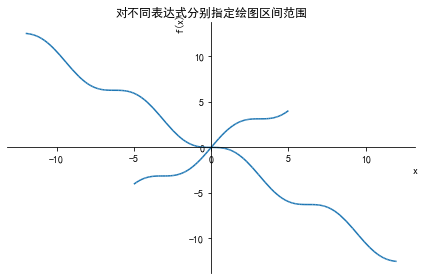
sympy.plot((f1,(x,-5,5)),(f2,(x,-12,12)),title='对不同表达式分别指定绘图区间范围') #绘图结果如下右图所示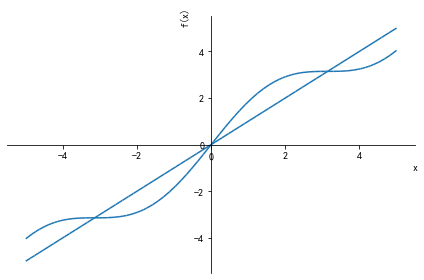

8.5 其他绘图函数参数

参数	说明	示意
title	str，设置图表标题，字符串格式	title=’我是图表标题’
label	str，表达式在图表内的标签名，只有与legend=True配合时才有效，且只能设置一个，一般不需要使用	label=’sin(x)’
xlabel	str，x轴标签	xlabel=’我是x轴标签’
ylabel	str，y轴标签	ylabel=’我是y轴标签’
xscale	枚举，’linear’ or ‘log’，设置x轴的坐标尺寸，是线性的还是对数型	xscale=’log’
yscale	枚举，’linear’ or ‘log’，设置y轴的坐标尺寸，是线性的还是对数型	yscale=’log’
xlim	元组，设置x轴坐标取值区间范围，默认是(-10,10)	xlim=(-20,10)
ylim	元组，设置y轴坐标取值区间范围，默认是(-10,10)	ylim=(-20,10)
size	元组，设置图表整体的大小，单位英尺	size=(10,8)
axis_center	元组，设置图表的坐标轴中心，默认是(0,0)，即默认坐标轴原点为中心	axis_center=(2,2)

今天的文章python符号用法_python绘制图形分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/74721.html