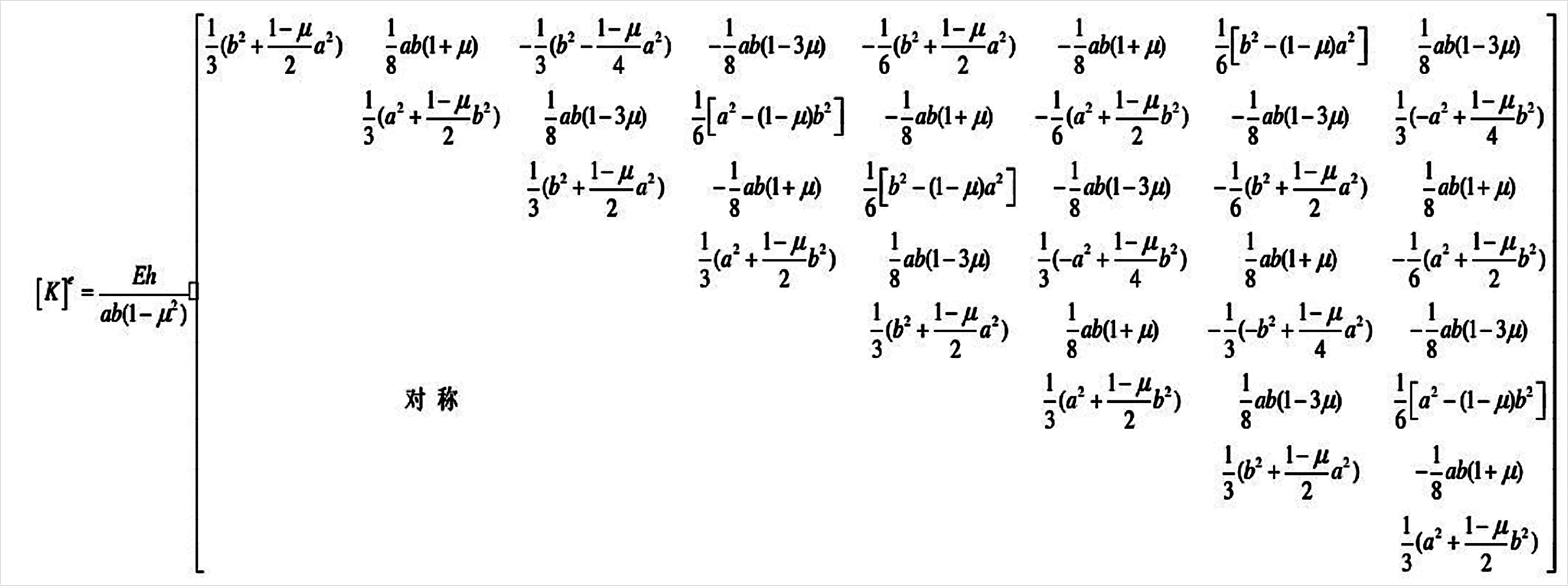1. 编程号首页

拓扑优化99行代码_画拓扑图的软件免费版

编程小号 • • 未分类

拓扑优化99行代码_画拓扑图的软件免费版:）ClickHereForMoreDetails.最近学习Sigmund的99行Matlab拓扑优化程序，参考了其他大神们的注释，作为初学者还有不少看不懂的地方，结合论文学习又补充整理了一遍

 博客搬家到自己搭建的 主页 啦q(≧▽≦q)，大家快来逛逛鸭！

 

拓扑优化99行代码_画拓扑图的软件免费版

 The Corresponding Files (Click to Save):

  • Code:            top.m
  • References:   A 99 line topology optimization code written in MATLAB

The Related Artical (Click in):

  • >TopOpt | 99行拓扑优化程序完全注释
  • TopOpt | 针对99行改进的88行拓扑优化程序完全注释
  • TopOpt | 88行拓展的82行拓扑优化程序完全注释. PDE
  • TopOpt | 88行拓展的71行拓扑优化程序完全注释. CONV2

The program can be promoted by line:

top(30,10,0.5,3.0,1.5)

代码注释

以前学了点皮毛就直接用商业软件搬砖了，总觉得有点心虚，所以入门第一步，拜读了Sigmund的99行Matlab拓扑优化程序，参考了其他大神们的注释，作为初学者还有不少看不懂的地方，我自己又补充整理了一遍。我是零基础小白，所以代码前面先交代了一些理论背景，我自己能看懂相信所有人都能看懂，哈哈哈。

%%%%%%%%  A 99 LINE TOPOLOGY OPTIMIZATION CODE BY OLE SIGMUND, JANUARY 2000  %%%%%%%%
%%%%%%%%  COMMENTED - OUT 1.0 BY HAOTIAN_W,                       JULY 2020  %%%%%%%%
function top(nelx,nely,volfrac,penal,rmin)
% ===================================================================================
% nelx    : 水平方向上的离散单元数;
% nely    : 竖直方向上的离散单元数;
%
% volfrac : 容积率，材料体积与设计域体积之比，对应的工程问题就是"将结构减重到百分之多少";
%
% penal   : 惩罚因子，SIMP方法是在0-1离散模型中引入连续变量x、系数p及中间密度单元，从而将离
%           散型优化问题转换成连续型优化问题，并且令0≤x≤1，p为惩罚因子，通过设定p>1对中间密
%           度单元进行有限度的惩罚，尽量减少中间密度单元数目，使单元密度尽可能趋于0或1;
% 
%           合理选择惩罚因子的取值，可以消除多孔材料，从而得到理想的拓扑优化结果:
%               当penal<=2时     存在大量多孔材料，计算结果没有可制造性;
%               当penal>=3.5时   最终拓扑结果没有大的改变;
%               当penal>=4时     结构总体柔度的变化非常缓慢，迭代步数增加，计算时间延长;
%            
% rmin    : 敏度过滤半径，防止出现棋盘格现象;
% ===================================================================================
% 结构优化的数学模型常用名词:
%   1) 设计变量   在设计中可调整的、变化的基本参数，本算例是单元密度;
%   2) 目标函数   设计变量的函数，优化设计的目标，本算例是柔度最小;
%   3) 约束条件   几何、应力、位移等，难点在建立约束方程，本算例是几何体积约束;
%   4) 终止准则   结束迭代的条件，本算例是目标函数变化量<=0.010;
%   5) 载荷工况   定义结构所有可能的受力情况，本算例是单一载荷;
% ===================================================================================
% 基于SIMP理论的优化准则法迭代分析流程:
%   1) 定义设计域，选择合适的设计变量、目标函数以及约束函数等其他边界条件;
%   2) 结构离散为有限元网格，计算优化前的单元刚度矩阵;
%   3) 初始化单元设计变量，即给定设计域内的每个单元一个初始单元相对密度;
%   4) 计算各离散单元的材料特性参数，计算单元刚度矩阵，组装结构总刚度矩阵，计算结点位移;
%   5) 计算总体结构的柔度值及其敏度值，求解拉格朗日乘子;
%   6) 用优化准则方法进行设计变量更新;
%   7) 检查结果的收敛性，如未收敛则转4)，循环迭代，如收敛则转8);
%   8) 输出目标函数值及设计变量值，结束计算。
% ===================================================================================

% x是设计变量，给设计域内的每个单元一个初始相对密度，值为volfrac
x(1:nely,1:nelx) = volfrac; 

% loop储存迭代次数
loop = 0; 

% change储存每次迭代之后目标函数的改变值，用以判断是否收敛
change = 1.;

% 当目标函数改变量<=0.01时说明收敛，结束迭代
while change > 0.01
    loop = loop + 1; 
    
    % 将前一次的设计变量赋值给xold，x用来储存这一次的结果，之后还要比较它们以判断是否收敛
    xold = x;  

    % 每次迭代都进行一次有限元分析，计算结点位移，并储存在全局位移数组U中
    [U] = FE(nelx,nely,x,penal);   
    
    % 计算单元刚度矩阵
    [KE] = lk;
    
    % c是用来储存目标函数的变量
    c = 0.;
    
    % 遍历设计域矩阵元素，从左上角第一个元素开始，一列一列
    for ely = 1:nely
        for elx = 1:nelx
            
            % 节点位移储存在U中，如果想获得节点位移必须先知道节点编号，进行索引;
            % 节点编号可以根据当前单元在设计域中的位置算出;
            % n1是左上角节点编号，n2是右上角节点编号;
            n1 = (nely+1)*(elx-1)+ely; 
            n2 = (nely+1)*elx+ely;
           
            % 局部位移数组Ue储存4个节点共8个自由度位移，每个节点分别有x、y两个自由度; 
            % 因为是矩形单元，所以根据n1、n2两个节点的编号可以推演出单元所有节点的自由度编号;
            % 顺序是：[左上x；左上y；右上x；右上y；右下x；右下y；左下x；左下y];
            % 只适用于矩形单元划分网格;
            Ue = U([2*n1-1;2*n1; 2*n2-1;2*n2; 2*n2+1;2*n2+2; 2*n1+1;2*n1+2],1);
         
            % SIMP模型，将设计变量x从离散型变成指函数型，指数就是惩罚因子：x(ely,elx)^penal
            % 计算总体结构的柔度值，这里目标函数是柔度最小，参见论文中公式（1）
            c = c + x(ely,elx)^penal*Ue'*KE*Ue;
            
            % 计算总体结构的敏度值，实际上dc就是c对Xe的梯度，参见论文中公式（4）
            dc(ely,elx) = -penal*x(ely,elx)^(penal-1)*Ue'*KE*Ue;
        end
    end
    
    % 无关网格敏度过滤
    [dc] = check(nelx,nely,rmin,x,dc); 
    
    % 采用优化准则法（OC）求解当前模型，得出满足体积约束的结果，更新设计变量
    [x] = OC(nelx,nely,x,volfrac,dc);
    
    % 更新目标函数改变值
    change = max(max(abs(x-xold)));
    
    % 打印迭代信息: It.迭代次数，Obj.目标函数，Vol.材料体积比，ch.迭代改变量
    disp([' It.: ' sprintf('%4i',loop) ' Obj.: ' sprintf('%10.4f',c) ...
       ' Vol.: ' sprintf('%6.3f',sum(sum(x))/(nelx*nely)) ...
        ' ch.: ' sprintf('%6.3f',change )])
    
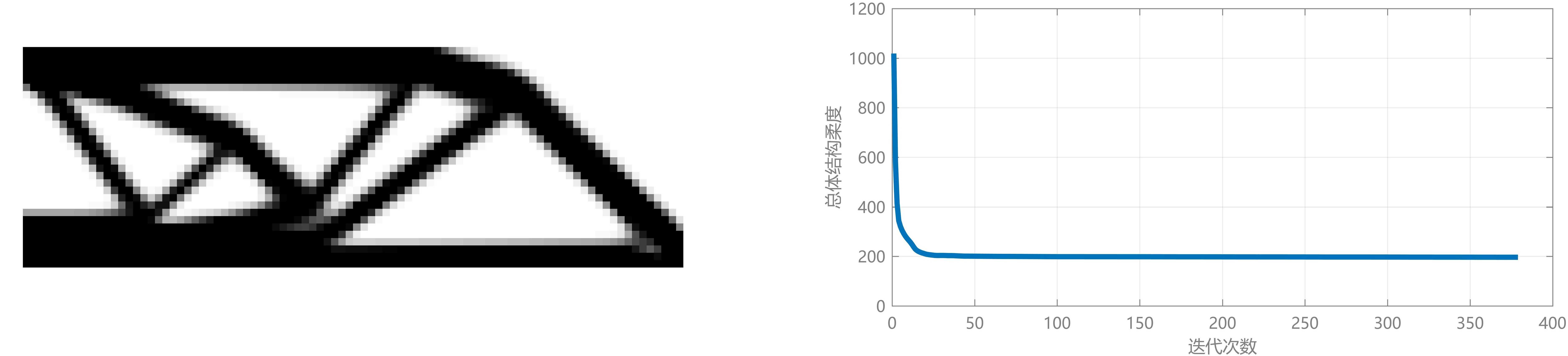
    % 当前迭代结果图形显示
    colormap(gray); imagesc(-x); axis equal; axis tight; axis off;pause(1e-6);
end


% 采用优化准则法（OC）迭代子程序 -------------------------------------------------------
% 数学模型主要求解算法有：优化准则法(OC)、序列线性规划法(SLP)、移动渐进线法(MMA); 
% OC适用于单约束优化问题求解，比如这里的"体积约束下的柔度最小化"问题，当求解复杂的多约束拓扑
% 优化问题时，采用SLP和MMA通常更方便;
% 参见论文中公式（2）（3）
function [xnew] = OC(nelx,nely,x,volfrac,dc)
% Input：  水平单元数nelx, 竖直单元数nely, 设计变量x, 材料体积比volfrac, 目标函数灵敏度dc;
% Output： 更新后的设计变量xnew;

% 定义一个取值区间，二分法，得到满足体积约束的拉格朗日算子
l1 = 0; l2 = 100000;

% 正向最大位移
move = 0.2;

while (l2-l1 > 1e-4)
    
    % 二分法，取区间中点
    lmid = 0.5*(l2+l1);
  
    % 参见论文中的公式（2）
    % sqrt(-dc./lmid)对应公式中Be^eta（eta=1/2），eta阻尼系数是为了确保计算的收敛性
    xnew = max(0.001,max(x-move,min(1.,min(x+move,x.*sqrt(-dc./lmid)))));
    
    % sum(sum(xnew))是更新后的材料体积, volfrac*nelx*nely是优化目标，用它们的差值判断是否收敛
    % sum()可以去看看help，注意一下行、列问题，不看也行，反正知道sum(sum())是所有元素求和就行
    if sum(sum(xnew)) - volfrac*nelx*nely > 0
        l1 = lmid;
    else
        l2 = lmid;
    end
end


% 无关网格敏度过滤子程序 --------------------------------------------------------------
% 参见论文中公式（5）（6）
function [dcn] = check(nelx,nely,rmin,x,dc)
% Input：  水平单元数nelx, 竖直单元数nely, 敏度过滤半径rmin, 设计变量x, 总体结构敏度dc;
% Output： 过滤后的目标函数敏度dcn;

% dcn清零，用来保存更新的目标函数灵敏度
dcn = zeros(nely,nelx);

for i = 1:nelx   
    for j = 1:nely
        sum=0.0; 
        
        % 在过滤半径定义的范围内遍历
        for k = max(i-floor(rmin),1):min(i+floor(rmin),nelx)
            for l = max(j-floor(rmin),1):min(j+floor(rmin),nely)
                
                % 参见论文中公式（6）,fac即公式中卷积算子Hf
                % qrt((i-k)^2+(j-l)^2) 是计算此单元与相邻单元的距离，即公式中dist(e,f)
                fac = rmin-sqrt((i-k)^2+(j-l)^2);
                sum = sum+max(0,fac);
                
                % 参见论文中公式（5）
                dcn(j,i) = dcn(j,i) + max(0,fac)*x(l,k)*dc(l,k);
            end
        end
        dcn(j,i) = dcn(j,i)/(x(j,i)*sum);
    end
end


% 有限元求解子程序 --------------------------------------------------------------------
function [U] = FE(nelx,nely,x,penal)
% Input：  水平单元数nelx, 竖直单元数nely, 设计变量x, 惩罚因子penal;
% Output： 全局节点位移U;

% 计算单元刚度矩阵
[KE] = lk; 

% 总体刚度矩阵的稀疏矩阵
K = sparse(2*(nelx+1)*(nely+1), 2*(nelx+1)*(nely+1));

% 力矩阵的稀疏矩阵
F = sparse(2*(nely+1)*(nelx+1),1); 

% U清零，用来保存更新的全局节点位移
U = zeros(2*(nely+1)*(nelx+1),1);

for elx = 1:nelx
    for ely = 1:nely
        
        % 计算单元左上角、右上角节点编号
        n1 = (nely+1)*(elx-1)+ely; 
        n2 = (nely+1)* elx   +ely;
        
        % 同上主程序，计算单元4个节点8个自由度
        edof = [2*n1-1; 2*n1; 2*n2-1; 2*n2; 2*n2+1; 2*n2+2; 2*n1+1; 2*n1+2];
        
        % 将单元刚度矩阵KE 组装成 总体刚度矩阵K
        K(edof,edof) = K(edof,edof) + x(ely,elx)^penal*KE;
    end
end

% 施加载荷，本算例应用了一个在左上角的垂直单元力
F(2,1) = -1;

% 施加约束，消除线性方程中的固定自由度来实现支承结构，本算例左边第一列和右下角固定
fixeddofs = union([1:2:2*(nely+1)],[2*(nelx+1)*(nely+1)]);

% 剩下的不加约束的节点自由度，setdiff()从..中除去..
alldofs   = [1:2*(nely+1)*(nelx+1)];
freedofs  = setdiff(alldofs,fixeddofs);

% 求解线性方程组，得到各节点自由度的位移值储存在U中
U(freedofs,:) = K(freedofs,freedofs) \ F(freedofs,:); 

% 受约束节点固定自由度位移值为0
U(fixeddofs,:)= 0;


% 求解单元刚度矩阵子程序 --------------------------------------------------------------
% 有限元方法计算的一个重要的系数矩阵，表征单元体的受力与变形关系;
% 特点：对称性、奇异性、主对角元素恒正、奇数（偶数）行和为0;
% 矩形单元4节点 8*8矩阵;
function [KE] = lk

% 材料杨氏弹性模量
E = 1.; 

% 材料泊松比
nu = 0.3;

k=[ 1/2-nu/6   1/8+nu/8 -1/4-nu/12 -1/8+3*nu/8 ... 
   -1/4+nu/12 -1/8-nu/8  nu/6       1/8-3*nu/8];
KE = E/(1-nu^2)*[ k(1) k(2) k(3) k(4) k(5) k(6) k(7) k(8)
                  k(2) k(1) k(8) k(7) k(6) k(5) k(4) k(3)
                  k(3) k(8) k(1) k(6) k(7) k(4) k(5) k(2)
                  k(4) k(7) k(6) k(1) k(8) k(3) k(2) k(5)
                  k(5) k(6) k(7) k(8) k(1) k(2) k(3) k(4)
                  k(6) k(5) k(4) k(3) k(2) k(1) k(8) k(7)
                  k(7) k(4) k(5) k(2) k(3) k(8) k(1) k(6)
                  k(8) k(3) k(2) k(5) k(4) k(7) k(6) k(1)];

公式汇总

柔度最小目标函数

 

\left.\begin{array}{rl} \min _{\mathbf{x}}: & c(\mathbf{x})=\mathbf{U}^{T} \mathbf{K} \mathbf{U}=\sum_{e=1}^{N}\left(x_{e}\right)^{p} \mathbf{u}_{e}^{T} \mathbf{k}_{0} \mathbf{u}_{e} \\ \text { subject to }: & \frac{V(\mathbf{x})}{V_{0}}=f \\ : & \mathbf{K U}=\mathbf{F} \\ : & \mathbf{0}<\mathbf{x}_{\min } \leq \mathbf{x} \leq \mathbf{1} \end{array}\right\}

 

 （1）
OC准则优化更新

 

\begin{aligned} &x_{e}^{\text {new }}=\\ &\left\{\begin{array}{c} \max \left(x_{\min }, x_{e}-m\right) \text { if } x_{e} B_{e}^{\eta} \leq \max \left(x_{\min }, x_{e}-m\right) \\ x_{e} B_{e}^{\eta} \text { if } \max \left(x_{\min }, x_{e}-m\right)<x_{e} B_{e}^{\eta}<\min \left(1, x_{e}+m\right) \\ \min \left(1, x_{e}+m\right) \text { if } \min \left(1, x_{e}+m\right) \leq x_{e} B_{e}^{\eta} \end{array}\right. \end{aligned}

 

 （2）
 

 

B_{e}=\frac{-\frac{\partial c}{\partial x_{e}}}{\lambda \frac{\partial V}{\partial x_{e}}}

 

 （3）
目标函数灵敏度

 

\frac{\partial c}{\partial x_{e}}=-p\left(x_{e}\right)^{p-1} \mathbf{u}_{e}^{T} \mathbf{k}_{0} \mathbf{u}_{e}

 

 （4）
灵敏度滤波

 

\frac{\widehat{\partial c}}{\partial x_{e}}=\frac{1}{x_{e} \sum_{f=1}^{N} \hat{H}_{f}} \sum_{f=1}^{N} \hat{H}_{f} x_{f} \frac{\partial c}{\partial x_{f}}

 

 （5）
卷积算子(加权因子)

 

\begin{array}{l} \hat{H}_{f}=r_{\min }-\operatorname{dist}(e, f) \\ \left\{f \in N \mid \operatorname{dist}(e, f) \leq r_{\min }\right\}, \quad e=1, \ldots, N \end{array}

 

 （6）

单元刚度矩阵

程序里最后一部分子程序，详细请学习有限元的基础知识：平面四节点矩形单元的单元刚度矩阵推导。

拓扑优化99行代码_画拓扑图的软件免费版

参考资料

[1] Sigmund, O. A 99 line topology optimization code written in Matlab. Struct Multidisc Optim 21, 120–127 (2001).

版权声明：本文为博主原创文章，转载请附上原文出处链接和本声明。

本文链接：TopOpt | 99行拓扑优化程序完全注释

今天的文章拓扑优化99行代码_画拓扑图的软件免费版分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：http://bianchenghao.cn/75082.html

赞 (0)
编程小号编程小号
0

相关推荐

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注