c语言杨辉三角形_c++杨辉三角形程序「建议收藏」

目录

一、什么是杨辉三角？

二、实现方法

1、直角三角形版

1.1、法一  观察法

1.2、法二  部分棋盘打印法

2、等腰三角形版

一、什么是杨辉三角？

特征：图形两条斜边都是由数字1组成的，而其余的数则是等于它肩上的两个数之和。

如图：

二、实现方法

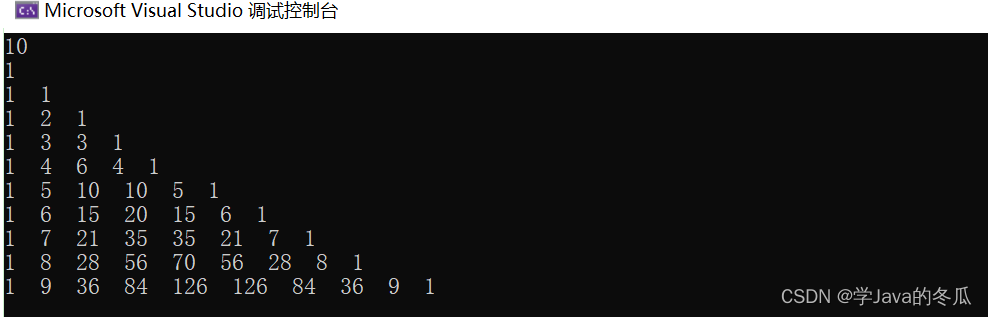
1、直角三角形版

 注意当把它的全部元素左对齐，就可以看成近似杨辉三角的样子

如图：

1.1、法一  观察法

观察图片，找i==j行和第一列j==0时直接赋值为1

其他数等于肩上两数之和

//法一  观察初始化
int main()
{
	int i = 0;
	int j = 0;
	int n = 0;
	scanf("%d", &n);
	int a[10][10] = { 0 };
    //存放元素
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)
		{
			if (j == 0 || i == j)  //第一列和i==j时直接赋值为1
			{
				a[i][j] = 1; 
			}
			if (i >= 2 && j >= 1)
			{
				a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
			}
		}
	}
    //打印
	for (i = 0; i < n; i++)
	{
		for (j = 0; j <=i; j++)
		{
			printf("%d ", a[i][j]);
		}
		printf("\n");
	}
	return 0;
}

1.2、法二  部分棋盘打印法

利用扫雷打印棋盘的方法，数组多创建行列多创建两行两列的方式，防止数组越界（也可以行+1，列+1，因为最后一行的下一行，列最后一行下一行（和正规杨辉三角不同）不会用到，没有越界问题）

//法二 采用扫雷初始化的方法，把数组空间行和列各创建大一行，防止越界
int main()
{
	int a[10][10] = { 0 };
	int i = 0;
	int j = 0;
	int n = 0;
	a[0][0] = 1;
	//输入数字
	scanf("%d", &n);
	for (i = 1; i <= n; i++)  //实际使用的数组大小是a[n+1][n+1]，多用到i=0行j=0列，但不打印出来
	{
		for (j = 1; j <= i; j++)
		{
			a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
		}
	}
	//打印
	for (i = 1; i <= n; i++)
	{
		for (j = 1; j <= i; j++)
		{
			printf("%d  ", a[i][j]);
		}
		printf("\n");
	}

	return 0;
}

成果展示：

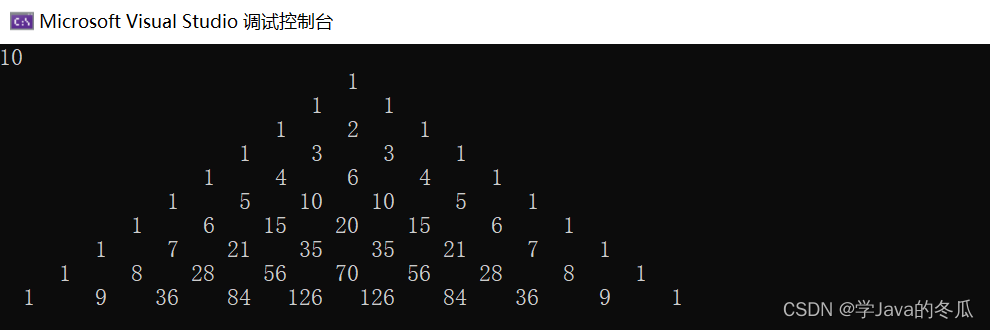
2、等腰三角形版

1、利用扫雷打印棋盘的方法，数组多创建两行两列（或者行+1，列+2，因为最后一行的下一行不会用到，而列的要用到）

2、数组空间可以自己改大再去看更大的杨辉三角

3、打印出来的空格处在数组中其实是已经初始化为0，打印时当满足数组元素==0，就打印空格

代码如下：

//法三   正规杨辉三角   (防止越界行多创建一行，列多创建两列)
//保存数据
void set(int a[10+1][2 * 10 + 1], int n)   //[][]和a本身空间要一致，不然行列数会发生变化
{
	int i = 0;
	int j = 0;
	a[1][n] = 1;
	for (i = 1; i <=n ; i++)
	{
		for (j = 1; j <= 2 * n - 1; j++)
		{
			if (i == 1 && j == n)
				continue;
			else
			    a[i][j] = a[i - 1][j - 1] + a[i - 1][j + 1];
		}
	}

}
//初始化
void Init(int a[10+1][2 * 10 + 1], int n)
{
	int i = 0;
	int j = 0;
	for (i = 0; i < n+1; i++)
	{
		for (j = 0; j < 2 * n + 1; j++)
		{
			a[i][j] = 0;
		}
	}
}
//打印
void print(int a[10+1][2 * 10 + 1], int n)
{
	int i = 0;
	int j = 0;
	for (i = 1; i <= n; i++)
	{
		for (j = 1; j <= 2 * n - 1; j++)   //最右边一列不打印
		{
			if (a[i][j] == 0)
			{
				printf("   ");  //3个空格，格式好看
			}
			else
			{
				printf("%3d", a[i][j]);  //占3个字符，格式好看
			}
		}
		printf("\n");
	}
}
int main()
{
	int n = 0;              //a[i][j] = a[i - 1][j - 1] + a[i - 1][j + 1] - 2 * '0';
	scanf("%d", &n);   //char的数组算，当字符大于'9'后会出问题
	int  a[10+1][2*10+1] = { 0 };  //画图后发现：行=n+1，因为和最后一行的下一行无关
	Init(a, n);                                        // 列=2*n+1  ，多创建两行列
	set(a, n);
	print(a, n);

	return 0;
}

成果展示：

今天的文章c语言杨辉三角形_c++杨辉三角形程序「建议收藏」分享到此就结束了，感谢您的阅读。