高斯消元法详解_高斯消元法算法流程图

1.概述

高斯消元法(Gaussian elimination)是求解线性方阵组的一种算法，它也可用来求矩阵的秩，以及求可逆方阵的逆矩阵。它通过逐步消除未知数来将原始线性系统转化为另一个更简单的等价的系统。它的实质是通过初等行变化(Elementary row operations)，将线性方程组的增广矩阵转化为行阶梯矩阵(row echelon form).

2.原理

已知线性方程组:
                                                                    
首先，要将以下的等式中的消除，然后再将以下的等式中的消除。这样可使整个方程组变成一个三角形似的格式。之后再将已得出的答案一个个地代入已被简化的等式中的未知数中，就可求出其余的答案了。所以我们可以用初等行变换把增广矩阵转换为行阶梯阵，然后回代求出方程的解。

3.求解过程

已知线性方程组:
                                                                
①.构造增广矩阵，即系数矩阵A增加上常数向量b(A|b).

                                                               
②.通过以交换行、某行乘以非负常数和两行相加这三种初等变化将原系统转化为更简单的三角形式(triangular form)
   注:这里的初等变化可以通过系数矩阵A乘上初等矩阵E来实现.

③.从而得到简化的三角方阵组，这样就容易解了.

这样就完成了整个算法的初步，一个三角形的格式(指:变量的格式而言，上例中的变量各为3,2,1个)出现了。

④.这时就可以使用向后替换算法(Algorithm for Back Substitution)求解得.

这一步就是由尾至头地将已知的答案代入其他等式中的未知数。第一个答案就是:

然后就可以将代入中，立即就可得出第二个答案:

之后，将和代入之中，最后一个答案就出来了:

就是这样，这个方程组就被高斯消元法解决了。

4.总结

总结上面过程，高斯消元法其实就是下面非常简单的过程:

原线性方程组 高斯消元法 下三角或上三角形式的线性方程组前向替换算法求解(对于上三角形式，采用后向替换算法).

5.改进

上面介绍的其实是顺序消去法，即:
将Ax=b按照从上至下、从左至右的顺序化为上三角方程组，中间过程不对矩阵进行交换。

顺序消去法虽然编程操作简单，但是存在以下两方面限制:

(1).每次运算时，必须保证对角线上的元素不为0(即运算中的分母不为0)，否则算法无法继续进行。
(2).即使的值不为零，但如果绝对值很小，由于第k次运算中在分母位置，因此作除数会引起很大的误差，从而影响算法的稳定性。

正是由于顺序消去法会因为的值过小而引入计算误差，为了减少计算过程中舍入误差对方程组求解的影响，因此是否可以选择绝对值尽可能大的主元作为除数，基于这种思想就有了高斯消去法的改进型:列主元消去法和全主元消去法。

6.列(全)主元消去法

(1).列主元消去法基本思想:

在第k步消元前，先找出k行下所有第k列元素最大的非零元素，将第r行与第k行进行整行交换，这样既不影响原方程的解，也可以将绝对值最大的作为主元，放在除数的位置上，尽可能减小引入误差。

全主元消去法与列主元消去法类似，只不过列主元消去法是从第k列中选取一个最大的元素，与第k行进行交换。而全主元消去法是从第k行第k列开始的右下角矩阵中所有元素中选取一个最大的元素作为主元，同时交换r行与c列，从而保证稳定性。

(2).列主元消去的代码:

/*
*功能: 列选主元消元法 
*@Author: lzyws739307453
*@Language: C++
*@File Name: Gauss.cpp
*@Create Time: 2019年05月05日 星期日
*/
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 5;
//输出矩阵
void printM(double a[][MAXN], int n) {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n + 1; j++)
            printf("%10f,", a[i][j]);
        printf("\n");
    }
}
//选择列主元并进行消元
void SelectColE(double a[][MAXN], int n) {
    double temp; //用于记录消元时的因数
    for (int i = 1; i <= n; i++) {
        int r = i;
        for (int j = i + 1; j <= n; j++)
            if (fabs(a[j][i]) > fabs(a[r][i]))
                r = j;
        if (r != i)
            for (int j = i; j <= n + 1; j++)
                swap(a[i][j], a[r][j]);//与最大主元所在行交换
        for (int j = i + 1; j <= n; j++) {//消元
            temp = a[j][i] / a[i][i];
            for (int k = i; k <= n + 1; k++)
                a[j][k] -= a[i][k] * temp;
        }
        printf("第%d列消元后：\n", i);
        printM(a, 3);
    }
}
//高斯消元法(列选主元)
void Gauss(double a[][MAXN], int n) {
    SelectColE(a, n);//列选主元并消元成上三角
    printf("上三角的结果：\n");
    printM(a, 3);
    for (int i = n; i >= 1; i--) {//回代求解
        for (int j = i + 1; j <= n; j++)
            a[i][n + 1] -= a[i][j] * a[j][n + 1];
        a[i][n + 1] /= a[i][i];
    }
}
//测试函数
int main() {
    double a[4][MAXN] = {
        {0,   0,   0,   0,   0},
        {0,   2,   1,  -1,   8},
        {0,  -3,  -1,   2, -11},
        {0,  -2,   1,   2,  -3}
    };
    Gauss(a, 3);
    for (int i = 1; i <= 3; i++)
        printf("X%d = %9f\n", i, a[i][4]);
    return 0;
}

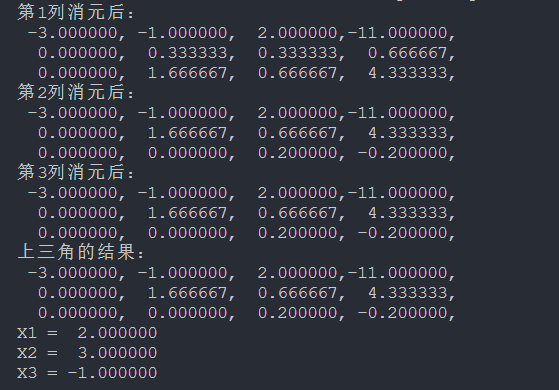
(3).运行结果:

今天的文章高斯消元法详解_高斯消元法算法流程图分享到此就结束了，感谢您的阅读。