floyd求最短路径例题_走完所有点的最短路径算法

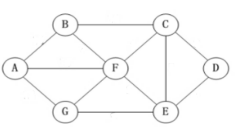
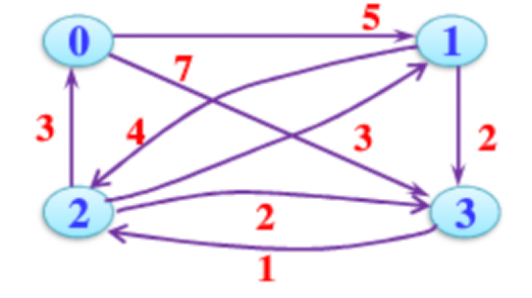
对于无权的图来说：

若从一顶点到另一顶点存在着一条路径，则称该路径长度为该路径上所经过的边的数目，它等于该路径上的顶点数减1。

由于从一顶点到另一顶点可能存在着多条路径，每条路径上所经过的边数可能不同，即路径长度不同，我们把路径长度最短（即经过的边数最少）的那条路径叫做最短路径，其路径长度叫做最短路径长度或最短距离。

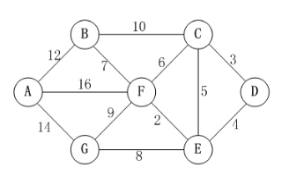
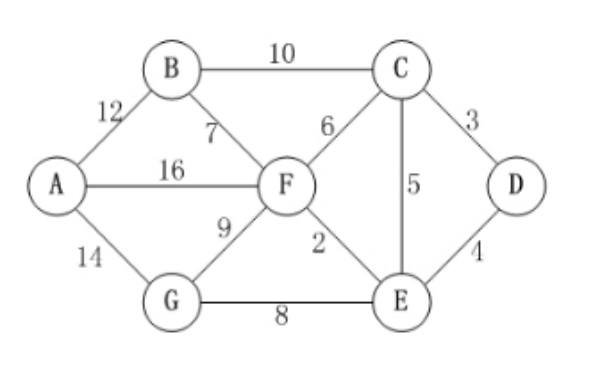
对于带权的图来说：

考虑路径上各边上的权值，则通常把一条路径上所经边的权值之和定义为该路径的路径长度或称带权路径长度。

 从源点到终点可能不止一条路径，把带权路径长度最短的那条路径称为最短路径，其路径长度（权值之和）称为最短路径长度或者最短距离。

Floyd算法

Floyd算法（Floyd-Warshall algorithm）又称为弗洛伊德算法、插点法，是解决给定的加权图中顶点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

适用范围：无负权回路即可，边权可正可负，运行一次算法即可求得任意两点间最短路。

优缺点：

Floyd算法适用于APSP(AllPairsShortestPaths)，是一种动态规划算法，稠密图效果最佳，边权可正可负。此算法简单有效，由于三重循环结构紧凑，对于稠密图，效率要高于执行|V|次Dijkstra算法。

优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单

缺点：时间复杂度比较高，不适合计算大量数据。

时间复杂度:O(n^3)；空间复杂度:O(n^2)；

任意节点i到j的最短路径两种可能：

1. 直接从i到j；
2. 从i经过若干个节点k到j。

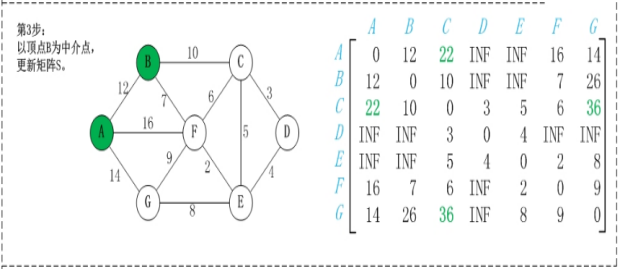
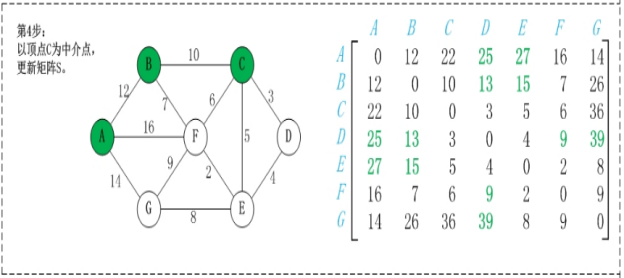
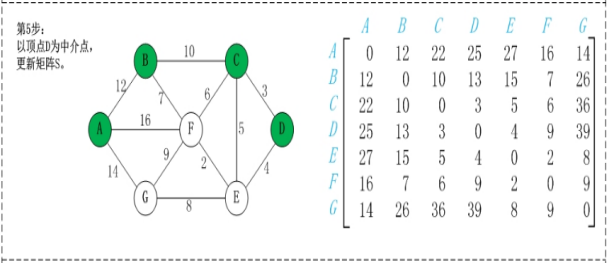
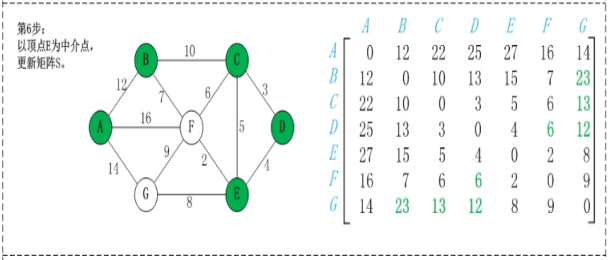
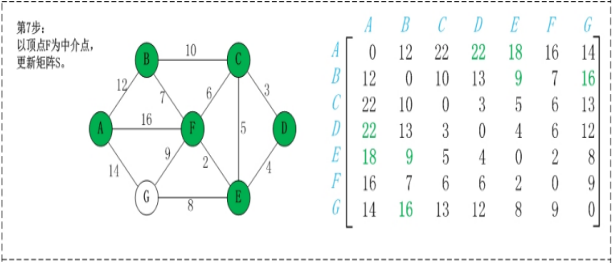
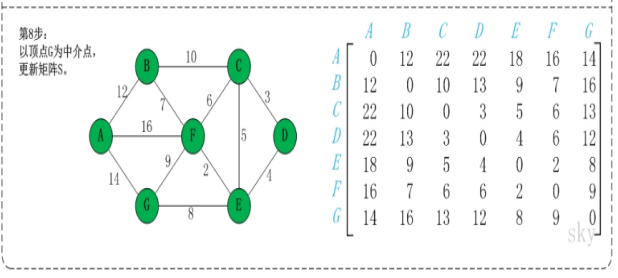
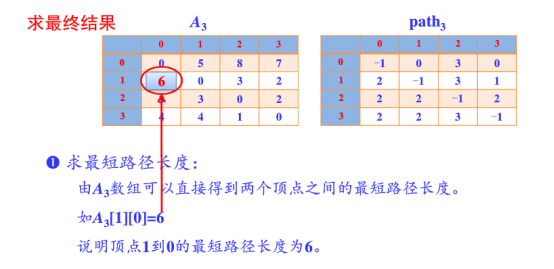
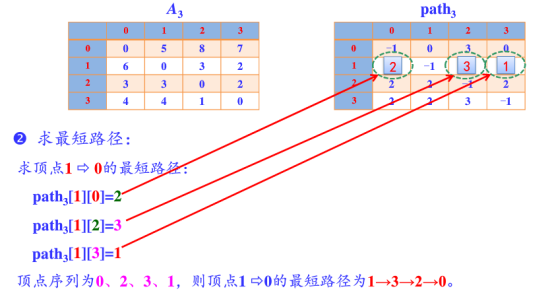
map（i，j）表示节点i到j最短路径的距离，对于每一个节点k，检查map（i，k）+map（k，j）小于map(i，j),如果成立，map（i，j） = map（i，k）+map（k，j）；遍历每个k，每次更新的是除第k行和第k列的数。

步骤：

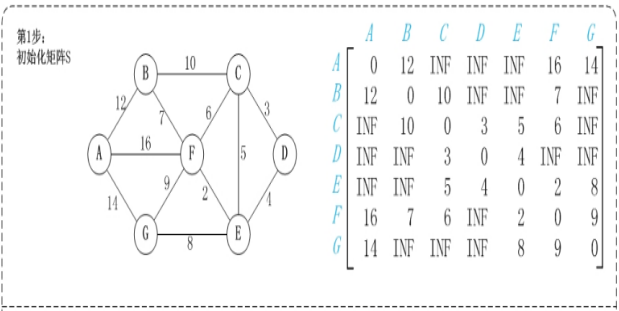
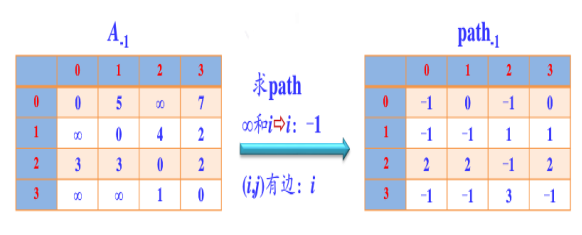
第1步：初始化map矩阵。
矩阵中map[i][j]的距离为顶点i到顶点j的权值；

如果i和j不相邻，则map[i][j]=∞。

如果i==j，则map[i][j]=0;                                          
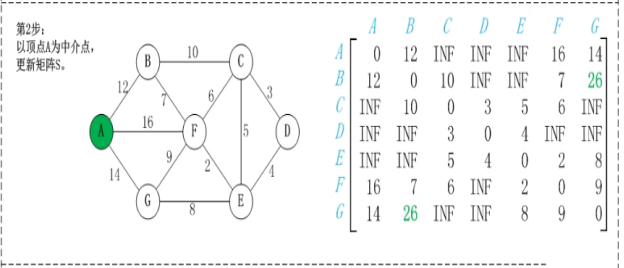
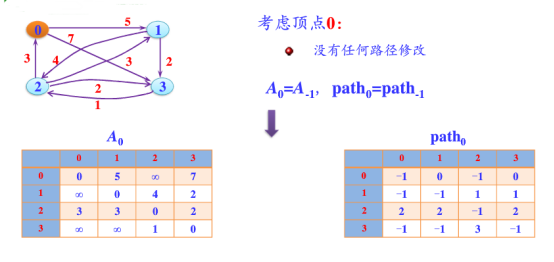
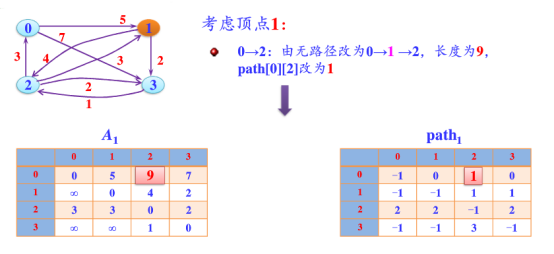
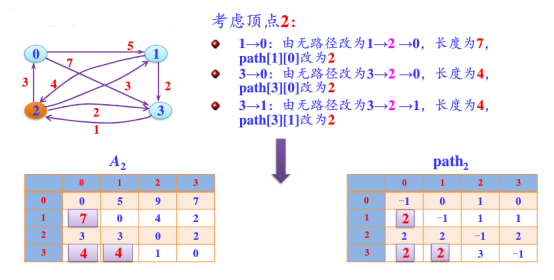
第2步：以顶点A(假设是第1个顶点)为中介点，若a[i][j] > a[i][1]+a[1][j]，则设置a[i][j]=a[i][1]+a[1][j]。

无向图构建最短路径长度邻接矩阵：

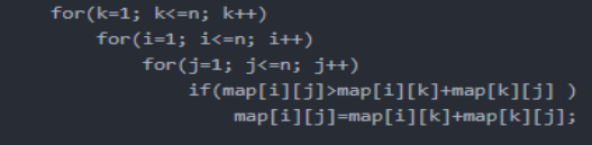
核心代码：

有向图构建最短路径长度邻接矩阵：

步骤：

核心代码：

今天的文章floyd求最短路径例题_走完所有点的最短路径算法分享到此就结束了，感谢您的阅读。