13 MATLAB判别分析

更多MATLAB数据分析视频请点击，或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016

更多MATLAB数据分析视频请点击，或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016

判别分析是对未知类别的样本进行归类的一种方法。虽然也是对样品进行分类，但它与聚类分析还是不同的。聚类分析的研究对象还没有分类，就是要根据抽样的样本进行分类，而判别分析的研究对象已经有了分类，只是根据抽样的样本建立判别公式和判别准则，然后根据这些判别公式和判别准则，判别未知类别的样品所属的类别。

 判别分析有着非常广泛的应用，比如在考古学上，根据出土物品判别墓葬年代，墓主人身份，性别；在医学上，根据患者的临床症状和化验结果判断患者疾病的类型；在经济上，根据各项经济发展指标判断一个国家经济发展水平所属的类型；在模式识别领域，用来进行文字识别，语音识别，指纹识别等。

 我们这章的主要内容是距离判别和贝叶斯判别

1.距离判别

1.1 马氏距离(Mahalanobis距离)

  马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的(scale-invariant)，即独立于测量尺度。对于一个均值为μ，协方差矩阵为Σ的多变量向量，其马氏距离为sqrt( (x-μ)’Σ^(-1)(x-μ) )。

 定义x，y之间的平方马氏距离为

     d^2(x,y)=(x-y)’Σ^(-1)(x-y)

  定义x到总体G的平方马氏距离为

   d^2(x,G)=(x-μ)’Σ^(-1)(x-μ)

1.2 两总体距离判别

 设有两个p维总体G1和G2，分布的均值向量分布为u1,u2,协方差矩阵分别为Σ1>0,Σ2>0。现有一未知类别的样本x，试判断x的归属

 如果  d^2(x,G1)<d^2(x,G2),则x属于G1类

 如果 d^2(x,G1)>d^2(x,G2), 则x属于G2类

 d^2(x,G1) = d^2(x,G2)，待判

1.3距离判别法的MATLAB实现

 MATLAB统计工具箱中提供了classify函数，用来对未知类别的样品进行判别，可以进行距离判别和先验分布为正态分布的贝叶斯判别。调用格式如下：

 <1> class=classify(sample,training,group)

  将sample中的每一个观测归入training中观测所在的某个组。输入参数sample是待判别的样本数据矩阵，training是用于构成判别函数的训练样本数据矩阵，他们的每一行对应一个观测，每一列对应一个变量，sample和training具有相同的列数。参数group是与training相应的分组变量，group和training具有相同的行数，group中的每一个元素指定了training中相应观测所在的组。group可以是一个分类变量、数值向量、字符串数组或字符串元胞数组。输出参数class是一个列向量，用来指定sample中个观测所在的组，class与group具有相同的数据类型。

 classify函数把group中的NaN或空字符串作为数据缺失数据，从而忽略training中相应的观测。

<2>class=classify(sample,training,group,type)

 可以通过type参数指定判别函数的类型，type的可能取值如下表：

<3>class=classify(sample,training,group,type,proir)

 可以通过prior参数指定各组的先验概率，默认情况下，各组先验概率相等。

<4>[class,err]=classify(……..)

  返回基于training数据的误判概率的估计值

1.4 距离判别的例子

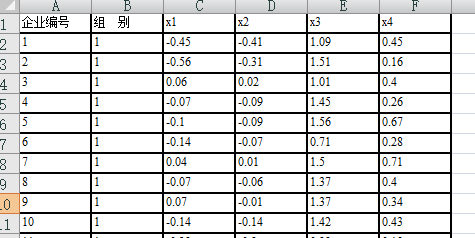
对21个破产的企业收集他们在破产前两年的年度财务数据，同时对25个财务良好的企业也收集同一时期的数据。数据涉及4个变量

x1=现金流量/总债务

x2=净收入/总资产

x3=流动资产/流动债务

x4=流动资产/净销售额

数据中，1组为破产企业，2组为非破产企业。现有4个未判企业，他们的相关数据位于表中的最后4行，根据距离判决法，对这4个未判企业进行判别。

%读取数据
%读取C2:F51范围的数据，即全部样本数据
sample = xlsread(‘企业.xls’,’C2:F51′);

%读取C2:F47范围的数据，即已知组别的样本数据
training = xlsread(‘企业.xls’,’C2:F47′);

%读取B2:B47范围的数据，即样本的分组信息
group = xlsread(‘企业.xls’,’B2:B47′);
obs = [1 : 50]’;

%距离判别
%判别函数类型为mahalanobis，返回判别结果向量C和误判概率err
[C,err] = classify(sample,training,group,’mahalanobis’);
[obs, C]
err

ans =

     1     1
     2     1
     3     1
     4     1
     5     1
     6     1
     7     1
     8     1
     9     1
    10     1
    11     1
    12     1
    13     1
    14     1
    15     2
    16     2
    17     1
    18     1
    19     1
    20     1
    21     1
    22     2
    23     2
    24     2
    25     2
    26     2
    27     2
    28     2
    29     2
    30     2
    31     2
    32     2
    33     2
    34     1
    35     2
    36     2
    37     2
    38     2
    39     2
    40     2
    41     2
    42     2
    43     2
    44     2
    45     2
    46     2
    47     1
    48     2
    49     1
    50     2

err =

    0.0676

由以上结果发现，共有3个观测发生了误判，分别为15,16和34号观测，其中第15和第16号观测由第一组误判为第二组， 而第34号观测由第2组误判为第1组。误判概率为0.0676。返回结果中第47–50号观测为未知组别的样本，由上面的结果可知，第47和第49号观测被判归为第1组，他们为破产企业；第48和第50号观测被判为第2组，他们为非破产企业。

2.贝叶斯判别法

距离判别没有考虑人们对研究对象已有的认知，而这种已有的认知可能会对判别的结果产生影响。贝叶斯判别则用一个先验概率来描述这种已有的认知，然后通过样本来修正先验概率，得到后验概率，最后基于后验概率进行判别。

2.1 贝叶斯判别的MATLAB实现

   NaiveBayes类

对于贝叶斯判别，MATLAB提供了NaiveBayes类，用户可根据训练样本创建一个NaiveBayes类对象，一个NaiveBayes类对象定义了一个朴素贝叶斯分类器，利用这个分类器可对未知类别的样品进行分类。

NaiveBayes类有很多方法和属性，如下表所列：

(1) fit 方法

fit方法用来根据训练样本创建一个朴素贝叶斯分类器对象，调用格式如下：

<1>nb=NaiveBayes.fit(training,class)

 创建一个朴素贝叶斯分类器对象nb。输入参数training是NxD的训练样本观测值矩阵，它的每一行对应一个观测，每一列代表一个变量。class是分组变量，class与training具有相同的行数，class中的每一个元素定义了training中相应观测所属的类，class中有K个不同的水平，表示K个不同的类。

<2> nb=NaiveBayes.fit(…,’param1′,val1,’param2′,val2,…..)

 通过指定可选的成对出现的参数名与参数值来控制所创建的朴素贝叶斯分类器对象。可用的参数名与参数值如下：

（2）predict方法

  在用fit方法根据训练样本创建一个朴素贝叶斯分类器对象后，可以利用对象的predict方法对待判样品进行分类。predict方法的调用格式如下：

 <1>cpre=predict(nb,test)

 根据朴素贝叶斯分类器对象nb对test中的样品(观测)进行分类，并返回分类结果向量cpre。输入参数test是N行，nb.ndims列的矩阵，这里N表示test中观测的个数，test的每一行对应一个观测，每一列对应一个变量。cpre是Nx1的向量，它与nb.CLassLevels具有相同的数据类型，其元素为test中相应观测所属的标识。

<2>cpre=predict(….,’HandleMissing’,val)

  指定缺失数据的处理方式，即对含有NaN的观测进行判别的方式。输入参数val可能取值为‘off’（默认情况）或‘on’，若为‘off’，则不对含有NaN的观测数据进行判别；若val取值为‘on’，则对含有NaN但不全为NaN的观测进行判别，此时用该观测中非NaN的列进行判别，相应的后验概率的对数为NaN。

2.2 贝叶斯判别示例

  Fisher于1936年发表的鸢尾花数据被广泛的作为判别分析的例子。数据是对刚毛鸢尾花(setosa类)，变色鸢尾花（versicolor类）和弗吉尼亚鸢尾花(virginica类)3种鸢尾花各抽取一个容量为50的样本，测量其花萼长x1，花萼宽x2，花瓣长x3，花瓣宽x4，单位为cm。数据保存在MATLAB统计工具箱文件夹下的文件fisheriris.mat中。现有10个未知类别的鸢尾花数据，如下表所示

试把fisheriris.mat中的数据作为训练样本，根据贝叶斯判别法对表中待判样品进行判别。

(1)数据导入

将文件fisheriris.mat中数据导入MATLAB工作空间

load fisheriris

此时MATLAB工作空间中多了两个变量：meas和species，其中meas是150行、4列的矩阵，对应150个已知类别的鸢尾花的4个变量的观测数据；species是150行，1列的字符串元胞向量，依次对应于150个鸢尾花所属的类，species中用字符串‘setosa’，‘versicolor’和‘virginica’表示3个不同的类。通过下面的命令查看他们的数据

head0 = {‘Obj’, ‘x1’, ‘x2’, ‘x3’, ‘x4’, ‘Class’};%设置表头
[head0; num2cell([[1:150]’, meas]), species] %以元胞数组形式查看数据

ans =

    ‘Obj’    ‘x1’        ‘x2’        ‘x3’        ‘x4’        ‘Class’     
    [  1]    [5.1000]    [3.5000]    [1.4000]    [0.2000]    ‘setosa’    
    [  2]    [4.9000]    [     3]    [1.4000]    [0.2000]    ‘setosa’    
    [  3]    [4.7000]    [3.2000]    [1.3000]    [0.2000]    ‘setosa’    
    [  4]    [4.6000]    [3.1000]    [1.5000]    [0.2000]    ‘setosa’    
    [  5]    [     5]    [3.6000]    [1.4000]    [0.2000]    ‘setosa’   
 ………………

因为meas为矩阵，而species为元胞向量，为了将meas和species放在一起以元胞数组形式查看数据，先设置表头head0，然后在mean矩阵的左边增加一列观测序号，并用num2cell函数将其转换为元胞数组，这样就可以放在一起以元胞数组形式查看数据了。

(2) 贝叶斯判别

 分类矩阵是评估预测结果的重要工具，因为它使得结果更易于理解并说明错误预测的影响。通过查看此矩阵中每个单元的数量和百分比，可以快速查看模型做出准确预测的频率。 

“分类矩阵”通过确定预测值是否与实际值匹配，将模型中的所有事例分为不同的类别。然后会对每个类别中的所有事例进行计数，并在矩阵中显示总计。 分类矩阵是评估统计模型的标准工具，有时被称为“混淆矩阵”。MATLAB中提供了confusionmat 函数得到混淆矩阵，这个函数有两个输入参数，一个是预测值，一个是实际值

[CLMat, order] = confusionmat(G1, G2)：

这个函数有两个输入参数，一个是预测值，一个是实际值

输出CLmat是混淆矩阵，order是分类的种类

matlab计算得到的混淆矩阵：

%用meas和species作为样本，创建一个朴素贝叶斯分类器对象ObjBayes
ObjBayes = NaiveBayes.fit(meas, species);

%利用创建的朴素贝叶斯分类器对象对训练样本进行判别
%返回判别结果pre0，pre0也是字符串元胞向量
%然后用pre0与species比较，观察判别的失败率
pre0 = ObjBayes.predict(meas);

%利用confusionmat函数，并根据species和pre0创建混淆矩阵
[CLMat, order] = confusionmat(species, pre0);

%以元胞数组形式查看混淆矩阵
[[{‘From/To’},order’];order, num2cell(CLMat)]

ans =

    ‘From/To’       ‘setosa’    ‘versicolor’    ‘virginica’
    ‘setosa’        [    50]    [         0]    [        0]
    ‘versicolor’    [     0]    [        47]    [        3]
    ‘virginica’     [     0]    [         3]    [       47]

从结果中可以看出，setosa类中的50个样品都得到了正确的判别，versicolor类中有47个样品得到了正确的判别，还有3个样品被错误的判到virginica类，而virginica类中也有3个发生了误判，被判到versicolor类。

下面查看是哪些样品发生了误判，需要用到grp2idx函数

[G,GN] = grp2idx(S)，G是一个关于聚类变量S的一个索引向量，GN是类别

% 查看误判样品编号
%根据分组变量pre0生成一个索引向量，gindex1
[gindex1,gn1] = grp2idx(pre0);
%根据分组变量species生成一个索引向量，gindex2
[gindex2,gn2] = grp2idx(species);
%通过对比两个索引向量，返回误判样品的观测序号向量
errid = find(gindex1 ~= gindex2)

errid =

    53
    71
    78
   107
   120
   134

% 查看误判样品的误判情况
%用num2cell函数将误判样本的观测序号向量errid转为元胞向量
%然后以元胞数组形式查看误判结果
head1 = {‘Obj’, ‘From’, ‘To’};%设置表头
[head1; num2cell(errid), species(errid), pre0(errid)]

ans =

    ‘Obj’    ‘From’          ‘To’        
    [ 53]    ‘versicolor’    ‘virginica’
    [ 71]    ‘versicolor’    ‘virginica’
    [ 78]    ‘versicolor’    ‘virginica’
    [107]    ‘virginica’     ‘versicolor’
    [120]    ‘virginica’     ‘versicolor’
    [134]    ‘virginica’     ‘versicolor’

从返回结果可以发现，第53、71、78、107、120和134号观测发生了误判，具体误判情况为：第53,71和78号观测由‘versicolor’类误判到‘virginica’类，第107、120和134号观测由‘virginica’类误判到‘versicolor’类

对表中10个未判样品进行判别

% 对未知类别样品进行判别
%定义未判样品观测数值矩阵x
x = [5.8    2.7    1.8    0.73
    5.6    3.1    3.8    1.8
    6.1    2.5    4.7    1.1
    6.1    2.6    5.7    1.9
    5.1    3.1    6.5    0.62
    5.8    3.7    3.9    0.13
    5.7    2.7    1.1    0.12
    6.4    3.2    2.4    1.6
    6.7    3    1.9    1.1
    6.8    3.5    7.9    1
    ];
%利用所创建的朴素贝叶斯分类器对象对未判样品进行判别。
%返回判别结果pre1也是字符串元胞向量
pre1 = ObjBayes.predict(x)

pre1 =

    ‘setosa’
    ‘versicolor’
    ‘versicolor’
    ‘virginica’
    ‘virginica’
    ‘versicolor’
    ‘setosa’
    ‘versicolor’
    ‘versicolor’
    ‘virginica’

pre1各元胞中的字符串依次列出了各个未判样品被判归的类。

更多MATLAB数据分析视频请点击，或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016

今天的文章13 MATLAB判别分析分享到此就结束了，感谢您的阅读。