灰度共生矩阵计算实例_灰度共生矩阵纹理特征提取

保姆级别教程，获取图片的Glcm和基于Glcm的纹理特征,附讲解思路,python代码的实现
网络上Glcm的原理很多,但是实现的python代码我确实没找到,讲的也不是很清楚
此文介绍了如何在一张图片中得到Glcm灰度共生矩阵,并基于Glcm的特征提取.带每一步的讲解

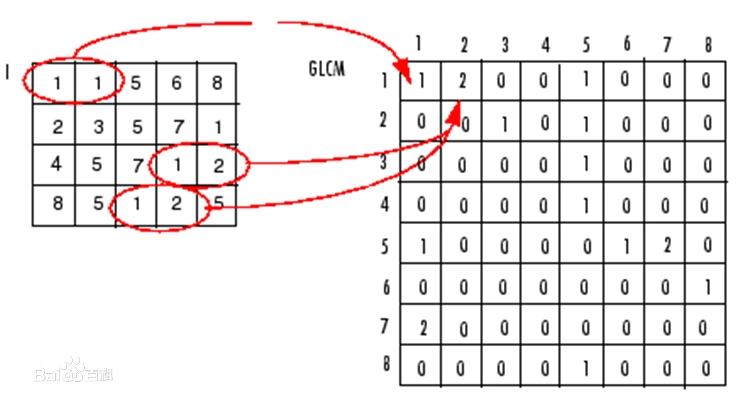
Glcm(Gray-level co-occurrence matrix) 灰度共生矩阵
原理：就是通过计算灰度图像得到它的共生矩阵，然后透过计算这个共生矩阵得到矩阵的部分特征值，来分别代表图像的某些纹理特征（纹理的定义仍是难点）。
灰度共生矩阵能反映图像灰度关于方向、相邻间隔、变化幅度的综合信息，它是分析图像的局部模式和它们排列规则的基础.
明确几个概念：方向，偏移量和灰度共生矩阵的阶数.
定义：灰度共生矩阵是图像中相距为D的两个灰度像素同时出现的联合概率分布.
意义：共生矩阵方法用条件概率来反映纹理，是相邻像素的灰度相关性的表现.

步骤：

1.opencv 读取图片 调用库cv2
2.调用skimage 的feature文件中的greycomatrix, greycoprops函数
3.将图片划分为 8个等级的灰度共生矩阵
4.依据灰度共生矩阵获得图片的特征量

import numpy as np
from skimage.feature import greycomatrix, greycoprops
import cv2
import  os
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=16) #导入本地汉字字库,pyplot显示中文

1.测试greycomatrix函数 256阶 化为 8个等级

gray = np.random.randint(0,255,(10,10))
gray,gray.shape
'''将图片的256阶化为 8个等级'''
gray_8 = (gray/32).astype(np.int32)
gray,gray_8

(array([[ 46, 221, 101, 155,  36,  46, 192, 102, 140, 197],
        [213,  47, 202, 246, 120, 204, 201, 131, 202,   1],
        [117,  52, 230, 225,  23, 249, 215, 154, 216, 225],
        [ 19, 218,  26,  92,  77, 209, 165, 206, 195,  17],
        [ 93, 116,  12,  82, 130, 225, 195, 172, 249,  39],
        [ 20,  41, 204, 144,  37, 186,  25,  47,  54, 100],
        [245, 238, 100,  91, 143, 243, 229, 180,  71, 190],
        [175,   0,  62, 218, 173, 154,  80,  51, 233,  28],
        [ 98, 115, 254,  52, 165, 250, 147, 237,  47, 246],
        [126, 156, 246,  39, 140, 119,  25, 242,   1, 198]]),
 array([[1, 6, 3, 4, 1, 1, 6, 3, 4, 6],
        [6, 1, 6, 7, 3, 6, 6, 4, 6, 0],
        [3, 1, 7, 7, 0, 7, 6, 4, 6, 7],
        [0, 6, 0, 2, 2, 6, 5, 6, 6, 0],
        [2, 3, 0, 2, 4, 7, 6, 5, 7, 1],
        [0, 1, 6, 4, 1, 5, 0, 1, 1, 3],
        [7, 7, 3, 2, 4, 7, 7, 5, 2, 5],
        [5, 0, 1, 6, 5, 4, 2, 1, 7, 0],
        [3, 3, 7, 1, 5, 7, 4, 7, 1, 7],
        [3, 4, 7, 1, 4, 3, 0, 7, 0, 6]]))

函数详解：包含主要4个参数 图片,距离(需要为列表),角度(列表),灰度等级

greycomatrix(image, distances, angles, levels=None, symmetric=False,
normed=False)
symmetric :
如果为真，则输出矩阵P[:, :, d, theta]是对称的。这一点是通过忽略数值对的顺序来实现的.
normed:
如果是 “真”，则对每个矩阵P[:, :, d, theta]进行规范化处理，方法是将其除以
除以给定偏移量的累计共现总数。
偏移量。所得矩阵的元素之和为1。
默认为假.
传参要求
：greycomatrix(image, [1], [0, np.pi/4, np.pi/2, 3*np.pi/4],
… levels=4
levels:级别数应该大于图像中的最大灰度值.

返回值：
P : 4-D ndarray
The grey-level co-occurrence histogram. The value
P[i,j,d,theta] is the number of times that grey-level j
occurs at a distance d and at an angle theta from
grey-level i. If normed is False, the output is of
type uint32, otherwise it is float64. The dimensions are:
levels x levels x number of distances x number of angles.

如下,调用灰度共生矩阵,传入参数,获得一个8灰阶的 8×8灰度共生矩阵
距离[1] 角度[0]

Glcm = greycomatrix(gray_8,[1],[0],levels=8)
Glcm_1 = Glcm.squeeze()
Glcm_1.shape,Glcm_1

((8, 8),
 array([[0, 3, 2, 0, 0, 0, 2, 2],
        [0, 2, 0, 1, 1, 2, 5, 3],
        [0, 1, 1, 1, 2, 1, 1, 0],
        [2, 1, 1, 1, 3, 0, 1, 1],
        [0, 2, 1, 1, 0, 0, 3, 4],
        [2, 0, 1, 0, 1, 0, 1, 2],
        [3, 1, 0, 2, 3, 3, 2, 2],
        [3, 4, 0, 2, 1, 1, 2, 3]], dtype=uint32))

{‘contrast’, ‘dissimilarity’,
‘homogeneity’, ‘energy’, ‘correlation’, ‘ASM’}
也就是一个Glcm 矩阵会 得到一个值

temp = greycoprops(Glcm,'ASM')
temp.shape,temp

((1, 1), array([[0.02691358]]))

def cut_img_step(img,step):  # 每个块大小为20x20
    '''传入Gray 图片与 step'''
    new_img = [] #240x240
    for i in np.arange(0, img.shape[0] + 1, step):
        for j in np.arange(0, img.shape[1] + 1, step):
            if i + step <= img.shape[0] and j + step <= img.shape[1]:
                new_img.append(img[i:i + step, j:j + step])
    new_img = np.array(new_img, dtype=np.int32)

    return new_img

好了,正式开始获取一张图片的Glcm 纹理

pwd = os.getcwd()
pwd

'D:\\_py项目文件夹\\ML-opencv-sklearn\\machine-book\\特征算子学习'

img = cv2.imread(r"../figures/guangzhou tower.jpg",cv2.IMREAD_GRAYSCALE)

'''将原图片的256阶化为 64个等级'''
level = 64
scale_data = 256/level


img_64= (img / scale_data).astype(np.int32)


plt.subplot(211)
plt.imshow(img,cmap='gray')
plt.title("256阶 675x1200",fontproperties=font)
plt.axis("off")
plt.subplot(212)
plt.imshow(img_64,cmap='gray')
plt.title("64阶 675x1200",fontproperties = font)
plt.axis("off")
plt.show()

​

如上图所示,我们使用了一张广州塔的图片,图片
Height, width
(675,1200)
这里要注意：
Float images are not supported by greycomatrix. Convert the image to an unsigned integer type.
opencv 读取图片会是float32这里需要将img_64 转为uint8类型

'''获取整张图片的Glcm纹理 4个方向 0-》3/4 pi,64阶'''
img_glcm64 = greycomatrix(img_64, [1], [0, np.pi / 4, np.pi / 2, 3 * np.pi / 4], levels=level)
'''将四个灰度共生矩阵对应相加后取 平均数得到影像的综合灰度共生矩阵'''
mean = []

for g_level1 in img_glcm64:
    for g_level2 in g_level1:
        for i in g_level2:
            mean.append(np.mean(i))

mean = np.array(mean)
'''Glcm_new 中保存了原图的Glcm4个方向的平均值'''
Glcm_new = mean.reshape(( level, level,1,1))# 后两个参数为步长数，方向数，计算特征需要


plt.subplot(211)
plt.imshow(img_64,cmap='gray')
plt.title("64阶 675x1200",fontproperties=font)
plt.axis("off")
plt.subplot(212)
plt.imshow(Glcm_new.reshape(level,level),cmap='gray')
plt.title("64阶Glcm 64x64",fontproperties = font)
plt.axis("off")
plt.show()

​

​

对角附近的元素有较大的值,说明图像的像素具有相似的像素值,
如果偏离对角线的元素会有比较大的值，说明像素灰度在局部有较大变化.

如上图,由于glcm 是一个统计量,如果我们使用pyplot 来显示图片,那么这个图片的信息实际是蕴含了一个三维的信息
[x轴,y轴,z轴],z轴是一个亮度值,x,y告诉我们位置信息
故而我们可以由这个统计的glcm分析得知,数据主要在主对角线上,也就说明
距离为1,原图4个方向上 有灰度对(x,x)的像素占绝大多少

依据Glcm提取这张图片的特征信息：
{‘contrast’, ‘dissimilarity’, ‘homogeneity’, ‘energy’, ‘correlation’, ‘ASM’}

'''注意greycoprops的传参要求 glcm 需要为[i,j,d,theta] '''
features = []
for prop in { 
   'contrast', 'dissimilarity', 'homogeneity', 'energy', 'correlation', 'ASM'}:
    features.append(greycoprops(Glcm_new, prop))#
features

[array([[0.0107847]]),
 array([[1.20763164]]),
 array([[0.10384942]]),
 array([[11.31592761]]),
 array([[0.7139315]]),
 array([[0.96871746]])]

此时我们提取了这张图片,基于glcm 的特征
提取特征后,可以使用svm支持向量机来进行分类或者其他工作
如果说觉得一张图片只是取6个特征值有点少,那咱们也可以通过其他操作来增加特征的维度
1.通过分割图片.获取特征
2.通过特征融合增加其他特征,例如灰度值

以下分享一些自己造的一些轮子

def get_glcm_sixFeature(IMG_gray):  # 传入灰度图像
    input = IMG_gray  # 读取图像，灰度模式
    # 得到共生矩阵，参数：图像矩阵，距离，方向，灰度级别，是否对称，是否标准化
    glcm = greycomatrix(input,
                        [1,2],
                        [0, np.pi / 4, np.pi / 2, np.pi * 3 / 4],
                        levels=256, symmetric=True,
                        normed=True)  # 100x100 -> 3x4

    # 得到共生矩阵统计值，官方文档
    # http://tonysyu.github.io/scikit-image/api/skimage.feature.html#skimage.feature.greycoprops
    feature = []
    feature_descrip = { 
   'contrast', 'dissimilarity',
                 'homogeneity', 'energy', 'correlation', 'ASM'}

    for prop in { 
   'contrast', 'correlation',
                 'ASM','homogeneity'  }:
        temp = greycoprops(glcm, prop)
        feature.append(temp)

    return np.array(feature), glcm


def get_gray_feature(Imgs,step= 25):
    '''格式要求 （x灰度图像二维，100，100）'''
    print(f"Imgs shape is { 
     Imgs.shape}")  #
    Imgs_number = Imgs.shape[0]
    Gray_feature_num = int((Imgs.shape[1] /step)**2)
    Avg_gray = []
    for img in Imgs:
        cut = cut_img_step(img,step)
        for patch in cut:  # 每张图4个patch
            Avg_gray.append(np.mean(patch))

    Avg_gray = np.array(Avg_gray)
    Avg_gray = Avg_gray.reshape(Imgs_number, Gray_feature_num)
    print(f'Avg_gray shape ：{ 
     Avg_gray.shape}')

    return Avg_gray

其他文章
Sober算子边缘检测与Harris角点检测1
HOG特征+SVM 进行行人检测,带源码，异常处理
线性回归预测波士顿房价

引用
灰度共生矩阵c语言实现
灰度共生矩阵 – 百度百科
原始文档

今天的文章灰度共生矩阵计算实例_灰度共生矩阵纹理特征提取分享到此就结束了，感谢您的阅读。