斐波那契数列c语言讲解_斐波那契数列性质及证明

一、斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n – 1)+F(n – 2)（n ≥ 3，n ∈ N*）

定义

斐波那契数列指的是这样一个数列：
1,1,2,3,5,8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765,
10946, 17711, 28657, 46368 ……
这个数列从第3项开始，每一项都等于前两项之和。

二、算法

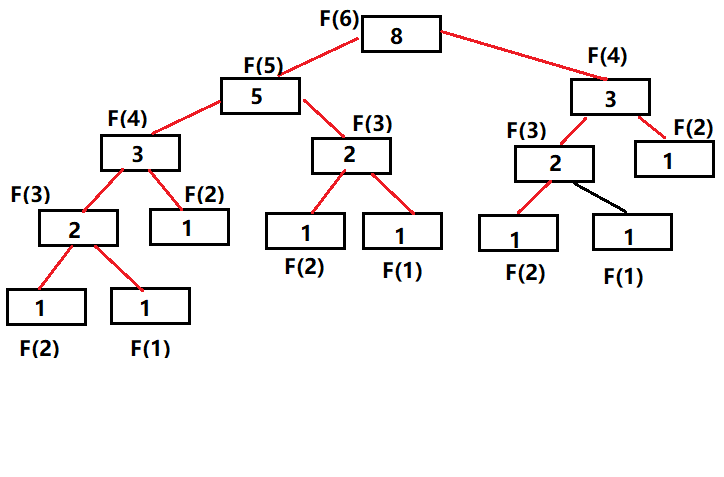
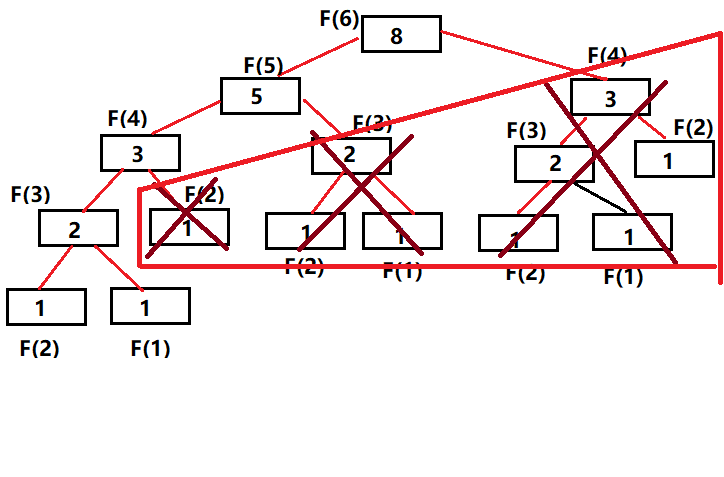
斐波那契数列的求法有递归求法和非递归求法，但通过以下对比可知，递归过程中产生很多了多余的计算，使得递归算法的时间复杂度很大，所以我们更常用非递归方法。

1.递归算法

代码

#include<stdio.h>
int fib(int n)
{ 
   
	if(n == 1 || n == 2)
		return 1;
	else
		return fib(n-1) + fib(n-2);
}
int main()
{ 
   
	int n;
	// 请勿输入过大的数字导致卡死
	scanf("%d", &n);
	printf("%d\n", fib(n));
	return 0;
}

图示

2.非递归算法

代码

#include<stdio.h>
int main()
{ 
   
	int i, n, num[10];
	num[1] = 1;
	num[2] = 1;
	for(i = 3; i < 10; i++)
		num[i] = num[i - 1] + num[i - 2];
	scanf("%d", &n);
	printf("%d", num[n]);
	return 0;
}

图示

今天的文章斐波那契数列c语言讲解_斐波那契数列性质及证明分享到此就结束了，感谢您的阅读。