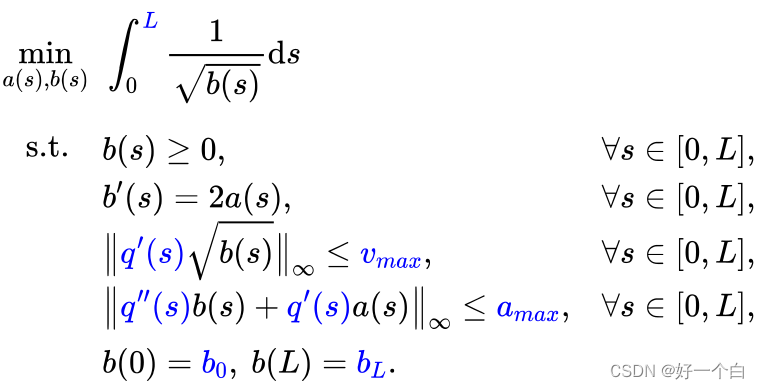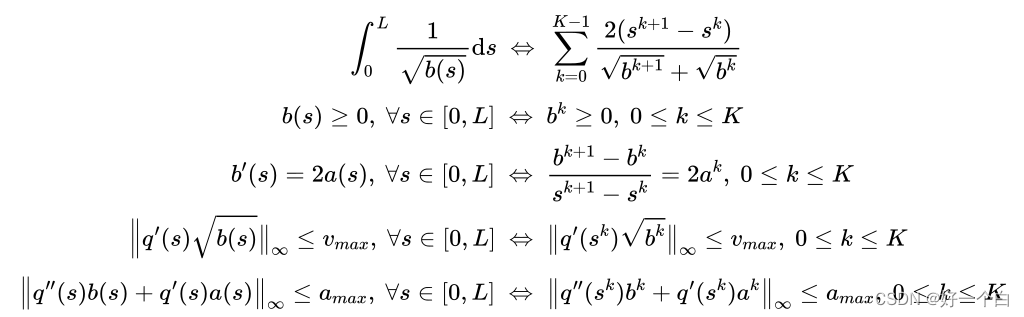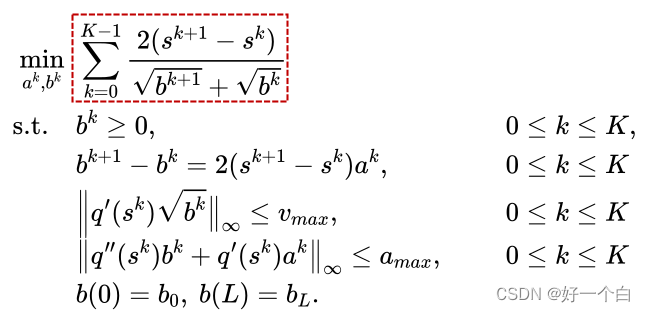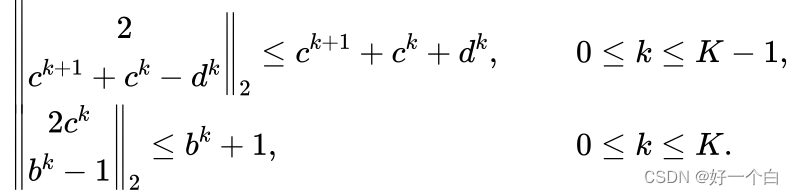TOPP问题（Time-Optimal Path Parameterization）详细解析（附代码）

题目来源

深蓝学院课程《机器人中的数值优化》（主讲：汪哲培博士）最后大作业。

参考资料

• 课程ppt与视频
• 助教和大佬的提示和讨论
• Verscheure D et al. Time-optimal path tracking for robots: A convex optimization approach. IEEE Transactions on Automatic Control. 2009 Sep 22;54(10):2318-27.

任务描述

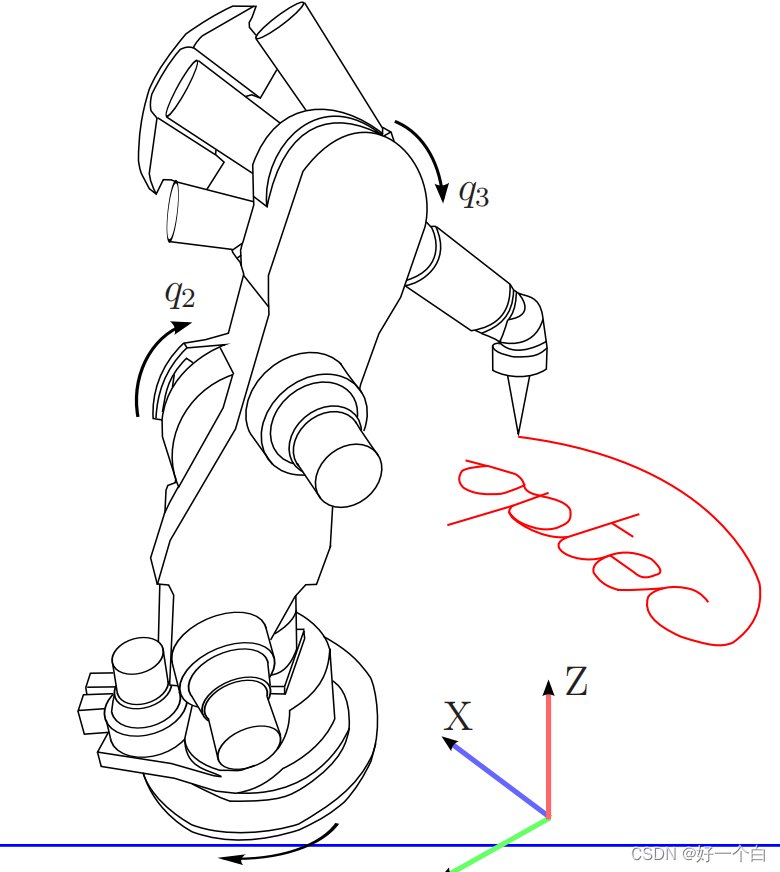
已知一个空间的路径，需要控制机械臂、无人机等去沿着它运动（如下图所示），但如何才能在满足运动约束的条件下最快地完成它呢？这就是我们要研究的问题。

该问题的整体求解思路为：

非线性控制问题建模为凸优化问题

设路径的表达方式为：随长度s变化的位置向量$q(s)$。随路径变化的速率的平方为$b(s)$，随路径参数变化的加速度大小为$a(s)$。即：

$a(s)=\frac{{\text{d}}^{2}s}{\text{d}{t}^2}$，$b(s)=(\frac{\text{d}s}{\text{d}t}{)}^2$

二者的关系为：$b^{\prime }(s)=2a(s)$，这是因为中学物理讲过的 $v_s^2-v_0^2=2as$ 。
我们最终的目标是得到时间最优的行进速率，即$\sqrt{b(s)}$ 。

优化目标最短时间可写作：

$T={\int }_0^{T}1dt={\int }_0^L\frac{1}{ds/dt}ds={\int }_0^L\frac{1}{\sqrt{b(s)}}ds$

实际速度（随时间变化）为：

$\frac{\mathrm{d}q}{\mathrm{d}t}=q^{\prime }(s)\sqrt{b(s)}$

实际加速度（随时间变化）为：

$\frac{{\mathrm{d}}^{2}q}{\mathrm{d}{t}^2}=\frac{\mathrm{d}(q^{\prime }(s)\sqrt{b(s)})}{\mathrm{d}s}\frac{\mathrm{d}s}{\mathrm{d}t}=q^{\prime \prime }(s)b(s)+q^{\prime }(s)a(s)$

然后可以得到关于以函数 $b(s),a(s)$ 为优化变量的优化问题模型：

蓝色为已知量。这个优化问题是凸的。

【为什么式凸的？：凸优化问题即目标函数和约束条件都是凸的。首先说明优化目标函数是凸的：本问题自变量为函数，则优化目标函数是凸的就是在说，任意函数$b_1(s)$和$b_2(s)$以及$0\le \theta \le 1$满足:

${\int }_0^L\frac{1}{\sqrt{\theta b_1(s)+(1-\theta )b_2(s)}}\mathrm{d}s\le \theta {\int }_0^L\frac{1}{\sqrt{b_1(s)}}\mathrm{d}s+(1-\theta ){\int }_0^L\frac{1}{\sqrt{b_2(s)}}\mathrm{d}s$

由于被积函数大于0，积分可以看作加法，为凸函数，故可把积分去掉，得到其充分条件为：

$\frac{1}{\sqrt{\theta x+(1-\theta )y}}\le \theta \frac{1}{\sqrt{x}}+(1-\theta )\frac{1}{\sqrt{y}}$

亦即$\frac{1}{\sqrt{x}}$为凸函数。该充分条件显然成立，所以目标函数为凸函数。

约束方面，导数是个线性操作，所以第二个约束是凸的。第四个约束不等号左边是无穷范数和放射变换，它们都是凸的，所以该约束是凸的。对于速度约束，该不等式等价于$||(q^{\prime }(s){)}^{2}b(s)|{|}_{\infty }\le v_{max}^2$，是线性的，所以是凸的。注：开根号是个非凸函数，与该约束是凸的并不矛盾，因为“约束是凸的”不是指左边函数是凸的，而是指解集是凸集，“左边函数是凸的”是“解集是凸的”的充分非必要条件。】

转化成离散的大规模凸优化问题

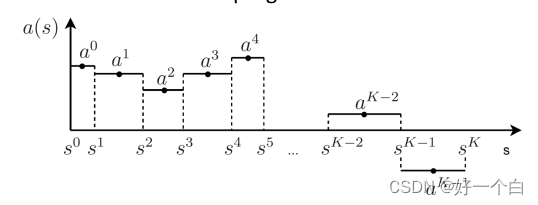
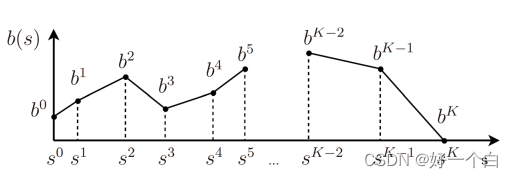
我们无法直接处理以连续函数为自变量的优化问题，所以对其进行离散：

进行如上图的离散，对于目标函数和约束分别进行离散可以得到：

【补充解释第一项：上图中离散后的线段$b^k{b}^{k+1}$表达式设为：$b(s)=\alpha s+\beta ,\alpha =\frac{b^{k+1}-b^k}{s^{k+1}-s^k}$

则$s^k{s}^{k+1}$段的积分为：

$\begin{array}{rl}{\int }_{s^k}^{s^{k+1}}\frac{1}{\sqrt{b(s)}}\mathrm{d}s& =\frac{2}{\alpha }b(s{)}^{1/2}{|}_{s^k}^{s^{k+1}}\\ & =\frac{2}{\alpha }\left(\sqrt{b^{k+1}}-\sqrt{b^k}\right)\\ & =2\frac{s^{k+1}-s^k}{b^{k+1}-b^k}\left(\sqrt{b^{k+1}}-\sqrt{b^k}\right)\\ & =2\frac{s^{k+1}-s^k}{\sqrt{b^{k+1}}+\sqrt{b^k}}\end{array}$
然后求和即可得到】

由此得到优化问题：

把离散问题转换成SOCP形式

思路大概是，通过引入一些变量进行一些紧的放缩，把表达形式凑成SOCP形式。

首先改造目标函数，增加隐变量$c^k,d^k$，其满足：

$c^k\le \sqrt{b^k}$， $\frac{1}{c^{k+1}+c^k}\le d^k$。

则可以得到$\frac{1}{\sqrt{b^{k+1}}+\sqrt{b^k}}\le d^k$，以上每一步等号都可以取到，则$\min \frac{1}{\sqrt{b^{k+1}}+\sqrt{b^k}}⟺\min d^k$，同时$b^k,c^k,d^k$需要满足上面两个约束。该约束可写作锥的形式（乘开验证即可得到）：

经过转换可以得到该优化问题的SOCP表达形式：

• 优化目标：

${\min }_{a^k,b^k,c^k,d^k}{\sum }_{k=0}^{K-1}2(s^{k+1}-s^k)d^k$ ,

• 锥约束：

${\Vert \begin{array}{c}2\\ c^{k+1}+c^k-d^k\end{array}\Vert }_2\le c^{k+1}+c^k+d^k,(0\le k\le K-1)$

${\Vert \begin{array}{c}2c^k\\ b^k-1\end{array}\Vert }_2\le b^k+1,(0\le k\le K)$

• 等式约束：

$2(s^{k+1}-s^k)a^k+b^k-b^{k+1}=0,(0\le k\le K-1)$

${\Vert q^{\prime }(s^0)\Vert }_2^2{b}^0=v_{start}^2$

${\Vert q^{\prime }(s^k)\Vert }_2^2{b}^K=v_{end}^2$

• 不等式约束：

$-b_k\le 0,(0\le k\le K)$

$\left({\left(q_y^{\prime }(s^k)\right)}^2+{\left(q_x^{\prime }(s^k)\right)}^2\right)b^k-v_{max}^2\le 0,(0\le k\le K)$

$q_x^{\prime \prime }(s^k)b^k+q_x^{\prime }(s^k)a^k-a_{max}\le 0,(0\le k\le K-1)$

$q_y^{\prime \prime }(s^k)b^k+q_y^{\prime }(s^k)a^k-a_{max}\le 0,(0\le k\le K-1)$

$-q_x^{\prime \prime }(s^k)b^k-q_x^{\prime }(s^k)a^k-a_{max}\le 0,(0\le k\le K-1)$

$-q_y^{\prime \prime }(s^k)b^k-q_y^{\prime }(s^k)a^k-a_{max}\le 0,(0\le k\le K-1)$

优化问题求解

使用锥增广拉格朗日方法求解。
增广拉格朗日函数为：

$\mathcal{L}(a,b,c,d,\lambda ,\mu ,\sigma )={\sum }_{k=0}^{K-1}2(s^{k+1}-s^k)d^k+\frac{\rho }{2}\left\{{\sum }_{i=1}^{2K+1}{\Vert {\mathcal{P}}_{k_i}\left(\frac{{\mu }_i}{\rho }-u_i\right)\Vert }^2+{\sum }_{i=1}^{K+1}{\Vert h_i(x)+\frac{{\lambda }_i}{\rho }\Vert }^2+{\sum }_{i=1}^{6K+2}{\Vert g_i(x)+\frac{{\sigma }_i}{\rho }\Vert }^2\right\}$

其中，第一类锥约束中$u_k=\left[\begin{array}{c}{c}^{k+1}+c^k+d^k\\ 2\\ c^{k+1}+c^k-d^k\end{array}\right],(0\le k\le K-1)$ ；第二类锥约束中$u_k=\left[\begin{array}{c}{b}^k+1\\ 2c^k\\ b^k-1\end{array}\right],(0\le k\le K)$。

增广拉格朗日函数每项的导数分别为：

• 目标函数：$\frac{\partial \mathcal{L}}{\partial d^k}=2(s^{k+1}-s^k)$
• 第一类锥约束：$\frac{\partial \mathcal{L}}{\partial (c^k,c^{k+1},d^k)}=\rho \left[\begin{array}{ccc}1& 1& 1\\ 0& 0& 0\\ 1& 1& -1\end{array}\right]{\mathcal{P}}_{k_i}\left(\frac{{\mu }_k}{\rho }-u_k\right)$,$u_k=\left[\begin{array}{c}{c}^{k+1}+c^k+d^k\\ 2\\ c^{k+1}+c^k-d^k\end{array}\right],(0\le k\le K-1)$
• 第二类锥约束：$\frac{\partial \mathcal{L}}{\partial (b^k,c^k)}=\rho \left[\begin{array}{ccc}1& 0& 1\\ 0& 2& 0\end{array}\right]{\mathcal{P}}_{k_i}\left(\frac{{\mu }_i}{\rho }-u_i\right)$,$u_k=\left[\begin{array}{c}{b}^k+1\\ 2c^k\\ b^k-1\end{array}\right],(0\le k\le K)$
• 其余皆为线性约束，其形如：$\frac{\partial \mathcal{L}}{\partial (b^k)}=\rho \frac{\partial h}{\partial (b^k)}\left(h_i(x)+\frac{{\lambda }_i}{\rho }\right)$。

参数更新和终止条件如ppt所示：

代码实现

从公式到代码会有很多细节不同，以下仅个人实现过程～

1. 首先明确优化变量：

设待优化变量$x=(b^0,\dots ,b^K,a^0,\dots ,a^{K-1},c^1,\dots ,c^K,d^0,\dots ,d^K)$

2. 明确已知条件

根据之前的作业，我们已经得到分段三次多项式轨迹$p(t)$，用它作为本次task的输入路径。在求解该分段轨迹的时候，我们把参数t解释为时间，把导数解释为速度，在求解过程中控制相邻多项式轨迹段端点导数们相等，即速度、加速度相等。而本问题中，要把它视作路径而不是轨迹，所以t不是时间。为减少误解，下文把自变量写作u，即路径$p(u)$。
除此之外参数还已知最大速度、最大加速度，可以是随路径长度变化的曲线。本文为方便，取为恒值。

3. 重要参数$s^k,q^{\prime }(s^k),q^{\prime \prime }(s^k)$的求解

$q(s)=p(u)$，二者函数值相同，自变量不同。为了得到离散的s，首先均匀地离散u，设每个轨迹段被分成r小段，每小段端点是$u^k$对应的点，则整条分段多项式轨迹的小段数 K = r * 多项式个数。然后按照 离散的u => p(u) => q(s) => s 的顺序得到离散的s。需要明确的是这种离散方式得到的s不是等距分布的。具体表达式为：

• 路径长度s：曲线路径被离散为分段“匀加速运动”，所以s的递推公式为$s^{k+1}=s^k+\frac{||p^{\prime }(u^k)||+||p^{\prime }(u^{k+1})||}{2}du$，$du=\frac{分段多项式轨迹中u的取值范围}{K}$。
• 位置对轨迹长度的导数$q^{\prime }(s)$：相当于路径切向单位向量，即$q^{\prime }(s)=\frac{p^{\prime }(u)}{||p^{\prime }(u)||}$
• 位置对轨迹长度的二次导数$q^{\prime \prime }(s)$：对$q^{\prime }(s)$用链式法则求导，可以得到精确值的表达式：$q_x^{\prime \prime }(s)=\left(\frac{{\mathrm{d}}^2{p}_x(u)}{\mathrm{d}{u}^2}\frac{\mathrm{d}{p}_y(u)}{\mathrm{d}u}-\frac{{\mathrm{d}}^2{p}_y(u)}{\mathrm{d}{u}^2}\frac{\mathrm{d}{p}_x(u)}{\mathrm{d}u}\right)\frac{\mathrm{d}{p}_y(u)}{\mathrm{d}u}{\left(\frac{\mathrm{d}u}{\mathrm{d}s}\right)}^4$，
  $q_y^{\prime \prime }(s)=\left(\frac{{\mathrm{d}}^2{p}_y(u)}{\mathrm{d}{u}^2}\frac{\mathrm{d}{p}_x(u)}{\mathrm{d}u}-\frac{{\mathrm{d}}^2{p}_x(u)}{\mathrm{d}{u}^2}\frac{\mathrm{d}{p}_y(u)}{\mathrm{d}u}\right)\frac{\mathrm{d}{p}_x(u)}{\mathrm{d}u}{\left(\frac{\mathrm{d}u}{\mathrm{d}s}\right)}^4$，
  其中$\frac{\mathrm{d}u}{\mathrm{d}s}=\frac{1}{||p^{\prime }(u)||}$。注意，这里有个小量的四次方倒数，实际操作中数值极不稳定。取而代之，采用精确度不高的数值微分法求解导数：$q^{\prime \prime }(s^k)=\frac{q^{\prime }(s^{k+1})-q^{\prime }(s^k)}{s^{k+1}-s^k}$，数值稳定性好很多，而且简单。

4. 代码

代码库地址：·gitee上的代码仓库
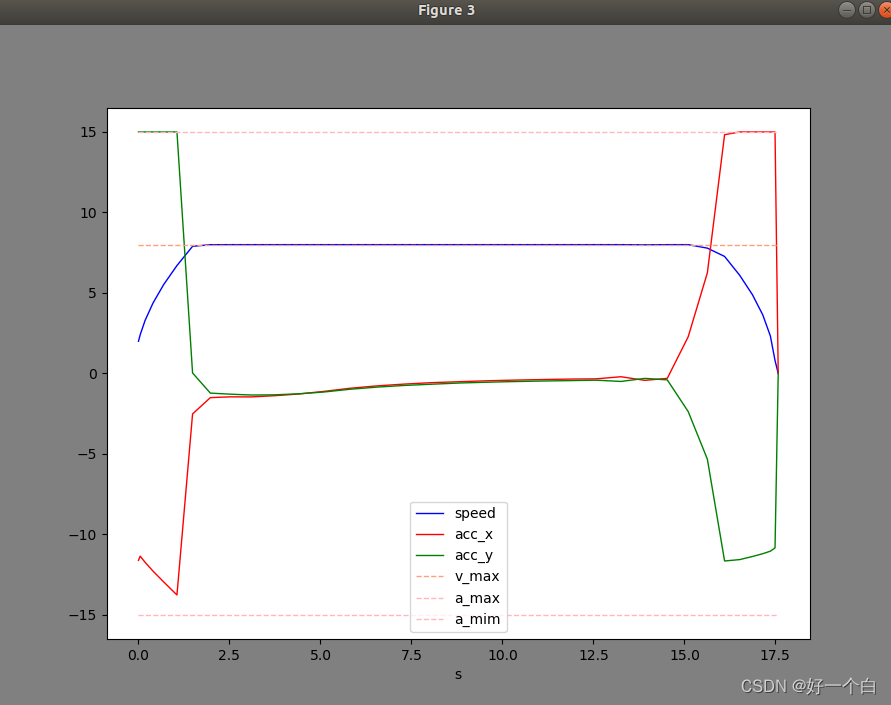
运行结果：

代码中尚存在的问题：

• 优化偶尔失败，推测原因为一些中间量求解的数值稳定性和准确度不够高。
• 理论上应该先做搜索得到全局路径，再进行轨迹优化。没有写全局路径搜索，所以测试的时候，需要初始直线路径避开死胡同。

最后并同样重要

这项任务耗时远远超过预想，陷入一些思维误区，花了好长时间捋顺思路并调通代码，希望对大家有一些帮助。另外，本人代码水平有限，如果发现本文和代码中有错误，希望可以告知我～如果代码对你有帮助并且你有更好的实现，希望可以分享一下～

今天的文章TOPP问题（Time-Optimal Path Parameterization）详细解析（附代码）分享到此就结束了，感谢您的阅读。