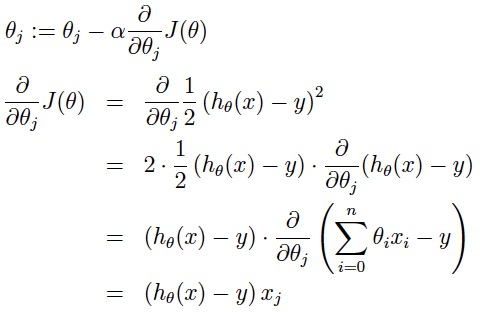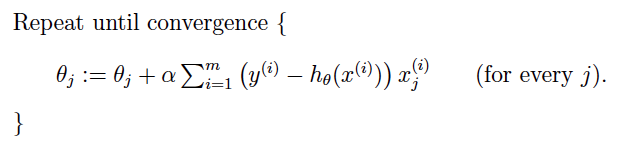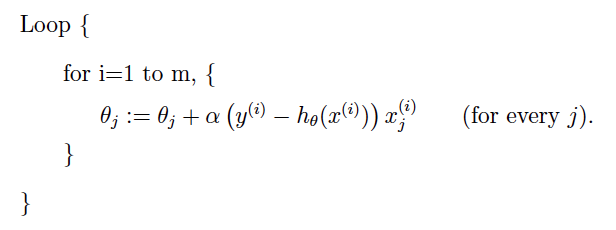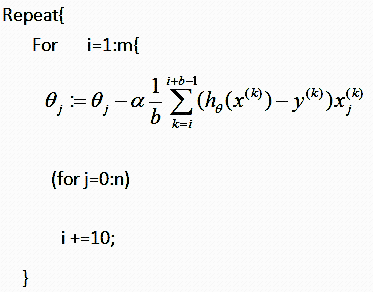深度学习数学基础(二)～随机梯度下降(Stochastic Gradient Descent, SGD)

1. 梯度

梯度gradient，矢量：即为该点最大变化方向的导数，导数方向为 $L'(\theta)$ 变大的方向，通过求导或偏导来计算梯度，即在点x处整体误差e在某一个参数w处的分误差 $e_{w_i}$ 。

$L(\theta) = f(\theta; y) - f(\theta; \hat{y}) = \Delta y$ 注意这里没有 $\Delta x$

整体误差e，即为损失函数loss，常用的有：交叉熵，最小二乘，BECLoss，e.g.。

导数值为正，表示导数方向在[0, 90度]，参数 $\theta$ 在这个方向上走一步， $L(\theta)$ 增长最快最大；导数值为负，表示导数方向[90, 180]，变化同理。结合如图所示：导数值表示变化

但是，我们的目标减小损失函数值 $L(\theta)$ ，即误差 -》逆梯度。最大化经由最小化 -f(x) 来实现。-》通常以最小化 f(x) 指代大多数最优化问题。这就是逆梯度下降(随机梯度下降)中“逆”的由来！而且加比减好做、乘比除好做、缩小比放大好做！

如图所示，我们假设函数是 ,那么如何使得这个函数达到最小值呢，简单的理解，就是对x求导，得到，然后用梯度下降的方式，如果初始值是（0的左边）负值,那么这是导数也是负值，用梯度下降的公式，使得x更加的靠近0,如果是正值的时候同理。
注意：这里的梯度也就是一元函数的导数，高维的可以直接类推之

1.1 梯度详细解释

我们把要最小化或最大化的函数称为目标函数 $h_{\theta} (x)$ 。当我们对其进行最小化时，我们也把它称为损失函数 loss function.

误差e求梯度gradient

下面，我们假设一个损失函数为 $J(\theta )=\frac{1}{2} \sum_{i=1}^{m}(h_{\theta }(x)-y)^{2}$ ，其中 $h_{\theta }(x)=\theta_{0} +\theta_{1}x_{1}+\theta_{2}x_{2}+......+\theta_{n}x_{n}$ 然后要使得最小化它。

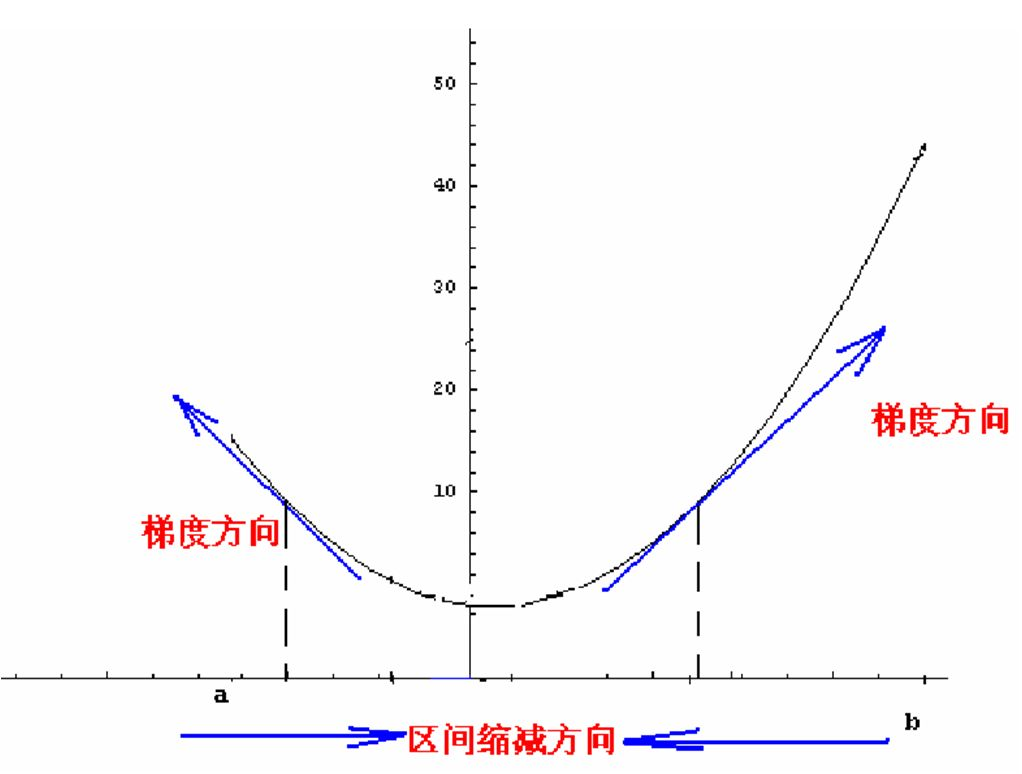
我们知道曲面上方向导数的最大值的方向就代表了梯度的方向，➡️【扩展知识：如何直观形象的理解方向导数与梯度以及它们之间的关系？】

因此我们在做梯度下降的时候，应该是沿着梯度的反方向进行权重的更新(因为梯度指的是增长最快的方向，而往下滑是减小最快的方向)，可以有效地找到全局的最优解。这个 $\theta$ 更新过程可以描述为

[a表示的是步长或者说是学习率（learning rate）]

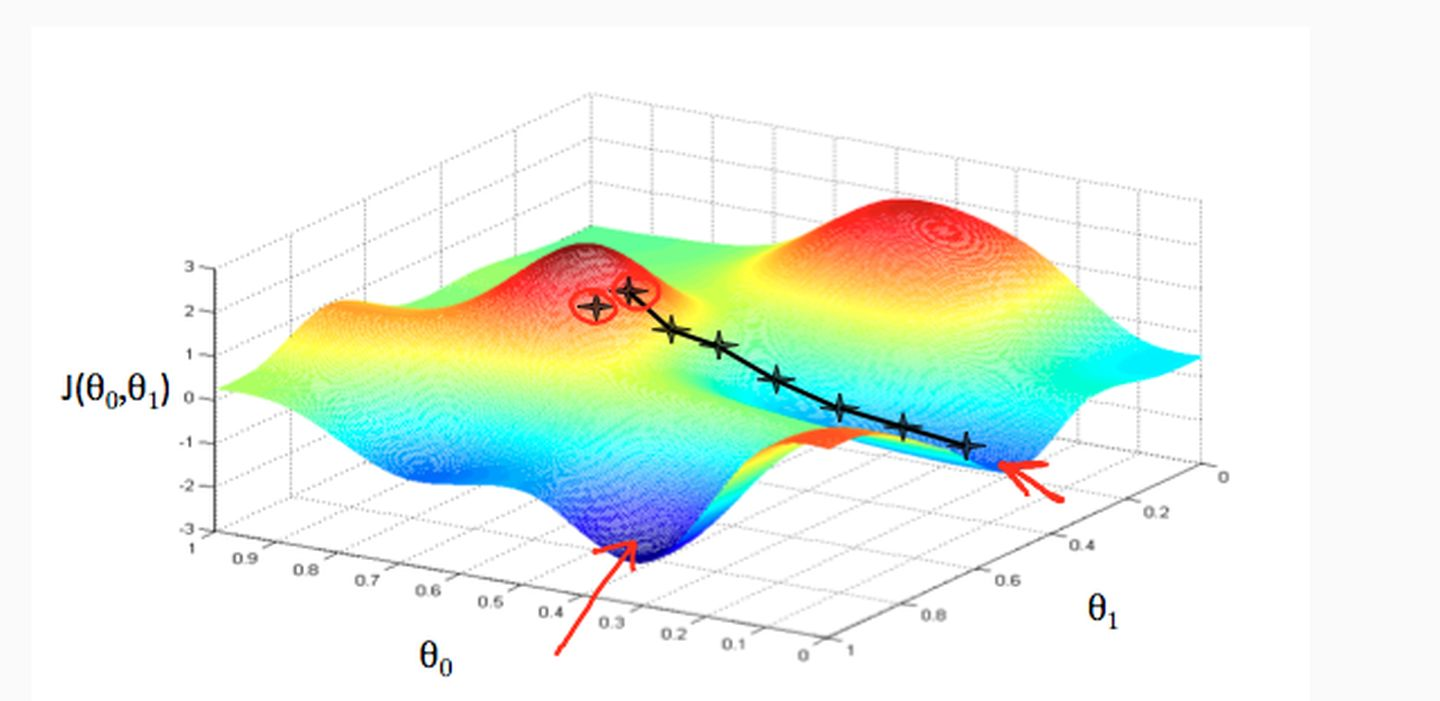
好了，怎么理解？在直观上，我们可以这样理解，看下图，一开始的时候我们随机站在一个点，把他看成一座山，每一步，我们都以下降最多的路线来下山，那么，在这个过程中我们到达山底（最优点）是最快的，而上面的 $\alpha$ ，它决定了我们“向下山走”时每一步的大小，过小的话收敛太慢—-梯度消失，过大的话可能错过最小值—-梯度爆炸。➡️【扩展知识：详解机器学习中的梯度消失、爆炸原因及其解决方法】）。这是一种很自然的算法，每一步总是寻找使J下降最“陡”的方向（就像找最快下山的路一样）。

当然了，我们直观上理解了之后，接下来肯定是从数学的角度，我们可以这样想，先想在低维的时候，比如二维，我们要找到最小值，其实可以是这样的方法，具体化到1元函数中时，梯度方向首先是沿着曲线的切线的，然后取切线向上增长的方向为梯度方向，2元或者多元函数中，梯度向量为函数值f对每个变量的导数，该向量的方向就是梯度的方向，当然向量的大小也就是梯度的大小。现在假设我们要求函数的最值，采用梯度下降法。

2. 随机逆梯度下降法 (优化器optimizer)

由上面知道，为啥用随机逆梯度下降法，减小误差/loss。

BP更新：back propogation，包括： $L(\theta)$ 求导 + 参数更新。

$L(\theta)$ 求导： $L'(\theta)$

参数更新: $\theta^{new} = \theta^{old} - \alpha \cdot L'(\theta; x; y; \hat{y})$ . 这里逆梯度的逆体现在减号-上； $\alpha$ 是学习率，即更新步长； $L'(\theta)$ 是损失函数求偏导，求导我们所在这一layer of DNN model的分导。

这种更新过程也叫优化optimization。
上面这种最简单的直接减，就是随机梯度下降方式SGD，也叫优化器optimizer。当然我们可以在导数前乘参数进行防缩、加常量进行平移，所以就产生了许许多多很有花样的更新方式，比如：SGDM，AdaGrad，Adam等！Neural Network-神经网络算法本质_nn.sequential自动更新权重_天狼啸月1990的博客-CSDN博客

但是，没经过DNN由多层神经网络，BP每经过一层，损失函数就得进行一次求导求权重w上的分误差，而最后一层的误差和前面几层的分误差是通过求导的链式法则联系的！

$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$
$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$ 这也是指数级的由来：乘*乘 *乘。0.2 * 0.2 * 0.2 = 0.008。

这每个分量都是一个loss的导数 –》“梯度消失”和梯度爆炸 -》梯度消失和梯度爆炸的根本原因来自于loss的值。-》而实际上较大的loss值来源于较大的向量值embedding values。

2.1 梯度消失和梯度爆炸

“梯度消失”和梯度爆炸 -》梯度消失和梯度爆炸的根本原因来自于loss的值。

如果求得的loss value较小。假定是3层神经网络，loss=0.2。在指数级相乘加持下，0.2 * 0.2 * 0.2 = 0.008，这就是梯度消失。因为这么小的loss，对每层神经网络上参数 $\theta$ 的影响急剧减小，直到0.008可以忽略不计了！这里可以看出梯度消失的本质是initial loss value很小。而这个很小是由embedding value很小得到得。
如果求得的loss value较大。同样假定3层神经网络，loss=200，在指数级相乘加持下，200*200*200=，这就是梯度爆炸！因为这么大的loss，对每层神经网络上参数 $\theta$ 的影响急剧变大，直到80000就不能承受了！这里同样可以得出梯度爆炸的本质是initial loss value过大。

Then，我们知道了梯度消失、梯度爆炸的原因是initial loss value太小、太大。而loss value太小、太大的原因是因为x embedding value值太小、太大！那么我们该如何抑制梯度消失和梯度爆炸呢？

2.2 梯度消失和梯度爆炸抑制方法

由上述分析得出，抑制梯度消失和梯度爆炸的根本措施是让loss value变得正常！这有两个方向可以动：参数和向量值。

2.2.1 参数方向

参数放缩

2.2.2 向量值方向

embedding values adjustment，包括：激活函数、归一化等。

激活函数：sigmoid、ReLU、ELU。这里不同的激活函数有不同的特性！没有最好的激活函数，只有最合适的激活函数！比如，sigmoid就比ReLU更好的抑制梯度爆炸。因为ReLU和ELU因为公式定义，无法处理embedding values中的较大值！
归一化函数。torch.BatchNorm1d，对梯度消失和梯度爆炸有奇效哟！

2. 优缺点比较

这里比较对象是批量梯度（Batch Gradient Descent）和mini-batch梯度下降，先看下他们三者：

2.1 批量梯度下降

批量梯度下降：在每次更新时用所有样本，要留意，在梯度下降中，对于 $\theta_{i}$ 的更新，所有的样本都有贡献，也就是参与调整 $\theta$ .其计算得到的是一个标准梯度，对于最优化问题，凸问题，也肯定可以达到一个全局最优。因而理论上来说一次更新的幅度是比较大的。如果样本不多的情况下，当然是这样收敛的速度会更快啦。但是很多时候，样本很多，更新一次要很久，这样的方法就不合适啦。下图是其更新公式

2.2 随机梯度下降

随机梯度下降：在每次更新时用1个样本，可以看到多了随机两个字，随机也就是说我们用样本中的一个例子来近似我所有的样本，来调整θ，因而随机梯度下降是会带来一定的问题，因为计算得到的并不是准确的一个梯度，对于最优化问题，凸问题，虽然不是每次迭代得到的损失函数都向着全局最优方向，但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。但是相比于批量梯度，这样的方法更快，更快收敛，虽然不是全局最优，但很多时候是我们可以接受的，所以这个方法用的也比上面的多。下图是其更新公式：

2.3 mini-batch梯度下降

mini-batch梯度下降：在每次更新时用b个样本,其实批量的梯度下降就是一种折中的方法，他用了一些小样本来近似全部的，其本质就是我1个指不定不太准，那我用个30个50个样本那比随机的要准不少了吧，而且批量的话还是非常可以反映样本的一个分布情况的。在深度学习中，这种方法用的是最多的，因为这个方法收敛也不会很慢，收敛的局部最优也是更多的可以接受！

}

了解之后，总的来说，随机梯度下降一般来说效率高，收敛到的路线曲折，但一般得到的解是我们能够接受的，在深度学习中，用的比较多的是mini-batch梯度下降。

最后是收敛性，能收敛吗？收敛到什么地方？

对于收敛性的问题，知乎上就有这个问题：为什么随机梯度下降方法能够收敛？，我比较赞赏李文哲博士的回答（推荐一看），总的来说就是从expected loss用特卡洛（monte carlo）来表示计算，那batch GD, mini-batch GD, SGD都可以看成SGD的范畴。因为大家都是在一个真实的分布中得到的样本，对于分布的拟合都是近似的。那这个时候三种方式的梯度下降就都是可以看成用样本来近似分布的过程，都是可以收敛的！

对于收敛到什么地方：

能到的地方：最小值，极小值，鞍点。这些都是能收敛到的地方，也就是梯度为0的点。

当然，几乎不存在找到鞍点的可能，除非很碰巧，因为梯度下降是对损失函数每个维度分别求极小值，即分别求关于极小值。

然后是最小值和极小值，如果是凸函数，梯度下降会收敛到最小值，因为只有一个极小值，它就是最小值。

至于什么是凸函数，详见我的专栏文章：掌握机器学习数学基础之凸优化。

对于理论支持：

Optimization Methods for Large-Scale Machine Learning：这论文之前的问答也看到了，贴下知友的翻译。为什么我们更宠爱“随机”梯度下降？

ROBUST STOCHASTIC APPROXIMATION APPROACH TO STOCHASTIC PROGRAMMING

An Introduction to optimization

以上三个关于优化的文章，一切问题，自然随之而解。值得一看！

3. 随机梯度下降可视化

作者：量子位
链接：https://www.zhihu.com/question//answer/
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

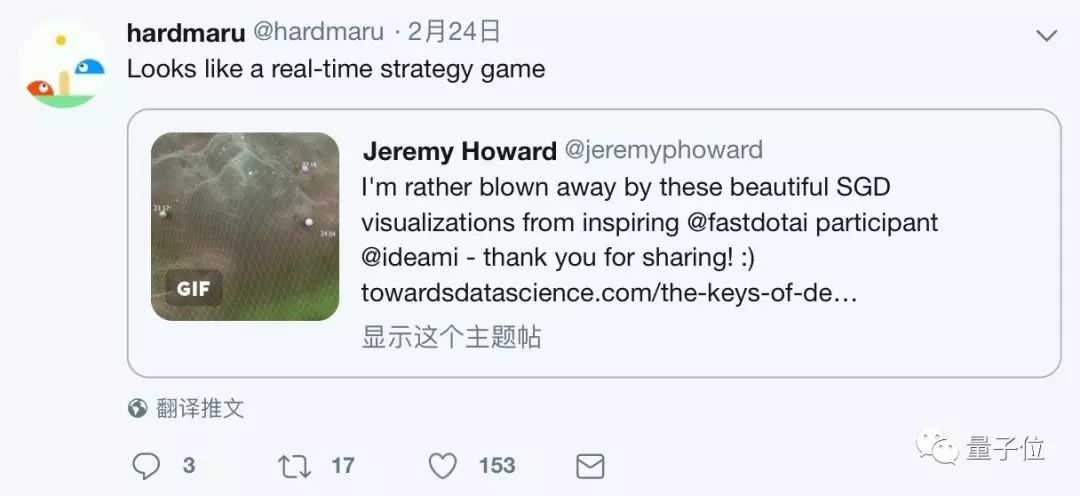
下面的这张动图演示，乍看就像就像是在复杂地形中作战的沙盘推演，其实揭示的是随机梯度下降（SGD）算法的本质。

让小球滚下山坡，找到它们分别落在哪个山谷里，原来梯度下降算法还能变得像游戏视频一样酷炫。

谷歌大脑东京研究员hardmaru转发了视频对应的文章，评价它“像极了即时战略游戏”。

可别光顾着好玩，视频还得配合文章一起“服用”才有效果。上面的热门视频就是摘自fast.ai成员Javier Ideami写的一篇科普文。

如果代码和公式让你感到枯燥，那么不妨从这段酷炫的SGD视频入手，再读一读这篇文章，它会帮你更直观地理解深度学习。

到底什么是梯度？

深度学习的架构和最新发展，包括CNN、RNN、造出无数假脸的GAN，都离不开梯度下降算法。

梯度可以理解成山坡上某一点上升最快的方向，它的反方向就是下降最快的方向。想要以最快的方式下山，就沿着梯度的反方向走。

看起来像沙盘推演的东西，其实是我们撒出的小球，它们会沿着梯度下降的方向滚到谷底。

而梯度下降算法的最终目的，是找到整个“地形”中的最低点（全局最小值），也就是海拔最低的山谷。

但在这片地形中，山谷可能不止一处（局部最小值），所以我们需要撒很多球，让它们分别落入不同山谷，最后对比高度找到其中的海拔最低点。

以上就是随机梯度下降（SGD）算法的基本思想。

今天的文章
深度学习数学基础(二)～随机梯度下降(Stochastic Gradient Descent, SGD)分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/80104.html