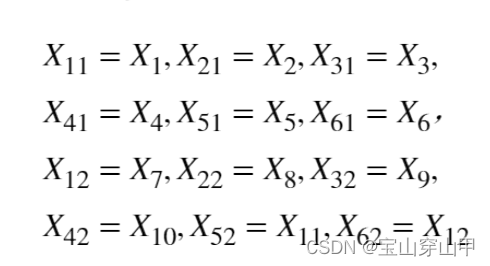数学建模笔记(二)——非线性规划
一、基本介绍
线性规划与非线性规划的差距
线性规划是指模型中所有变量的次数只能是一次,非线性规划就是包含 x a ( a ≠ 1 ) , sin ( x ) , cos ( x ) , e x , l n ( x ) x^a(a\not=1),\sin(x),\cos(x),e^x,ln(x) xa(a=1),sin(x),cos(x),ex,ln(x)的模型。
m i n f ( x ) = x 1 2 + x 2 2 + x 3 2 + 8 { x 1 2 − x 2 + x 3 2 ≥ 0 x 1 + x 2 2 + x 3 3 ≤ 20 − x 1 − x 2 2 + 2 = 0 x 2 + 2 x 3 2 = 3 x 1 , x 2 , x 3 ≥ 0 minf(x)=x_1^2+x_2^2+x_3^2+8\\ \begin{cases} x_1^2-x_2+x_3^2\ge0\\ x_1+x_2^2+x_3^3\le20\\ -x_1-x_2^2+2=0\\ x_2+2x_3^2=3\\ x_1,x_2,x_3\ge0 \end{cases} minf(x)=x12+x22+x32+8⎩
⎨
⎧x12−x2+x32≥0x1+x22+x33≤20−x1−x22+2=0x2+2x32=3x1,x2,x3≥0
在形式上和线性规划相当类似,解题步骤上也是类似,先确定决策变量,再写出目标函数和约束条件。
模型简介
虽然形式上与线性规划相当类似,但是求解却相当复杂。
-
因为线性规划有通用的求准确解的方法,一定可以求到最优解:happy:
-
非线性规划在数学上并没有求的精准数值解的通用方法
-
可也通过matlab的fmincon函数求的近似解
非线性规划的解可以存在在可行域上的任意一点
二、求解方法
f m i n c o n fmincon fmincon方法
m a t l a b matlab matlab的 f m i n c o n fmincon fmincon函数可以求解: [ x , f v a l ] = f m i n c o n ( f u n , x 0 , A , b , A e q , b e q , l b , u b , n o n l c o n ) [x,fval]=fmincon(fun,x_0,A,b,Aeq,beq,lb,ub,nonlcon) [x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
注意初始值 x 0 x_0 x0会影响求解结果,可以多次设不同的初始值进行比较,或者配合蒙特卡洛法进行求解。
| f u n fun fun | 单独定义在脚本文件里的目标函数 |
|---|---|
| x 0 x_0 x0 | 决策变量的初始值( 影响最终结果 \textcolor{red}{影响最终结果} 影响最终结果) |
| A , b A,b A,b | 线性约束不等式变量的系数矩阵和常数项矩阵 |
| A e q , b e q Aeq,beq Aeq,beq | 线性约束灯饰变量的系数矩阵和常数项举证 |
| l b , u b lb,ub lb,ub | 决策变量的最小值和最大值 |
| n o n l c o n nonlcon nonlcon | 非线性约束,包括等式和不等式 |
S c i p y . o p t i m i z e Scipy.optimize Scipy.optimize模块
除了 m a t l a b 的 f m i n c o n matlab的fmincon matlab的fmincon可以进行求解以外,我们通常还可以使用python的库 S c i p y Scipy Scipy的 O p t i m i z e Optimize Optimize模块来进行求解。
s c i p y . o p t i m i z e scipy.optimize scipy.optimize提供了多个用于非线性规划的方法:
- b r e n t ( ) brent() brent():单变量无约束优化问题,用的是牛顿法/二分法。
- f m i n ( ) fmin() fmin():多变量无约束优化问题,使用单纯形法,只需要利用函数值,不用函数的导数。
- l e a t s q ( ) leatsq() leatsq():非线性最小二乘拟合问题
- m i n i m i z e ( ) minimize() minimize():约束优化问题,通过拉格朗日乘子法将约束问题转化成无约束问题
三、例题讲解
m a t l a b matlab matlab例题
1.工地选址
某公司有6个建筑工地要开工,每个工地的位置(用平面坐标系a,b表示,距离单位:km) 及水泥日用量d(单位:t)由下表给出。目前有两个临时料场位于A(5,1),B(2,7)。 日储量各有== 20 t 20t 20t==。假设从料场到工地之间均有直线道路相连。
- 问题一:试制定每天的供应计划,即从A,B两料场分别向各工地运送多少吨水泥,使总的吨千米数最小?
- 问题二:为了进一步减少吨千米数,打算舍弃这两个临时料场,改建两个新的,日储量各为 20 t 20t 20t。问应建在何处,节省的吨千米数为多大?
| 工地 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| a | 1.25 | 8.75 | 0.5 | 5.75 | 3 | 7.25 |
| b | 1.25 | 0.75 | 4.75 | 5 | 6.5 | 7.75 |
| d | 3 | 5 | 4 | 7 | 6 | 11 |
1、确定决策变量
- 第 i i i个工地的坐标为 ( a i , b i ) (a_i,b_i) (ai,bi),水泥的日用量为 d i , i = 1 , 2 , 3 … 6 d_i,i=1,2,3\dots 6 di,i=1,2,3…6;料场位置 ( x j , y j ) (x_j,y_j) (xj,yj),日储量为 e j , j = 1 , 2 e_j,j=1,2 ej,j=1,2,从料场 j j j运往工地 i i i的运送量为 X i j X_{ij} Xij。
- 第一问中已确定料场的位置,所以距离已知质量,因此该题为线性规划问题,第二问则为非线性规划问题。
- 第一问决策变量为 X i j X_{ij} Xij,第二问的决策变量为 x j , y j , X i j x_j,y_j,X_{ij} xj,yj,Xij。
2、确定约束条件
每日的水泥用料量不能超过最大限额:
∑ i = 1 6 X i j ≤ e j , j = 1 , 2 \sum_{i=1}^6X_{ij}\le e_j,j=1,2 i=1∑6Xij≤ej,j=1,2
每个工地的水泥量必须等于要求量:
∑ j = 1 2 X i j = d i , i = 1 , 2 … 6 \sum_{j=1}^2X_{ij}=d_i,i=1,2\dots 6 j=1∑2Xij=di,i=1,2…6
3、确定目标函数
要求总千米吨数最小,即运送量乘以运送里程的求和:
∑ i = 1 6 ∑ i = 1 2 X i j ( x j − a i ) 2 + ( y j − b i ) 2 , i = 1 , 2 … 6 , j = 1 , 2 \sum_{i=1}^6\sum_{i=1}^2X_{ij}\sqrt{(x_j-a_i)^2+(y_j-b_i)^2},i=1,2\dots6,j=1,2 i=1∑6i=1∑2Xij(xj−ai)2+(yj−bi)2,i=1,2…6,j=1,2
连立,可得模型
m i n f = ∑ i = 1 6 ∑ i = 1 2 X i j ( x j − a i ) 2 + ( y j − b i ) 2 s . t . { ∑ i = 1 6 X i j ≤ e j , j = 1 , 2 ∑ j = 1 2 X i j = d i , i = 1 , 2 … 6 minf=\sum_{i=1}^6\sum_{i=1}^2X_{ij}\sqrt{(x_j-a_i)^2+(y_j-b_i)^2}\\ s.t.\begin{cases}\sum_{i=1}^6X_{ij}\le e_j,j=1,2\\ \sum_{j=1}^2X_{ij}=d_i,i=1,2\dots 6 \end{cases} minf=i=1∑6i=1∑2Xij(xj−ai)2+(yj−bi)2s.t.{
∑i=16Xij≤ej,j=1,2∑j=12Xij=di,i=1,2…6
- 对于第一题,只有一个决策变量 X i j X_{ij} Xij,目标函数中根号下的 x j x_j xj和 y j y_j yj是常数,目标函数和约束条件都是线性的,所以第一题是求解线性规划问题。
- 对于第二题,因为存在 ( x j − a i ) 2 + ( y j − b i ) 2 \sqrt{(x_j-a_i)^2+(y_j-b_i)^2} (xj−ai)2+(yj−bi)2,所以是非线性的
.
4,代码
clear;clc;
% 6个工地坐标 数据初始化
a=[1.25 8.75 0.5 5.75 3 7.25];
b=[1.25 0.75 4.75 5 6.5 7.75];
% 临时料场位置
x=[5 2];
y=[1 7];
% 6个工地水泥日用量
d=[3 5 4 7 6 11];
% 计算目标函数系数,即6工地与两个料场的距离,总共12个值
for i=1:6 % 对于6个工地
for j=1:2 % 接收两个料场的供用
l(i,j)=sqrt((x(j)-a(i))^2+(y(j)-b(i))^2); % 距离
end
end
%第一题的求解
f = [l(:,1);l(:,2)]; % 目标函数系数向量,总共12个值
% 不等式约束条件的变量系数和常数项
A = [1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1];
% 两个临时料场日储量
b = [20;20];
% 矩阵的行数是约束条件个数,列数是变量个数
% 等式约束的变量系数和常数项
Aeq = [eye(6),eye(6)]; % 两个单位矩阵横向拼成
beq=[d(1);d(2);d(3);d(4);d(5);d(6)];
% 所有变量下限全是0
Vlb=[0 0 0 0 0 0 0 0 0 0 0 0];
[x,fval]=linprog(f,A,b,Aeq,beq,Vlb);
x,fval
延续第一问设的 X 1 X_1 X1到 X 12 X_{12} X12,代表料场到工地的运输水泥量;
第二问要求确定新料场的位置,所以要再添加4个变量,作为两个新料场的横纵坐标。
因此,第二问有16个变量,设定为 X 1 X_1 X1到 X 16 X_{16} X16。
相应地,每个约束条件的系数矩阵中,也要有16个元素。
% 第二问中求新料场位置,所以两个料场的横纵坐标也是变量,所以多了4个变量
% 对新坐标没有不等式约束,所以其不等式约束条件里的系数为0
A2 = [1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0];
B2 = [20;20];
% 对新坐标也没有等式约束,所以相应项也为0
Aeq2 = [eye(6),eye(6),zeros(6,4)]; % 两个单位矩阵和一个全0矩阵拼成
beq2=[3 5 4 7 6 11]';
Vlb2=[zeros(12,1);-inf;-inf;-inf;-inf];
m a t l a b 的 f m i n c o n matlab的fmincon matlab的fmincon必须赋初值,可以直接用第一问的结果作为初始值。
x0=[3 5 0 7 0 1 0 0 4 0 6 10 5 1 2 7]';
[x2,fval2]=fmincon(@obj_f,x0,A2,B2,Aeq2,beq2,Vlb2)
本题只有目标函数有非线性函数,若约束条件中有非线性函数,可以使用nonlcon项,具体可以参考
https://ww2.mathworks.cn/help/optim/ug/fmincon.html?searchHighlight=fmincon&s_tid=srchtitle_fmincon_1#busog7r-nonlcon
若有条件,可使用蒙特卡罗法求一个近似解作为初始值
1、因为第2问模型中有16个变量,所以要给16个变量分别生成随机值,作为当前解;
2、判断这些当前解是否满足模型的约束条件
3、若满足,代入目标函数,求当前目标函数值
4、判断当前目标函数值是否比已求的较优函数值更好,若是,则替换掉较优函数值和对应的较优解
5、不断重复前5步,构成统计意义,求得较优解。
python例题
1, b r e n t brent brent
例,求出函数 f ( x ) = x 2 + 8 s i n ( 2 x + π ) f(x)=x^2+8sin(2x+\pi) f(x)=x2+8sin(2x+π)的最大值。
scipy.optimize.brent(func, args=(), brack=None, tol=1.48e-08, full_output=0, maxiter=500)
o p t i m i z e . b r e n t ( ) optimize.brent() optimize.brent()的主要参数
| f u n c : c a l l a b l e f ( x , ∗ a r g s ) func:callable f(x,*args) func:callablef(x,∗args) | 目标函数,以函数形式表示,可通过 ∗ a r g s *args ∗args传递参数 |
|---|---|
| a r g s args args:tuple | 可选项 |
| b r a c k : t u p l e brack:tuple brack:tuple | 可选项,搜索算法的开始区间(并不是x的上下限) |
o p t i m i z e . b r e n t ( ) optimize.brent() optimize.brent()的主要参数
| x m i n : xmin: xmin: | 返回函数达到最小值时的x |
|---|---|
| f v a l : fval: fval: | 返回函数的最优值 |
代码如下
from scipy.optimize import brent, fmin_ncg, minimize
import numpy as np
# 1. Demo1:单变量无约束优化问题(Scipy.optimize.brent)
def objf(x): # 目标函数
fx = x**2 - 8*np.sin(2*x+np.pi)
return fx
xIni = -5.0
xOpt= brent(objf, brack=(xIni,2))
print("xIni={:.4f}\tfxIni={:.4f}".format(xIni,objf(xIni))
print("xOpt={:.4f}\tfxOpt={:.4f}".format(xOpt,objf(xOpt)))
最后求得结果为
x I n i = − 5.0000 , f x I n i = 29.3522 x O p t = − 0.7391 , f x O p t = − 7.4195 xIni=-5.0000 ,fxIni=29.3522\\ xOpt=-0.7391 ,fxOpt=-7.4195 xIni=−5.0000,fxIni=29.3522xOpt=−0.7391,fxOpt=−7.4195
2, f m i n fmin fmin
多变量无约束优化问题的算法很多,分类方式也很多。从使用者的角度来说可以分为:只使用目标函数值、使用导数(梯度下降法)、使用二阶导数。大体来说,使用导数的算法收敛较快,使用二阶导数收敛更快,但是收敛快也容易陷入局部最优。
f m i n ( ) fmin() fmin() 函数是 SciPy.optimize 模块中求解多变量无约束优化问题(最小值)的首选方法,采用下山单纯性方法。下山单纯性方法又称 Nelder-Mead 法,只使用目标函数值,不需要导数或二阶导数值,是最重要的多维无约束优化问题数值方法之一。
scipy.optimize.fmin(func, x0, args=(), xtol=0.0001, ftol=0.0001, maxiter=None, maxfun=None, full_output=0, disp=1, retall=0, callback=None, initial_simplex=None)
案例:
这题是一个经典函数,用来测试优化算法性能的非凸函数。叫 R o s e n b r o c k Rosenbrock Rosenbrock山谷函数
f ( x , y ) = ( 1 − x ) 2 + 100 ( y − x 2 ) 2 f(x,y)=(1-x)^2+100(y-x^2)^2 f(x,y)=(1−x)2+100(y−x2)2
代码中通过一个二元列表代替了x和y两个变量。
from scipy.optimize import brent, fmin, minimize
import numpy as np
# 2. Demo2:多变量无约束优化问题(Scipy.optimize.brent)
# Rosenbrock 测试函数
def objf2(x): # Rosenbrock benchmark function
fx = sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)
return fx
xIni = np.array([-2, -2])
xOpt = fmin(objf2, xIni)
print("xIni={:.4f},{:.4f}\tfxIni={:.4f}".format(xIni[0],xIni[1],objf2(xIni)))
print("xOpt={:.4f},{:.4f}\tfxOpt={:.4f}".format(xOpt[0],xOpt[1],objf2(xOpt)))
今天的文章数学建模中非线性规划_线性规划数学建模案例分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/80753.html