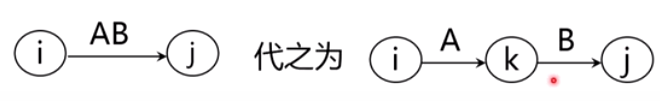编译原理学习笔记6——DFA和NFA
6.1 有限自动机的等价性
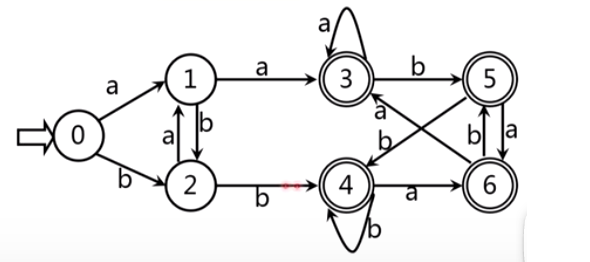
6.1.1 NFA转换成DFA
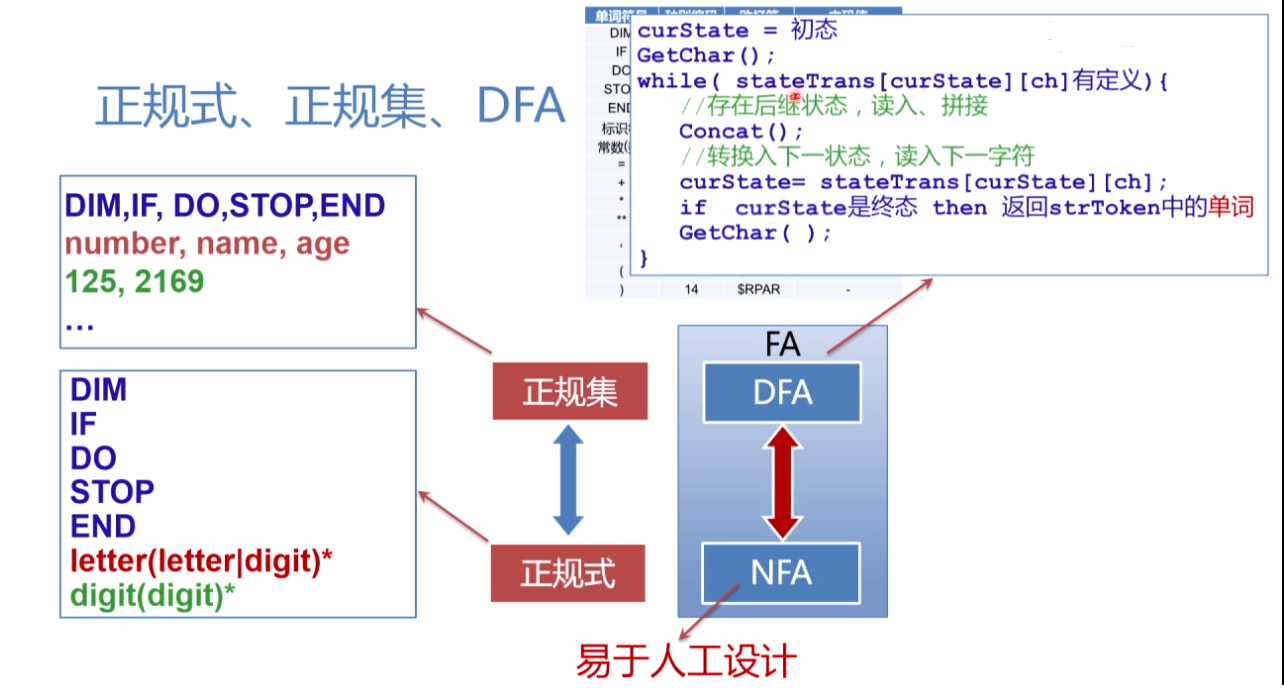
DFA (Deterministic finite automata, 确定的有穷自动机)是NFA(Nondeterministic finite automata, 非确定的有穷自动机)的特例。
- 对于每个NFA M存在一个DFA M’,使得L(M)=L(M’)
- 等价性证明
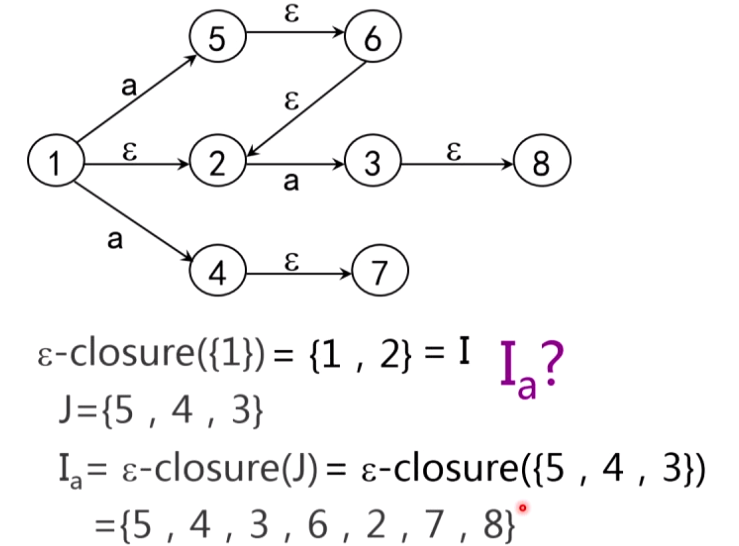
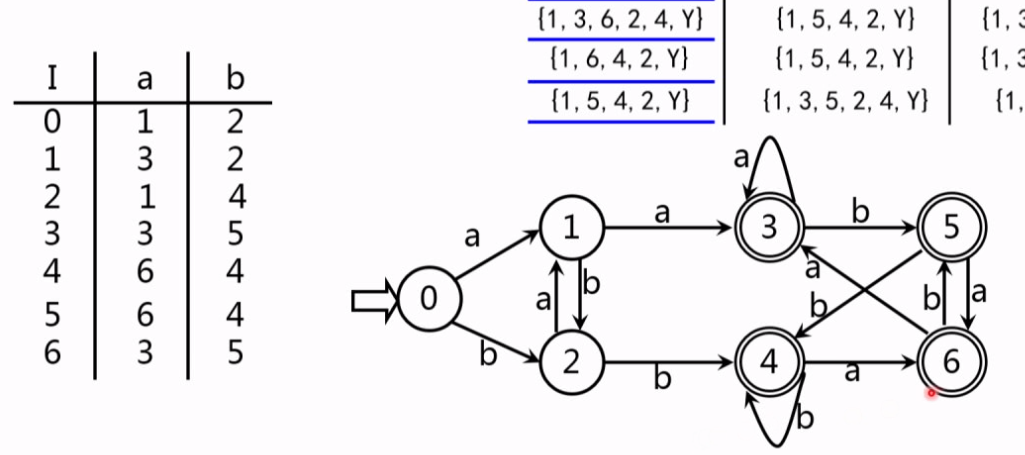
- NFA的确定化
转换:
6.1.2 DFA的化简——状态的等价性
- DFA的化简(最小化)
- 对于给定的DFA M,寻找一个状态数比M少的DFAM’‘,使得L(M)=L(M’)
- 状态的等价性
- 假设s和t为M的两个状态,称s和 t 等价∶如果从状态s出发能读出某个字α而停止于终态,那么同样,从t出发也能读出α而停止于终态;反之亦然。
- 两个状态不等价,则称它们是可区别的。
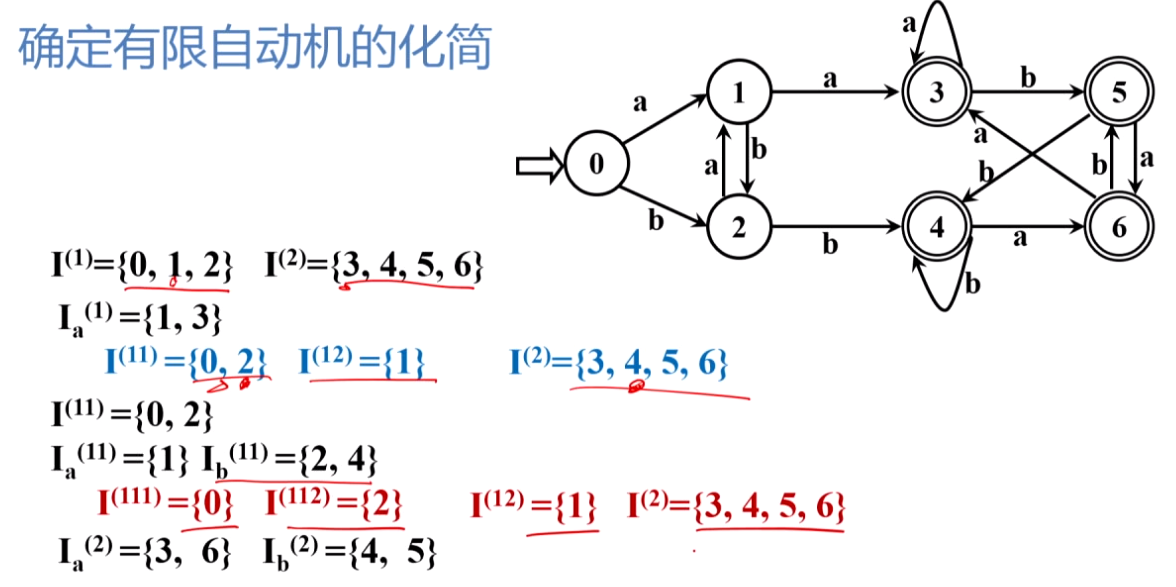
确定有限自动机的化简
基本思想
- 把M的状态集划分为一些不相交的子集,使得任何两个不同子集的状态是可区别的,而同一子集的任何两个状态是等价的。
- 最后,让每个子集选出一个代表,同时消去其他状态。
按照上述原则对DFA的状态集合S进行第一次划分,正确的分法是()
- A.初态和非初态
- B.终态和非终态
- C.初态、终态、其他状态
答案:B
- 把状态集划分为一些不相交的子集,使得任何两个不同子集的状态是可区别的,而同一子集的任何两个状态是等价的。
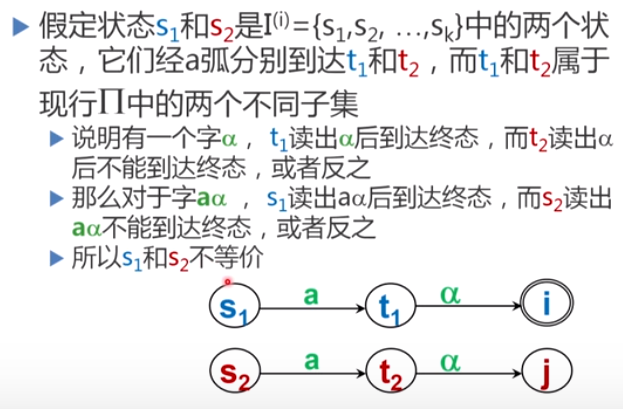
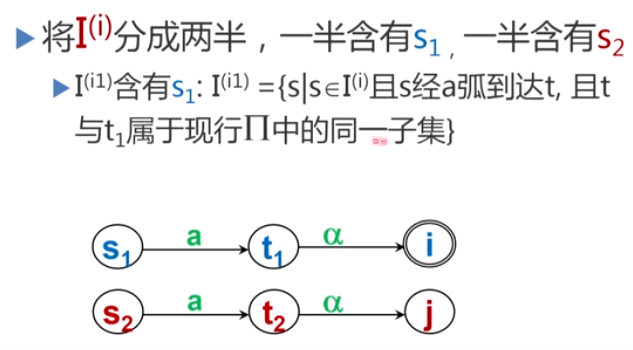
- 可区别:存在一个字α,要么s读出α停止于终态而t读出α停止于非终态,要么t读出α停止于终态而s读出α停止于非终态
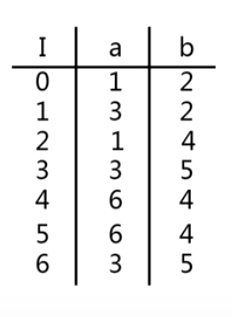
6.1.3 DFA的化简——化简算法
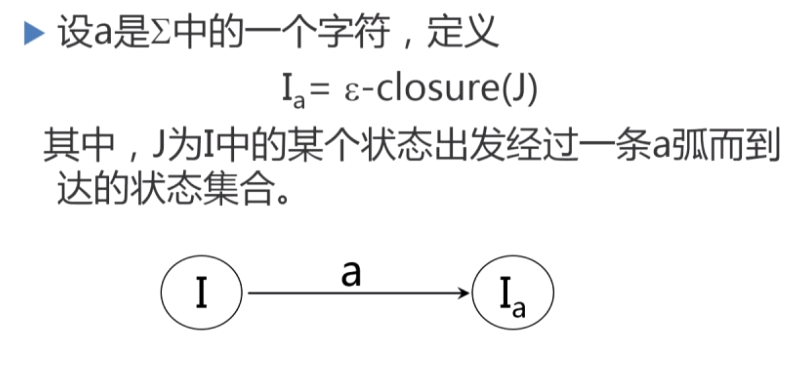
- 一般地,对某个a和I(i),若I(i)落入现行П中N个不同子集,则应把I(i)划分成N个不相交的组,使得每个组J的Ja都落入的Пl同一子集。
- 重复上述过程,直到Пl所含子集数不再增长。
- 对于上述最后划分П中的每个子集,我们选取每个子集中的一个状态代表其他状态,则可得到化简后的DFA M’
- 若某子集含有原来的初态,则其代表为新的初态,若某子集含有原来的终态,则其代表为新的终态。
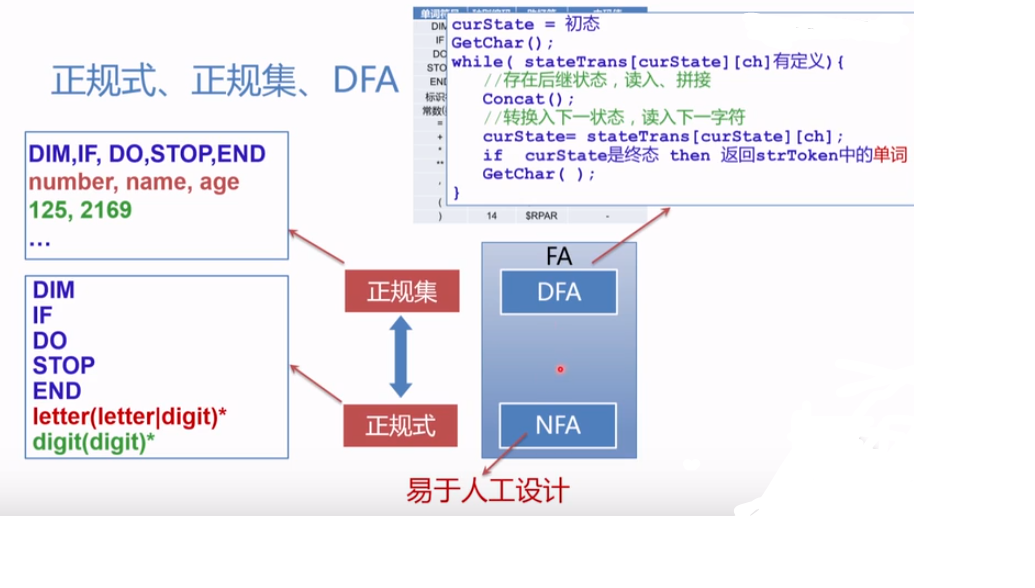
6.2 正规式与有限自动机的等价性
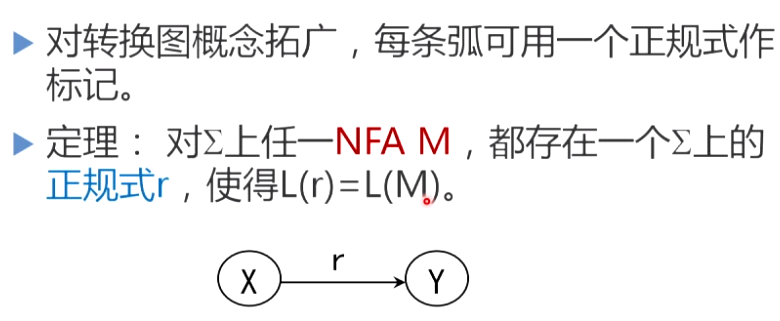
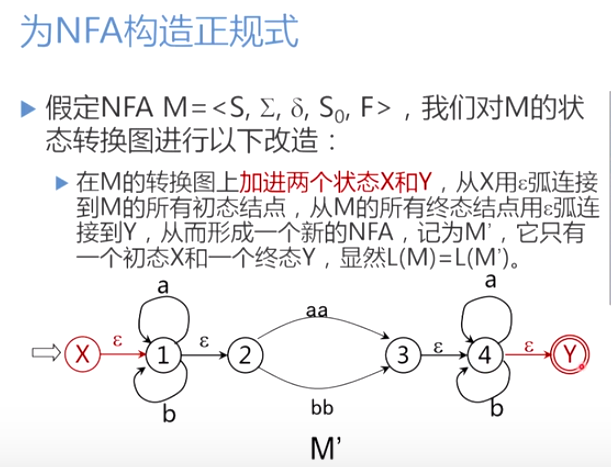
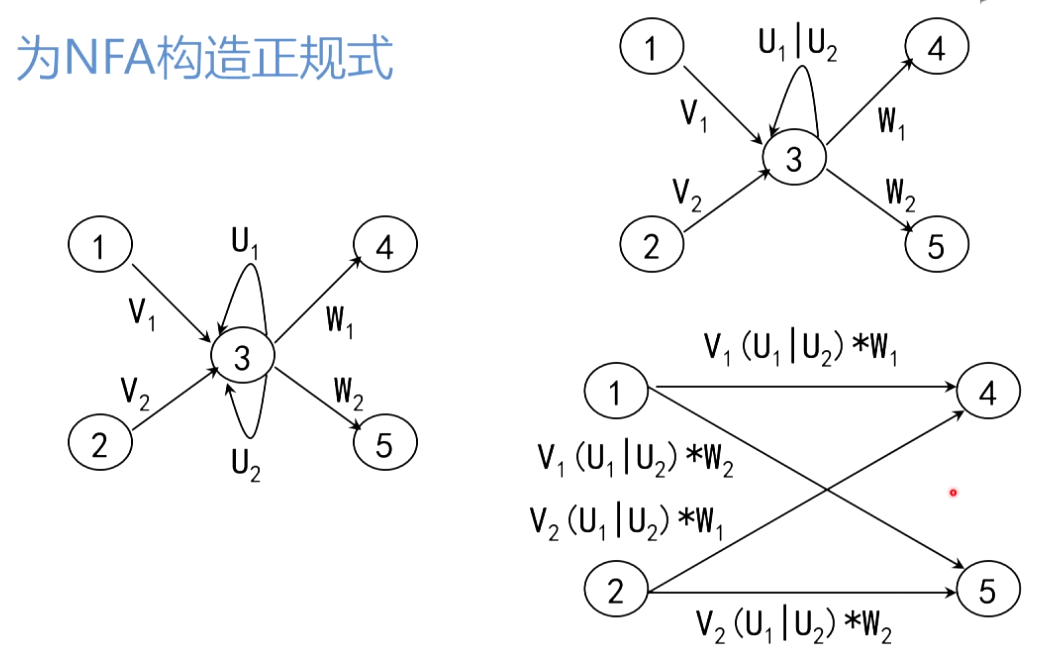
6.2.1 为NFA构造正规式
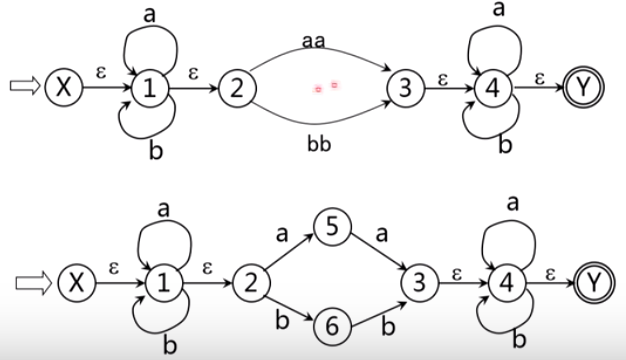
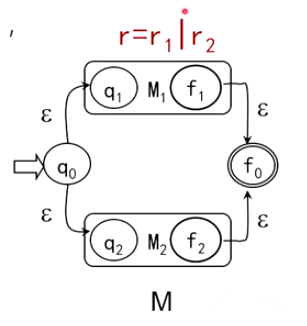
6.2.2 为正规式构造NFA——数学归纳法证明
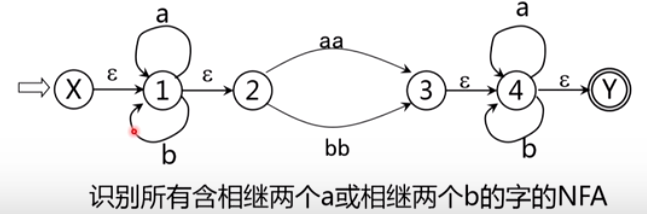
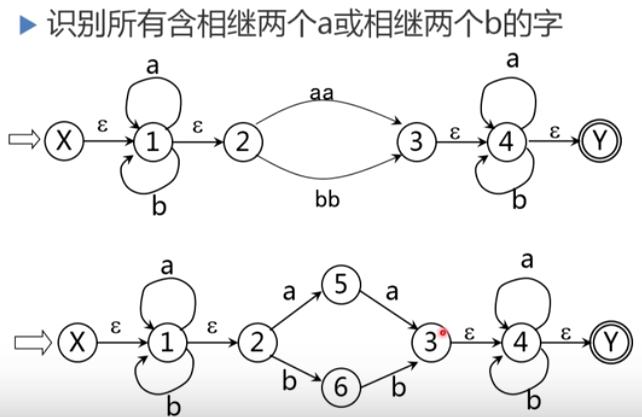
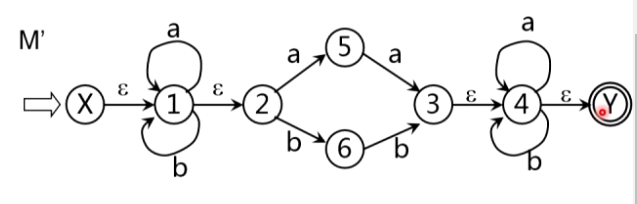
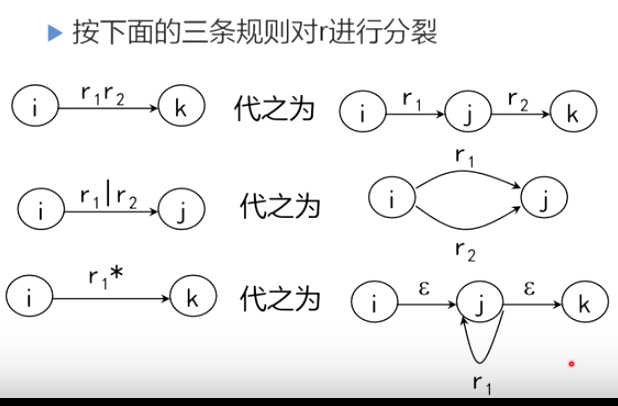
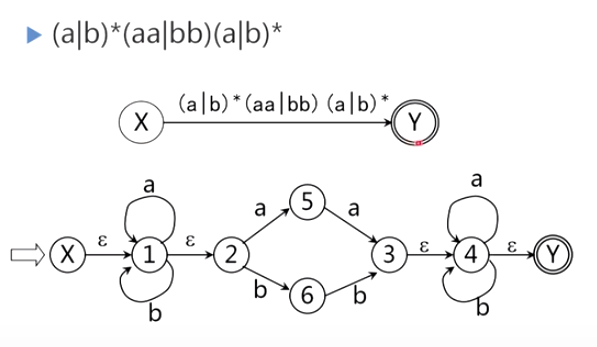
6.2.3 为正规是构造NFA——算法及示例
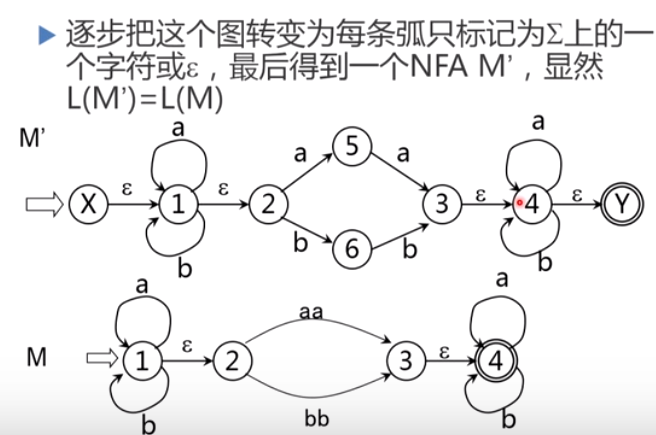
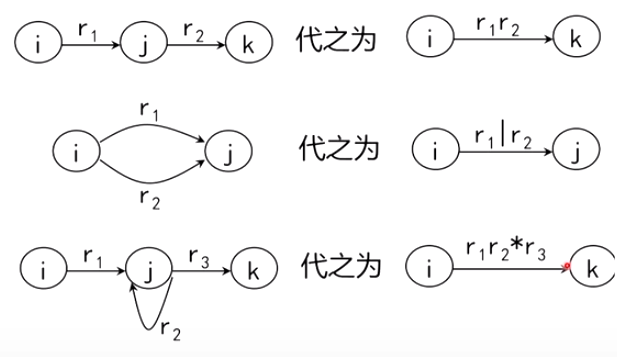
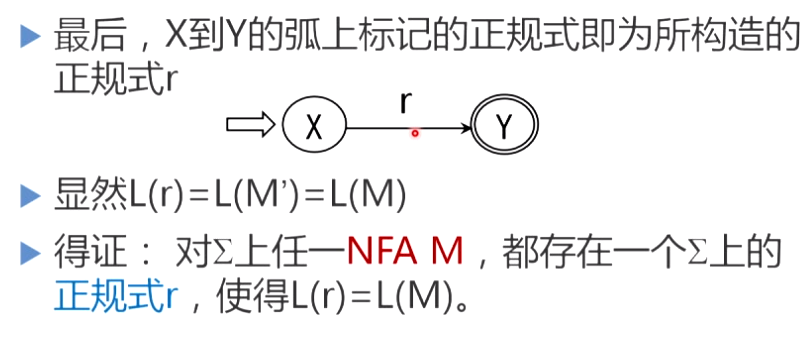
逐步把这个图转变为每条弧只标记为E上的一个字符或,最后得到一个NFAM’,显然L(M’)=L®
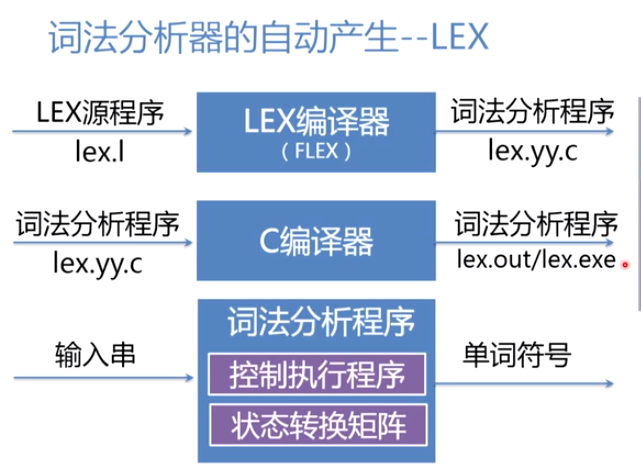
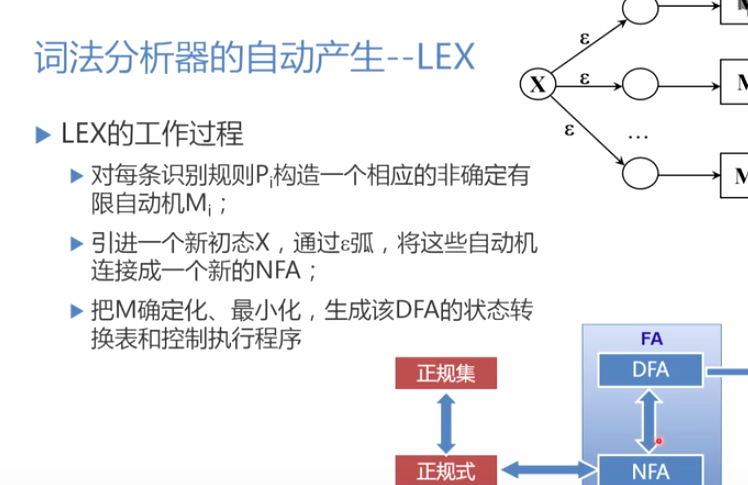
6.3 词法分析程序自动生成——LEX
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/80806.html