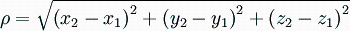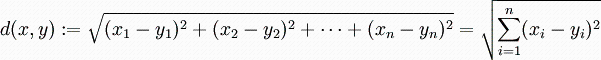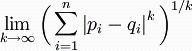欧几里得距离和曼哈顿距离都满足的数学性质有_两点间的欧式距离怎么算

1.欧几里得距离（欧式距离）

它是在m维空间中两个点之间的真实距离。在二维和三维空间中的欧氏距离的就是两点之间的距离（简单来说就是两点之间直线最短的那段距离）。相关联的范数称为欧几里得范数，也称 $L_2$ 范数。

二维空间的公式

三维空间的公式

n维空间的公式

2.曼哈顿距离

曼哈顿距离也称出租车几何，是由十九世纪的赫尔曼·闵可夫斯基在曼哈顿街区研究时所创词汇，是种使用在几何度量空间的几何学用语，用以标明 两个点在标准坐标系上的绝对轴距总和。

例如在平面上，坐标 $(X_1,Y_1)$ 的点与坐标 $(X_2,Y_2)$ 的点的曼哈顿距离为：
$$S=|X_1-X_2|+|Y_1-Y_2|$$

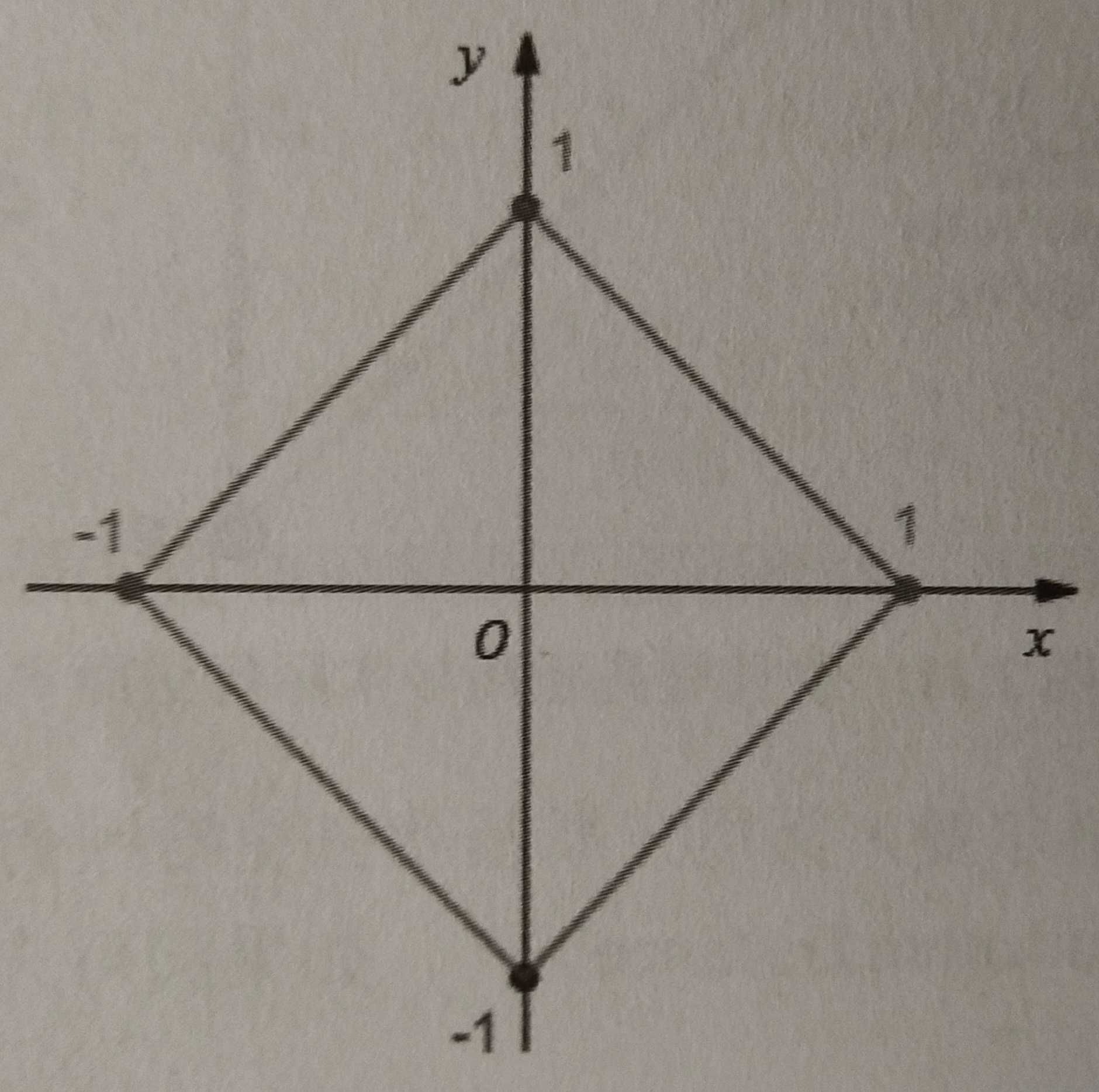
图中两点间的绿线代表的是 欧式距离 。红线，蓝线和黄线代表的都是 曼哈顿距离，由此可见在两点间曼哈顿距离相等的情况下，线路有多种情况。

到原点的曼哈顿距离为 1 的所有点可以构成一个边长为 $\sqrt{2}$ 的正方形

3.切比雪夫距离

切比雪夫距离或是 $L_{\infty }$ (无穷范数) 度量是向量空间中的一种度量，二个点之间的距离定义为其各座标数值差的最大值。

若二个向量或二个点p、q，其座标分别为 $p_i$ 及 $q_i$，则两者之间的切比雪夫距离定义如下：

这也等于以下 $L_p$ 度量的极值：

因此切比雪夫距离也称为 $L_{\infty }$ 度量（无穷范数）

以 $(x_1,y_1)$ 和 $(x_2,y_2)$ 二点为例，其切比雪夫距离为:
$$S=max\left(\left|x_2-x_1\right|,\left|y_2-y_1\right|\right)$$

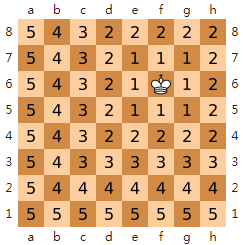
国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格，因此可以较有效率的到达目的的格子。上图是棋盘上所有位置距 f6 位置的切比雪夫距离。

今天的文章欧几里得距离和曼哈顿距离都满足的数学性质有_两点间的欧式距离怎么算分享到此就结束了，感谢您的阅读。