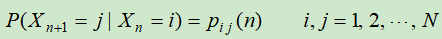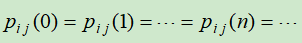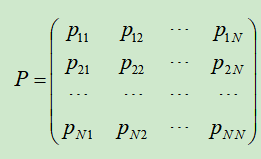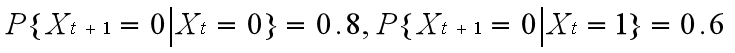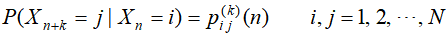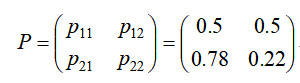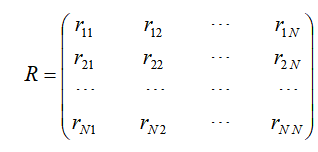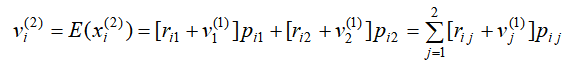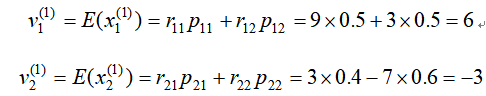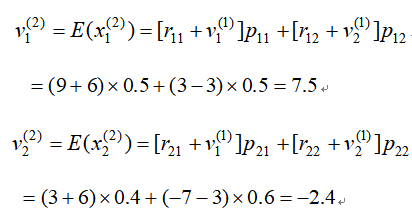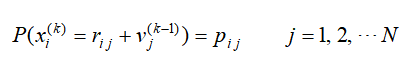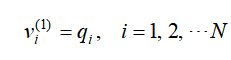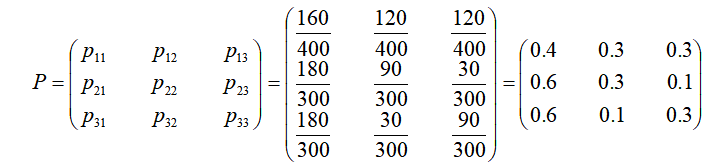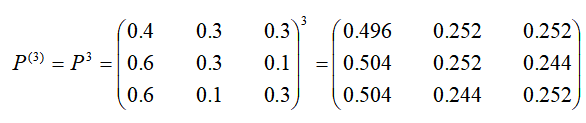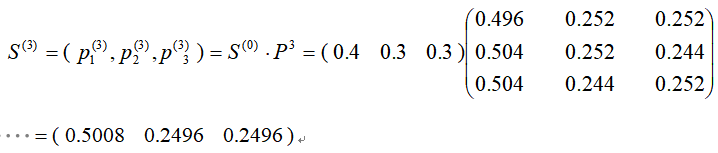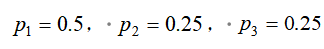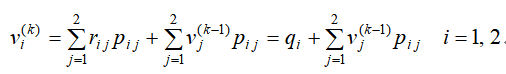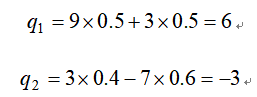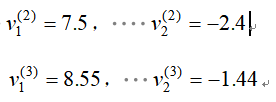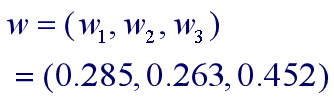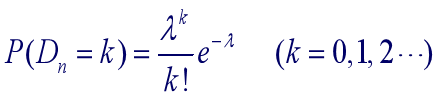马尔可夫链模型步骤_简单线性模型的高斯马可夫定理

要描述某种特定时期的随机现象如某种药品在未来某时期的销售情况，比如说第n季度是畅销还是滞销，用一个随机变量Xn便可以了，但要描述未来所有时期的情况，则需要一系列的随机变量X1，X2，…，Xn，…．称{
Xt，t∈T ，T是参数集}为随机过程，{
Xt }的取值集合称为状态空间。若随机过程{
Xn }的参数为非负整数， Xn 为离散随机变量，且{
Xn }具有无后效性（或称马尔可夫性），则称这一随机过程为马尔可夫链（简称马氏链）。所谓无后效性，直观地说，就是如果把{
Xn }的参数n看作时间的话，那么它在将来取什么值只与它现在的取值有关，而与过去取什么值无关。

马氏链模型说明

时间、状态均为离散的随机转移过程
系统在每个时期所处的状态是随机的
从一时期到下时期的状态按一定概率转移
下时期状态只取决于本时期状态和转移概率
已知现在，将来与过去无关（无后效性）

转移概率矩阵

对具有N个状态的马氏链，描述它的概率性质，最重要的是它在n时刻处于状态i下一时刻转移到状态j的一步转移概率：

若假定上式与n无关，即

则可记为 $p_{ij}$ （此时，称过程是平稳的），并记

称为转移概率矩阵。

转移概率矩阵性质

转移概率矩阵具有下述性质：

气象案例的马尔可夫链表示

由于第二天天气情况不受今天之前天气情况的影响，即状态0和状态1是相互独立且仅有的状态，所以两个状态的概率和为1。因此，该随机过程具有马尔可夫属性，该过程称为马尔可夫链。

因此，转移矩阵为：

k步转移概率矩阵

如果我们考虑状态多次转移的情况，则有过程在n时刻处于状态i，n+k时刻转移到状态j的k步转移概率：

同样由平稳性，上式概率与n无关，可写成 $p_{ij}^{(k)}$ 。记

称为k步转移概率矩阵．其中具有性质：

一般地有，若P为一步转移矩阵，则k步转移矩阵

气象案例的k步转移矩阵

2步转移矩阵：

说明：该2步矩阵说明，如果今天是晴天（0），那么后两天仍为晴天（0）的概率为0.76，为雨天（1）概率是0.24；类似地，如果今天是雨天（1），那么后两天为晴天（0）的概率是0.72，为雨天（1）的概率为0.28。

同样，3天、4天或5天后的气象状态转移概率可通过计算3步、4步和5步转移矩阵得到：

状态转移概率

在马尔可夫预测方法中，系统状态的转移概率的估算非常重要．估算的方法通常有两种：一是主观概率法，它是根据人们长期积累的经验以及对预测事件的了解，对事件发生的可能性大小的一种主观估计，这种方法一般是在缺乏历史统计资料或资料不全的情况下使用．二是统计估算法，现通过实例进行介绍。

实例：求销售状态的转移概率矩阵

记录了某抗病毒药的6年24个季度的销售情况，得到表1．试求其销售状态的转移概率矩阵．

表1 某抗病毒药24个季度的销售情况

季度	销售状态	季度	销售状态	季度	销售状态	季度	销售状态
1	1 (畅销)	7	1(畅销)	13	1(畅销)	19	2(滞销)
2	1(畅销)	8	1(畅销)	14	1(畅销)	20	1(畅销)
3	2(滞销)	9	1(畅销)	15	2(滞销)	21	2(滞销)
4	1(畅销)	10	2(滞销)	16	2(滞销)	22	1(畅销)
5	2(滞销)	11	1(畅销)	17	1(畅销)	23	1(畅销)
6	2(滞销)	12	2(滞销)	18	1(畅销)	24	1(畅销)

分析表中的数据，其中有15个季度畅销，9个季度滞销，连续出现畅销和由畅销转入滞销以及由滞销转入畅销的次数均为7，连续滞销的次数为2．由此，可得到下面的市场状态转移情况表（表2）．

表2 市场状态转移情况表

		下季度药品所处的市场状态
		1（畅销）	2（滞销）
				本季度药品所	1（畅销）	7	7
处的市场状态	2（滞销）	7	2

现计算转移概率．以频率代替概率，可得连续畅销的概率：

分母中的数为15减1是因为第24季度是畅销，无后续记录，需减1．

同样得由畅销转入滞销的概率：

滞销转入畅销的概率：

连续滞销的概率：

综上，得销售状态转移概率矩阵为：

从上面的计算过程知，所求转移概率矩阵P的元素其实可以直接通过表2中的数字计算而得到，即将表中数分别除以该数所在行的数字和便可：

由此，推广到一般情况，我们得到估计转移概率的方法：假定系统有m种状态S1，S2，…，Sm，根据系统的状态转移的历史记录，得到表3的统计表格，以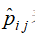表示系统从状态i转移到状态j的转移概率估计值，则由表3的数据计算估计值的公式如下：

表3 系统状态转移情况表

		系统下步所处状态
		$S_{1}$	$S_{2}$	…	$S_{m}$
		$S_{1}$	$S_{2}$	…	$S_{m}$	系统	$S_{1}$	$n_{11}$	$n_{12}$	…	$n_{1m}$
本步	$S_{2}$	$n_{21}$	$n_{22}$	…	$n_{2m}$
所处		…		…
状态	$S_{m}$	$n_{m1}$	$n_{m2}$	…	$n_{mm}$

Matlab程序

format rat
clc
a=[ 1 1 2 1 2 2 1 1 1 2 1 2,1 1 2 2 1 1 2 1 2 1 1 1];
for i=1:2
for j=1:2
f(i,j)=length(findstr([i j],a));
end
end
f
ni=(sum(f'))'
for i=1:2
p(i,:)=f(i,:)/ni(i);
end
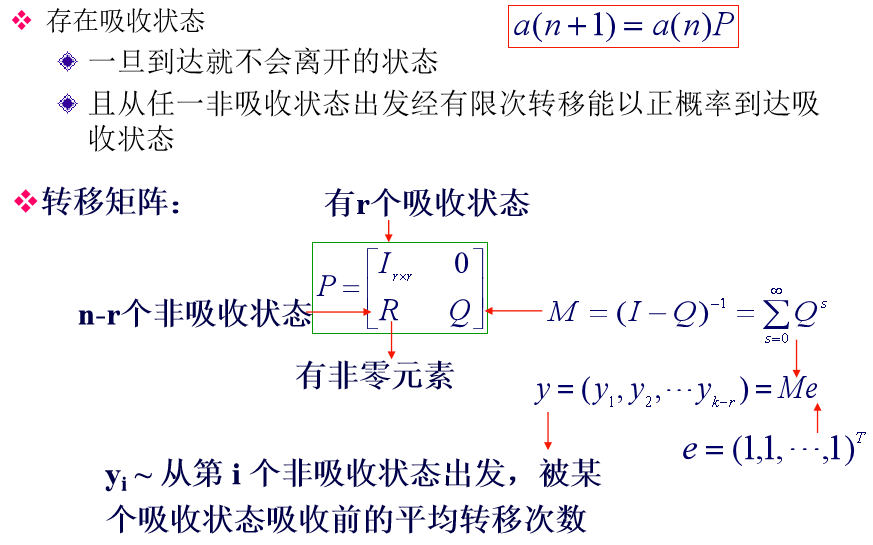
p

正则链

吸收链

马氏链的基本方程

带利润的马氏链

在马氏链模型中，随着时间的推移，系统的状态可能发生转移，这种转移常常会引起某种经济指标的变化．如抗病毒药的销售状态有畅销和滞销两种，在时间变化过程中，有时呈连续畅销或连续滞销，有时由畅销转为滞销或由滞销转为畅销，每次转移不是盈利就是亏本．假定连续畅销时盈r11元，连续滞销时亏本r22元，由畅销转为滞销盈利r12元，由滞销转为畅销盈利r21元，这种随着系统的状态转移，赋予一定利润的马氏链，称为有利润的马氏链．对于一般的具有转移矩阵

的马氏链，当系统由i转移到j时，赋予利润rij（i，j=1，2，…，N），则称

为系统的利润矩阵，rij ＞0称为盈利，rij ＜0称为亏本，rij = 0称为不亏不盈．

随着时间的变化，系统的状态不断地转移，从而可得到一系列利润，由于状态的转移是随机的，因而一系列的利润是随机变量，其概率关系由马氏链的转移概率决定．例如从抗病毒药的销售状态的转移矩阵，得到一步利润随机变量的概率分布分别为：

其中 p11+ p12 = 1 ，p21+ p22 = 1．

如果药品处于畅销阶段，即销售状态为i =1，我们想知道，经过n个季度以后，期望获得的利润是多少？为此，引入一些计算公式．

首先，定义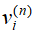为抗病毒药现在处于i(i=1,2)，经过k步转移之后的总期望利润，则

一步转移的期望利润为：

二步转移的期望利润为：

其中随机变量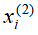（称为二步利润随机变量）的分布为：

例如，若

则抗病毒药销售的一步利润随机变量：

抗病毒药畅销和滞销时的一步转移的期望利润分别为：

二步利润随机变量为：

抗病毒药畅销和滞销时的二步转移的期望利润分别为：

一般地定义k步转移利润随机变量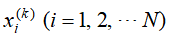的分布为：

则系统处于状态i经过k步转移后所得的期望利润的递推计算式为：

当k=1时，规定边界条件．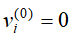

称一步转移的期望利润为即时的期望利润，并记

应用题型一：市场占有率预测

在购买该药的总共1000家对象（购买力相当的医院、药店等）中，买A、B、C三药厂的各有400家、300家、300家，预测A、B、C三个厂家生产的某种抗病毒药在未来的市场占有情况。顾客订货情况如下表5：

表5 顾客订货情况表

下季度订货情况					合计
来自		A	B	C
	A	160	120	120		400
	B	180	90	30		300
	C	180	30	90		300
合计		520	240	240		1000

问题分析

目前的市场占有情况为：在购买该药的总共1000家对象（购买力相当的医院、药店等）中，买A、B、C三药厂的各有400家、300家、300家，那么A、B、C三药厂目前的市场占有份额分别为：40%、30%、30%．称（0.4，0.3，0.3）为目前市场的占有分布或称初始分布．

此外，我们需要查清使用对象的流动情况。流动情况的调查可通过发放信息调查表来了解顾客以往的资料或将来的购买意向，也可从下一时期的订货单得出。由题已知顾客订货情况如下表5

模型的建立

模型构建

假定在未来的时期内，顾客相同间隔时间的流动情况不因时期的不同而发生变化，以1、2、3分别表示顾客买A、B、C三厂家的药这三个状态，以季度为模型的步长（即转移一步所需的时间），那么根据表5，我们可以得模型的转移概率矩阵：

矩阵中的第一行（0.4，0.3，0.3）表示目前是A厂的顾客下季度有40%仍买A厂的药，转为买B厂和C厂的各有30%．同样，第二行、第三行分别表示目前是B厂和C厂的顾客下季度的流向．

由P我们可以计算任意的k步转移矩阵，如三步转移矩阵：

从这个矩阵的各行可知三个季度以后各厂家顾客的流动情况．如从第二行（0.504，0.252，0.244）知，B厂的顾客三个季度后有50.4%转向买A厂的药，25.2%仍买B厂的，24.4%转向买C厂的药．

设表示预测对象k季度以后的市场占有率，初始分布则为，市场占有率的预测模型为

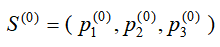
已知，由此，我们可预测任意时期A、B、C三厂家的市场占有率．例如，三个季度以后的预测值为：

大致上，A 厂占有一半的市场，B厂、C厂各占四分之一．

可推广到N个状态的情形：

如果我们按公式继续逐步求A、B、C三家的市场占有率，会发现，当k大到一定的程度，S (k) 将不会有多少改变，即有稳定的市场占有率，设其稳定值为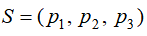，满足

事实上，如果市场的顾客流动趋向长期稳定下去，则经过一段时期以后的市场占有率将会出现稳定的平衡状态，即顾客的流动，不会影响市场的占有率，而且这种占有率与初始分布无关．如何求出这种稳定的市场占有率呢？

模型求解

以A、B、C三家的情况为例，当市场出现平衡状态时，从公式（7）可得方程S = S P，即

由此得

经整理，并加上条件，得

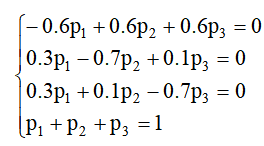
0.4 0.3 0.3，0.6 0.3 0.1,0.6 0.1 0.3

上方程组是三个变量四个方程的方程组，在前三个方程中只有二个是独立的，任意删去一个，从剩下的三个方程中，可求出唯一解：

这就是A、B、C三家的最终市场占有率．

一般N个状态的稳定市场占有率（稳态概率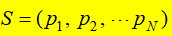）可通过解方程组

求得，而公式的前N个方程中只有N-1个是独立的，可任意删去一个。

MATLAB程序

format rat
p=[0.4 0.3 0.3，0.6 0.3 0.1,0.6 0.1 0.3];
a=[p'-eye(3);ones(1,3)];
b=[zeros(3,1);1];
p_limit=a\b

应用题型二：期望利润预测

企业追逐市场占有率的真正目的是使利润增加，因此，竞争各方无论是为了夺回市场份额，还是为了保住或者提高市场份额，在制订对策时都必须对期望利润进行预测．

预测主要分两步进行：

①市场统计调查．首先调查销路的变化情况，即查清由畅销到滞销或由滞销到畅销，连续畅销或连续滞销的可能性是多少．其次统计出由于销路的变化，获得的利润和亏损情况．
②建立数学模型，列出预测公式进行预测．

例如，通过市场调查，我们得到如下的销路转移表（表6）和利润变化表（表7）．由此，我们来建立数学模型．

表6 销路转移表

		畅销	滞销
		1	2
1	畅销	0.5	0.5
2	滞销	0.4	0.6

销路转移表说明连续畅销的可能性为50%，由畅销转入滞销的可能性也是50%，由滞销到畅销为40%，连续滞销的可能性为60%．利润表说明的是连续畅销获利900万元，由畅销到滞销或由滞销到畅销均获利300万元，连续滞销则亏损700万元．从而得到销售状态的转移矩阵P和利润矩阵R分别为：

表7 利润变化表（单位：百万元）

		畅销	滞销
		1	2
1	畅销	9	3
2	滞销	3	-7

模型构建

P和R便构成一个有利润的马氏链．由前面所述的基本原理及公式（6）得下面的预测公式：

即时期利润：

k步以后的期望利润：

模型求解

将调查数据代入上公式则可预测各时期的期望利润值．如：

由此可知，当本季度处于畅销时，在下一季度可以期望获得利润600万元；当本季度处于滞销时，下一季度将期望亏损300万元．

同样算得：

由此可预测本季度处于畅销时，两个季度后可期望获利750万元，三个季度后可期望获利855万元；当本季度处于滞销时，两个季度后将亏损240万元，三个季度后亏损144万元。

钢琴销售的存贮策略

背景与问题

钢琴销售

售量很小
商店的库存量不大以免积压资金
一家商店根据经验估计：平均每周的钢琴需求为1架

存贮策略

每周末检查库存量
仅当库存量为零时，才订购3架供下周销售
否则，不订购

问题

估计在这种策略下失去销售机会的可能性有多大，以及每周的平均销售量是多少。

分析与假设

需求：顾客的到达相互独立

需求量近似服从泊松分布，其参数由需求均值为每周1架确定→计算不同需求量的概率

失去销售机会：需求超过库存→动态过程→概率

存贮策略：周末库存量为零时订购3架, 周初到货；否则，不订购

周末的库存量：0, 1, 2, 3
周初的库存量：1, 2, 3共三种状态

用马氏链描述每周不同的需求导致周初库存状态的变化

以每周初的库存量作为状态变量
状态转移具有无后效性

在稳态情况下——时间充分长以后

计算该存贮策略失去销售机会的概率、每周的平均销售量

模型建立

模型求解

估计在这种策略下失去销售机会的可能性

第n周失去销售机会的概率

从长期看，失去销售机会的可能性大约 10%

估计这种策略下每周的平均销售量

第n周平均售量

从长期看，每周的平均销售量为 0.857(架)

敏感性分析

平均需求：每周1 (架) 附近波动时，结果有多大变化

设 $D_{n}$ 服从均值为 $\lambda$ 的柏松分布

状态转移阵

Matlab程序

第n周(n充分大)失去销售机会的概率：

for i=1:10
   lamda=0.5+0.1*i;
   d(i,1)=poisspdf(0,lamda); d(i,2)=poisspdf(1,lamda); d(i,3)=poisspdf(2,lamda);
   d(i,4)=poisspdf(3,lamda); d(i,5)=1-poisscdf(3,lamda);
   p1=[d(i,1) 0 1-d(i,1);d(i,2) d(i,1) 1-d(i,1)-d(i,2);d(i,3) d(i,2) 1-d(i,2)-d(i,3)]';
   [V,D]=eig(p1);  V1(i,:)=abs(V(:,1)/([1 1 1]*V(:,1)))';
   P(i)=[d(i,3)+d(i,4)+d(i,5),d(i,4)+d(i,5),d(i,5)]*V1(i,:)';
end
P

$\lambda$	0.8	0.9	1.0	1.1	1.2
P	0.073	0.089	0.105	0.122	0.139

当平均需求( $\lambda$ =1.0)增长（或减少）10%时，失去销售机会的概率将增长（或减少）约15%

存贮策略(周末库存为0则订购3架, 否则不订购)已定,计算两个指标(失去销售的概率和每周平均销售量).

关键是在无后效性的前提下恰当地定义系统的状态变量(本例是每周初的库存量).

动态随机存贮策略是马氏链的典型应用.

今天的文章马尔可夫链模型步骤_简单线性模型的高斯马可夫定理分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/81650.html

马尔可夫链模型步骤_简单线性模型的高斯马可夫定理

马尔可夫链的基本原理

马氏链严格数学定义

马氏链模型说明

转移概率矩阵

转移概率矩阵性质

气象案例的马尔可夫链表示

k步转移概率矩阵

气象案例的k步转移矩阵

状态转移概率

实例：求销售状态的转移概率矩阵

Matlab程序

正则链

<img decoding="async" src="https://img.bianchenghao.cn/app/bianchenghao_cn/f9ef9778fdd9.png" alt="马尔可夫链模型步骤_简单线性模型的高斯马可夫定理" title="马尔可夫链模型步骤_简单线性模型的高斯马可夫定理插图43" />

吸收链

马氏链的基本方程

带利润的马氏链

应用题型一：市场占有率预测

问题分析

模型的建立

模型构建

模型求解

MATLAB程序

应用题型二：期望利润预测

模型构建

模型求解

钢琴销售的存贮策略

背景与问题

分析与假设

模型建立

模型求解

敏感性分析

Matlab程序

相关推荐

发表回复