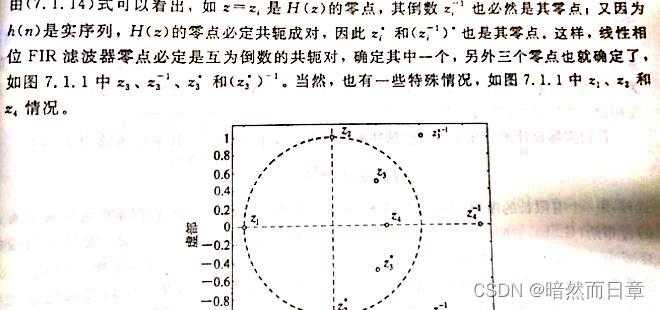
数字信号处理翻转课堂笔记16
The Flipped Classroom16 of DSP
对应教材:《数字信号处理(第五版)》西安电子科技大学出版社,丁玉美、高西全著
一、要点
(1)两类线性相位的概念;
(2)线性相位FIR滤波器的时域约束条件(重点);
(3)第一类线性相位FIR滤波器幅度特性的特点(重点);
(4)第二类线性相位FIR滤波器幅度特性的特点;
(5)线性相位FIR滤波器零点分布的特点。
二、问题与解答
1、什么是线性相位?线性相位的实质是什么?结合实际应用问题,说明线性相位在信号滤波、信号传输方面有什么意义?
2、第一类线性相位和第二类线性相位有什么区别?第二类线性相位能否实现无失真传输?试举例说明(用一个包含若干个频率分量的信号来演示)。对于起始相位固定为-0.5π的第二类线性相位,可以采用何种措施来实现无失真传输(移相器)?
3、自定一个满足第一类线性相位时域约束条件的FIR滤波器h(n),基于MATLAB,分别画出滤波器长度为奇数和偶数时的滤波器幅度特性(注意区分这里的幅度特性,它不等同于幅频特性。请利用教材式7.1.11和7.1.12画幅度特性曲线)和相频特性曲线,绘图区间范围取4π。验证其是否具有第一类线性相位,总结这两种滤波器幅度特性的特点和周期性,分析其适用的数字滤波器类型。
4、自定一个满足第二类线性相位时域约束条件的FIR滤波器h(n),基于MATLAB,分别画出滤波器长度为奇数和偶数时的滤波器幅度特性(参考教材中相应公式 )和相频特性曲线,绘图区间范围取4π。验证其是否具有第二类线性相位,总结这两种滤波器幅度特性的特点和周期性,分析其适用的数字滤波器类型。
5、针对第(3)题和第(4)题的各种情形(可采用与这两题相同的h(n),但应避免零点分布情况过于单一),分别画出FIR滤波器的零极点图(注意绘图的时候,分母向量应该与分子向量同维,例如A=[1 0 0 0 0 0 0 0 ])。总结各种情形零极点分布的共同特性,分析每种情形零点分布的独有特点。
6、
1、线性相位的含义及实用意义
什么是线性相位?线性相位的实质是什么?结合实际应用问题,说明线性相位在信号滤波、信号传输方面有什么意义?
1)相位与系统的相频响应成正比。
线性相位FIR滤波器指θ(ω)是ω的线性函数。即:
θ(ω)=-τω (τ为常数)
2)线性相位的实质是所有不同的频率分量具有相同的时间延迟。
3)意义:线性相位是信号的无失真传输的必要条件。
2、两类线性相位的特点
第一类线性相位和第二类线性相位有什么区别?第二类线性相位能否实现无失真传输?试举例说明(用一个包含若干个频率分量的信号来演示)。对于起始相位固定为-0.5π的第二类线性相位,可以采用何种措施来实现无失真传输(移相器)?
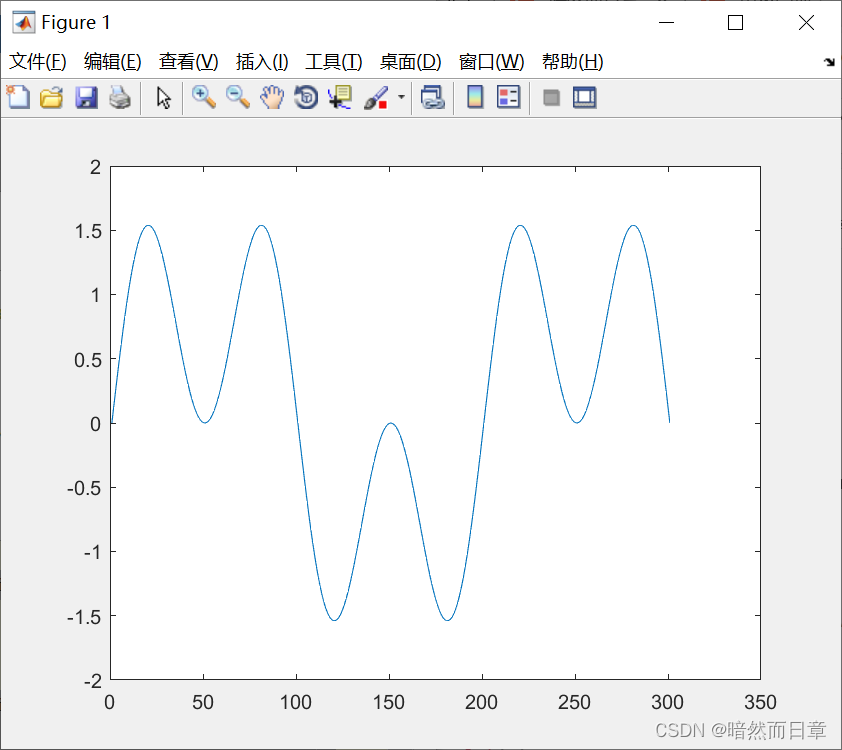
n=0:300;
s=sin(0.01*pi*n)+sin(0.03*pi*n);
figure(1)
plot(s)
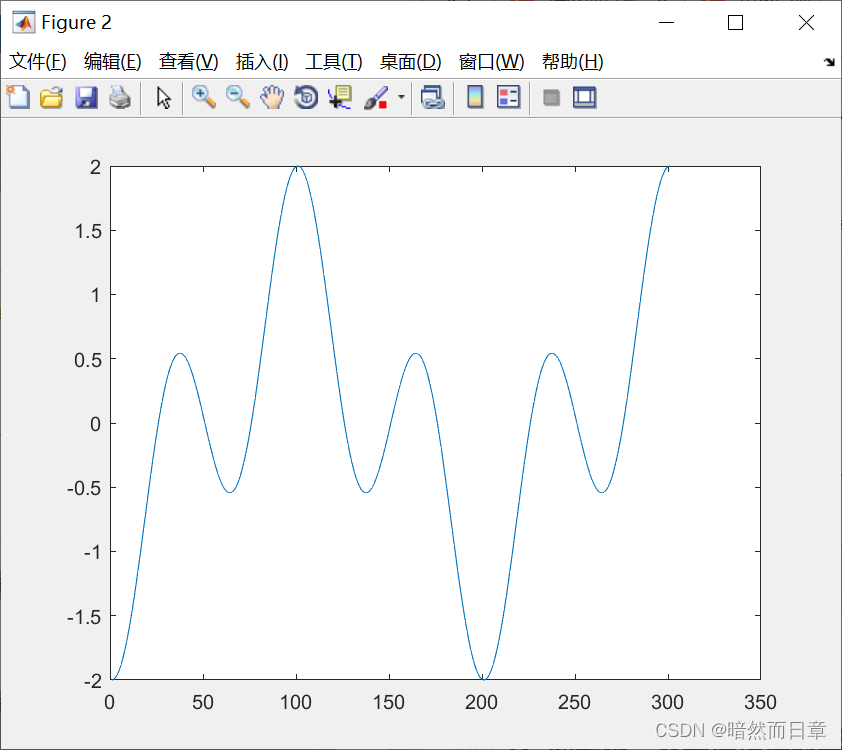
%% 相位滞后0.5π
x=sin(0.01*pi*n-0.5*pi)+sin(0.03*pi*n-0.5*pi); %传输失真信号:第二类线性相位
figure(2)
plot(x)
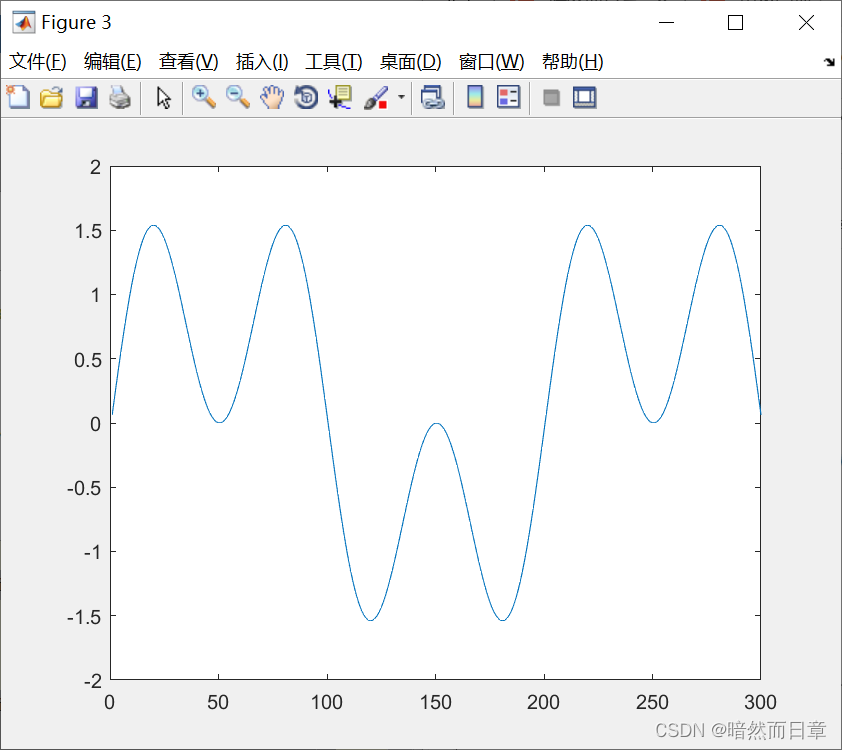
x1=1/0.01/pi*sin(0.01*pi*n+0.5*pi)+1/0.03/pi*sin(0.03*pi*n+0.5*pi); %幅度补偿:频率的倒数,除以0.01π,除以0.03π
y=-diff(x1); %移相90度:求差分并取反
figure(3)
plot(y)
对于起始相位固定为-0.5π的第二类线性相位,可以采用求差分并取反来实现无失真传输。
3、满足第一类线性相位时域约束条件的FIR滤波器
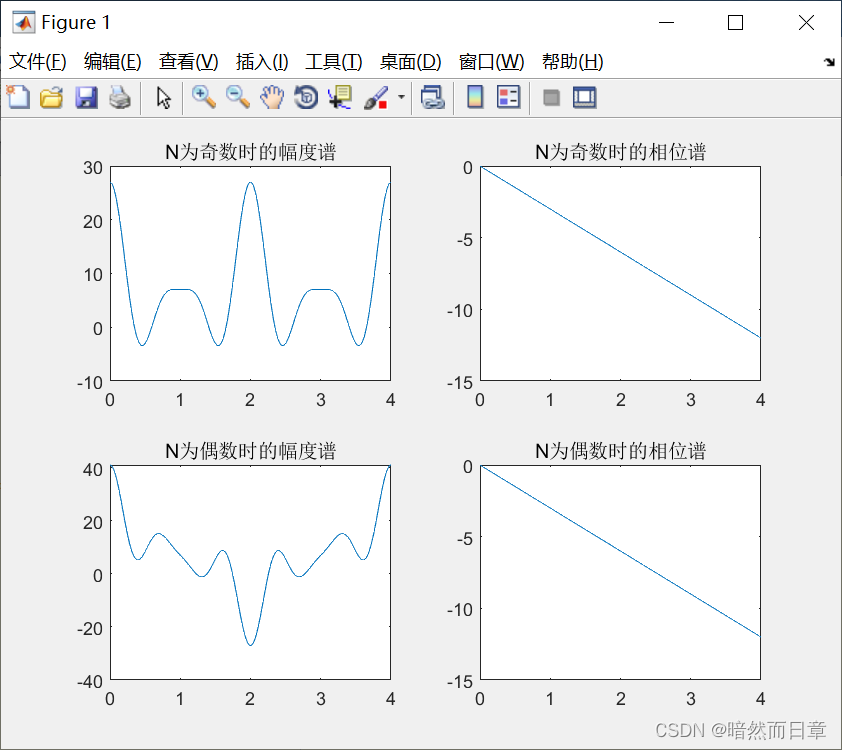
自定一个满足第一类线性相位时域约束条件的FIR滤波器h(n),基于MATLAB,分别画出滤波器长度为奇数和偶数时的滤波器幅度特性(注意区分这里的幅度特性,它不等同于幅频特性。请利用教材式7.1.11和7.1.12画幅度特性曲线)和相频特性曲线,绘图区间范围取4π。验证其是否具有第一类线性相位,总结这两种滤波器幅度特性的特点和周期性,分析其适用的数字滤波器类型。
代码如下:
t=3;
h=[2 5 3 7 3 5 2];
a=1;
fudu=zeros(1,401);
for w=0:400
for n=0:2
fudu(a)=fudu(a)+2*h(n+1)*cos(w/100*pi*(n-t));
end
a=a+1;
end
fudu=fudu+h(4);
subplot(2,2,1)
plot(0:1/100:4,fudu)
title('N为奇数时的幅度谱');
subplot(2,2,2)
w=0:1/100:4;
xiangwei=-w*3;
plot(w,xiangwei)
title('N为奇数时的相位谱');
N=8;
t=3.5;
h=[2 5 3 7 7 3 5 2];
a=1;
fudu=zeros(1,401);
for w=0:400
for n=0:3
fudu(a)=fudu(a)+2*h(n+1)*cos(w/100*pi*(n-t));
end
a=a+1;
end
fudu=fudu+h(4);
subplot(2,2,3)
plot(0:1/100:4,fudu)
title('N为偶数时的幅度谱');
subplot(2,2,4)
w=0:1/100:4;
xiangwei=-w*3;
plot(w,xiangwei)
title('N为偶数时的相位谱');
运行结果:
具有第一类线性相位
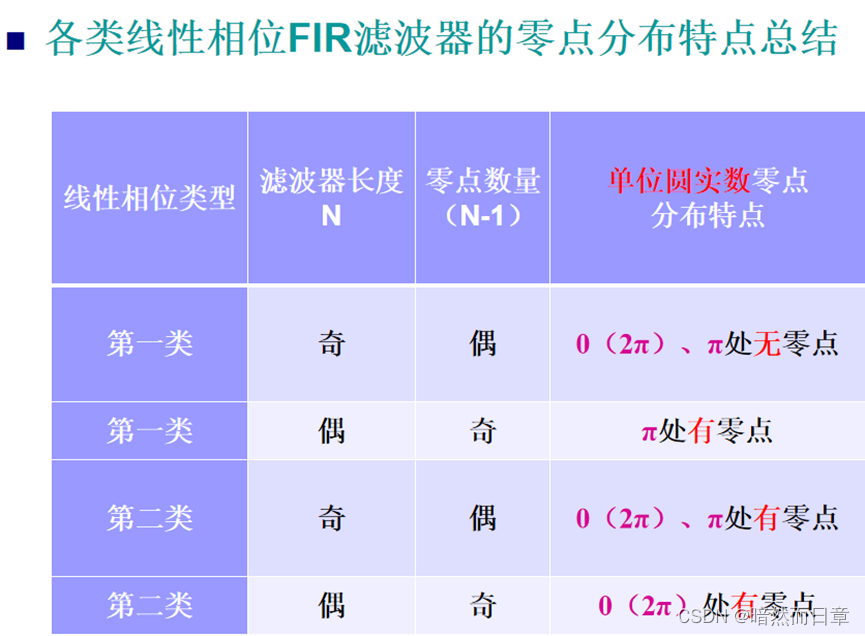
第一类滤波器幅度特点:以2π为周期;关于w=0, π, 2π偶对称;适用于各类滤波器。
第二类滤波器幅度特性:以4π为周期;关于w=π, 3π奇对称;关于w=0,2π偶对称;不能作高通,带阻滤波器。
4、满足第二类线性相位时域约束条件的FIR滤波器
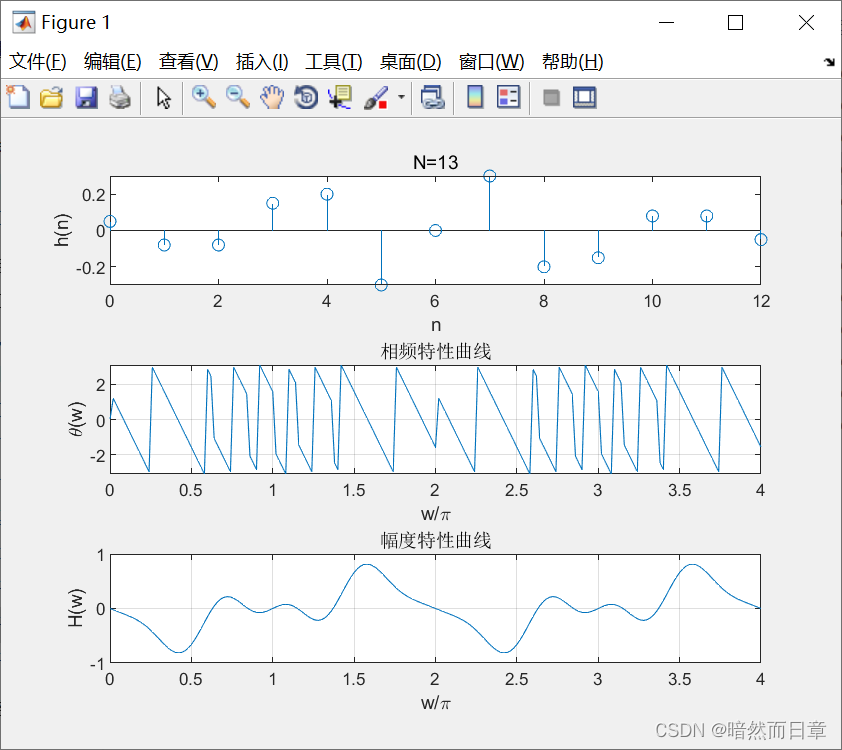
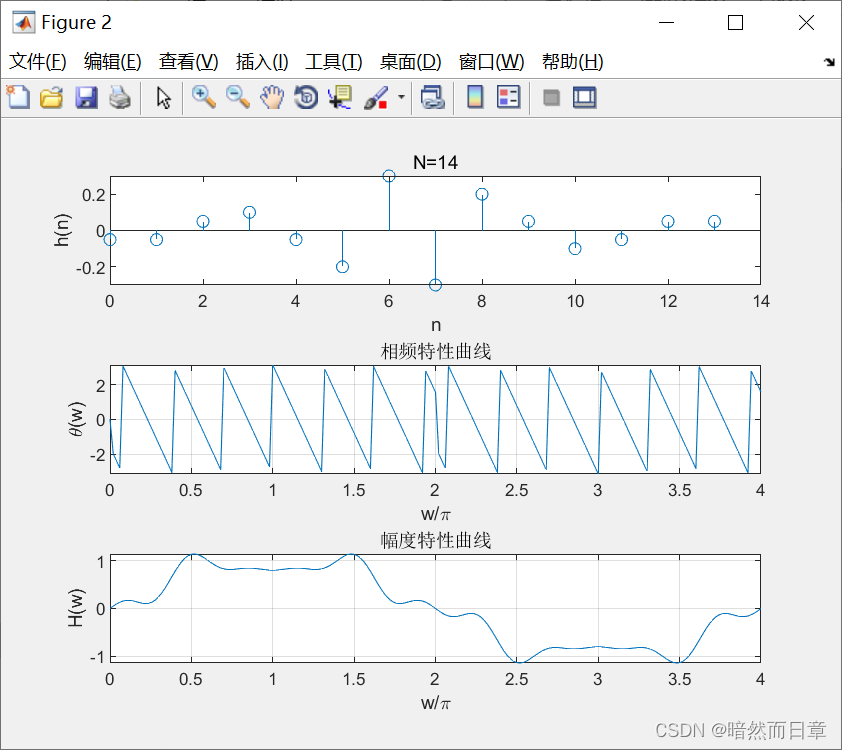
自定一个满足第二类线性相位时域约束条件的FIR滤波器h(n),基于MATLAB,分别画出滤波器长度为奇数和偶数时的滤波器幅度特性(参考教材中相应公式 )和相频特性曲线,绘图区间范围取4π。验证其是否具有第二类线性相位,总结这两种滤波器幅度特性的特点和周期性,分析其适用的数字滤波器类型。
N=13;
h=[0.05,-0.08,-0.08,0.15,0.2,-0.3,0,0.3,-0.2,-0.15,0.08,0.08,-0.05];
n=0:N-1;
figure(1)
subplot(3,1,1)
stem(n,h)
xlabel('n')
ylabel('h(n)')
title('N=13')
t=(N-1)/2;
M=(N-1)/2;
k=0:0.01:2;
w=2*pi*k;
tao=-pi/2-w*t;%相位函数
H=0;
for n=1:M;
H=H+2*h(n)*sin(w*(n-t));
end
H1=H.*exp(j*tao);
H_angle=angle(H1);
subplot(3,1,2)
plot(w/pi,H_angle)
grid on
xlabel('w/\pi')
ylabel('\theta(w)')
title('相频特性曲线')
subplot(3,1,3)
plot(w/pi,H)
grid on
xlabel('w/\pi')
ylabel('H(w)')
title('幅度特性曲线')
figure(2)
N=14;
h=[-0.05,-0.05,0.05,0.1,-0.05,-0.2,0.3,-0.3,0.2,0.05,-0.1,-0.05,0.05,0.05];
n=0:N-1;
subplot(3,1,1)
stem(n,h)
xlabel('n')
ylabel('h(n)')
title('N=14')
t=(N-1)/2;
M=(N-1)/2;
k=0:0.01:2;
w=2*pi*k;
tao=-pi/2-w*t;%相位函数
H=0;%2*(0.05)*sin(w*(-t));
for n=1:M+1;
H=H+2*h(n)*sin(w*(n-t));
end
H1=H.*exp(j*tao);
H_angle=angle(H1);
subplot(3,1,2)
plot(w/pi,H_angle)
grid on
xlabel('w/\pi')
ylabel('\theta(w)')
title('相频特性曲线')
subplot(3,1,3)
plot(w/pi,H)
grid on
xlabel('w/\pi')
ylabel('H(w)')
title('幅度特性曲线')
运行结果:
当滤波器长度为奇数时,其幅频特性曲线关于三点奇对称,并且以2为周期,因此这种情况的滤波器只适用带通滤波器。
当滤波器长度为偶数时,以4为周期,这种滤波器不能实现低通和带阻滤波器,可以实现高通、带通滤波器。
5、第一类与第二类FIR滤波器的零极点图
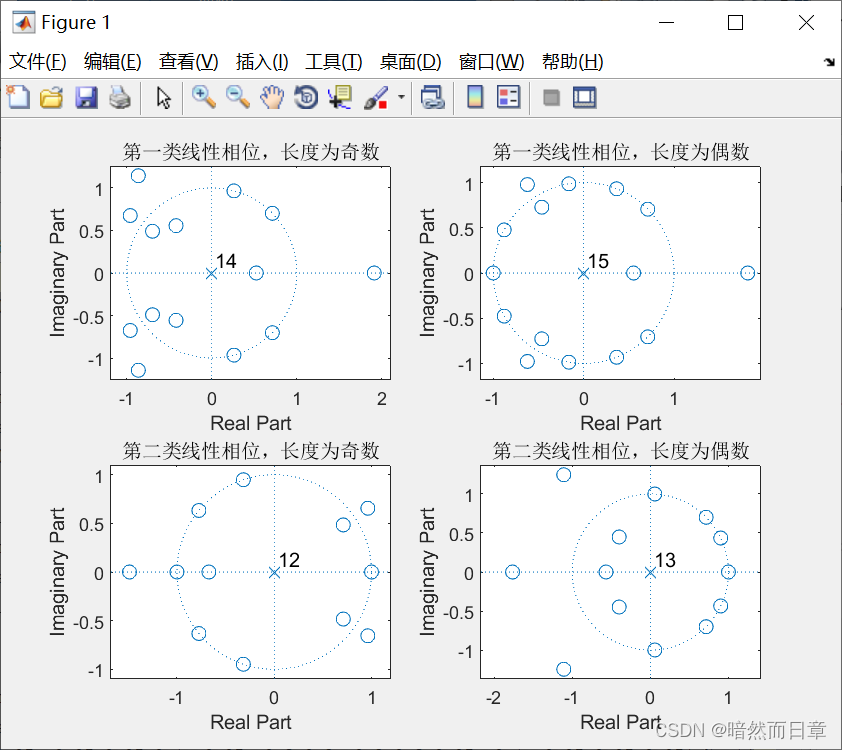
针对第(3)题和第(4)题的各种情形(可采用与这两题相同的h(n),但应避免零点分布情况过于单一),分别画出FIR滤波器的零极点图(注意绘图的时候,分母向量应该与分子向量同维,例如A=[1 0 0 0 0 0 0 0 ])。总结各种情形零极点分布的共同特性,分析每种情形零点分布的独有特点。
h=[-0.02,-0.03,0,0.1,0.13,0.13,0.14,0.2,0.14,0.13,0.13,0.1,0,-0.03,-0.02];%N=15
A=[1,0,0,0,0,0,0,0,0,0,0,0,0,0,0];
subplot(2,2,1)
zplane(h,A)
title('第一类线性相位,长度为奇数')
h=[-0.04,-0.03,0,0.1,0.15,0.2,0.25,0.28,0.28,0.25,0.2,0.15,0.1,0,-0.03,-0.04];
A=[1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0];
subplot(2,2,2)
zplane(h,A)
title('第一类线性相位,长度为偶数')
subplot(2,2,3)
h=[0.06,0.06,-0.12,-0.1,0.12,0.2,0,-0.2,-0.12,0.1,0.12,-0.06,-0.06];%N=13
A=[1,0,0,0,0,0,0,0,0,0,0,0,0];
zplane(h,A)
title('第二类线性相位,长度为奇数')
h=[-0.05,-0.05,0.05,0.1,-0.05,-0.2,0.3,-0.3,0.2,0.05,-0.1,-0.05,0.05,0.05];%N=14
A=[1,0,0,0,0,0,0,0,0,0,0,0,0,0];
subplot(2,2,4)
zplane(h,A)
title('第二类线性相位,长度为偶数')
6、滤波器综合性题目
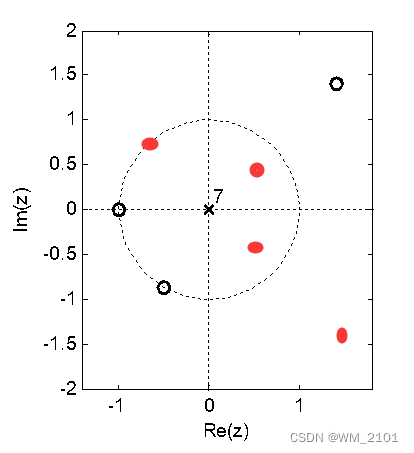
a)
有7个零点,所以滤波器长度为8
b)
z=-1处有零点,具有第一类线性相位,幅度特性:
c)
不是,因为相位π处幅度为0,不可能为高通。
d)
情况1:若增加的零点加在1,偶对称*奇对称=奇对称,具有第二类线性特性,长度为9,不为高通滤波器、也不为低通滤波器
情况2:若增加的零点在-1,即为二重零点,偶对称*偶对称=偶对称,具有第一类线性特性,不为高通滤波器。
此处注意要分类讨论,不要漏情况。
三、反思总结
今天的文章数字信号处理matlab版答案_数字信号处理实验报告MATLAB分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/81905.html