1. 编程号首页

求原根的方法_解不等式的例题及答案

编程小号 • • 未分类

求原根的方法_解不等式的例题及答案1.原根定义假设一个数g对于P来说是原根，那么g^imodP的结果两两不同,且有1简单来说，g^imodp≠g^jmodp（p为素数）其中i≠j且i,j介於1至(p-1)之间则g为p的原根

1.原根定义

假设一个数g对于P来说是原根，那么g^i mod P的结果两两不同,且有 1<g<P, 1<i<P,那么g可以称为是P的一个原根
简单来说，g^i mod p ≠ g^j mod p （p为素数）
其中i≠j且i, j介於1至(p-1)之间
则g为p的原根。
 
简单的来说，如果g是P的原根，那么g的（1…P-1）次幂mod P的结果一定互不相同。
 
那么简化一下：
首先看一下欧拉定理：

欧拉定理（也称费马-欧拉定理或欧拉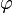{\varphi}函数定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互素（即\gcd(a,n)=1），则


a^{\varphi(n)} \equiv 1 \pmod n

因此，在
gcd(a,m)=1时，定义
a对模m的指数
Ord_m(a)为使
a^d \equiv 1 \pmod{m}成立的最小的正整数
d。由前知
Ord_m(a) 一定小于等于 
\phi (m)，若
Ord_m (a) = \phi (m)，则称
a是模m的原根。
 
归根到底，如果g是P的原根，就是g^(P-1) = 1 (mod P)当且仅当指数为P-1的时候成立.(这里P是素数).
 
 
 
例如：
设
m= 7，则φ（7）等于6。φ（7）表示7的欧拉函数。
设
a= 2，由于2^3=8≡1(mod 7)，而3<6，所以 2 不是模 7 的一个原根。设
a= 3，由于3^1≡3(mod 7)，3^2≡2(mod 7)，3^3≡6(mod 7)，3^4≡4(mod 7)，3^5≡5(mod 7)，3^6≡1(mod 7)，所以 3 是模 7 的一个原根。
 

2.如何求解：

一、枚举

从2开始枚举，然后暴力判断g^(P-1) = 1 (mod P)是否当且当指数为P-1的时候成立

而由于原根一般都不大，所以可以暴力得到.

二、讲究方法

例如求任何一个质数x的任何一个原根，一般就是枚举2到x-1，并检验。有一个方便的方法就是，求出x-1所有不同的质因子p1,p2…pm，对于任何2<=a<=x-1,判定a是否为x的原根，只需要检验a^((x-1)/p1),a^((x-1)/p2),…a^((x-1)/pm)这m个数中，是否存在一个数mod x为1，若存在，a不是x的原根，否则就是x的原根。

原来的复杂度是O(P-1)，现在变成O(m)*log（P-1）m为x-1质因子的个数。很明显质因子的个数远远小于x-1。

证明可用欧拉定理和裴蜀定理：

裴蜀定理

说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）：

ax + by = m 
有解当且仅当m是d的倍数。裴蜀等式有解时必然有无穷多个整数解，每组解x、y都称为裴蜀数，可用辗转相除法求得。

例如，12和42的最大公因子是6，则方程12x + 42y = 6有解。事实上有(-3)×12 + 1×42 = 6及4×12 + (-1)×42 = 6。

特别来说，方程 ax + by = 1 有解当且仅当整数a和b互素。

裴蜀等式也可以用来给最大公约数定义：d其实就是最小的可以写成ax + by形式的正整数。这个定义的本质是整环中“理想”的概念。因此对于多项式整环也有相应的裴蜀定理。


证明

[html]  view plain   copy

  1. 若存在，那么显然的事情  
  2.   
  3. 否则，假设存在一个t<phi(x)=x-1使得a^t = 1 (mod x)  
  4.   
  5. 那么由裴蜀定理，一定存在一组k,r使得kt=(x-1)r+gcd(t,x-1)  
  6.   
  7. 而由欧拉定理有，a^(x-1) = 1 (mod x)  
  8.   
  9. 于是1 = a^(kt) = a^(xr-r+gcd(t,x-1)) = a^gcd(t,x-1) (mod x)  
  10.   
  11. 而t<x-1故gcd(t,x-1)<x-1  
  12.   
  13. 又gcd(t,x-1)|x-1 于是gcd(t,x-1)必整除(x-1)/p1,(x-1)/p2…(x-1)/pm其中至少一个，设其一为(x-1)/pi  
  14.   
  15. 那么a^((x-1)/pi) = (a^gcd(t,x-1))^s = 1^s = 1 (mod x)  
  16.   
  17. 这与假设矛盾  

代码：

来至http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1135的一道题目：

题目


设m是正整数，a是整数，若a模m的阶等于φ(m)，则称a为模m的一个原根。（其中φ(m)表示m的欧拉函数）


给出1个质数P，找出P最小的原根。


Input
<span id="Showjim86_bnbbbsbl_s39"></span>输入1个质数P(3 <= P <= 10^9)<span id="Showjim86_bnbbbsbl_e39"></span>
Output
<span id="Showjim86_bnbbbsbl_s40"></span>输出P最小的原根。

解答

[cpp]  view plain   copy

  1. #include <iostream>  
  2. #include <cstdlib>  
  3. #include <cstring>  
  4. #include <cstdio>  
  5. using namespace std;  
  6. int P;  
  7. const int NUM = 32170;  
  8. int prime[NUM/4];  
  9. bool f[NUM];  
  10. int pNum = 0;  
  11. void getPrime()//线性筛选素数  
  12. {  
  13.     for (int i = 2; i < NUM; ++ i)  
  14.     {  
  15.         if (!f[i])  
  16.         {  
  17.             f[i] = 1;  
  18.             prime[pNum++] = i;  
  19.         }  
  20.         for (int j = 0; j < pNum && i*prime[j] < NUM; ++ j)  
  21.         {  
  22.             f[i*prime[j]] = 1;  
  23.             if (i%prime[j] == 0)  
  24.             {  
  25.                 break;  
  26.             }  
  27.         }  
  28.     }  
  29. }  
  30. __int64 getProduct(int a,int b,int P)//快速求次幂mod  
  31. {  
  32.     __int64 ans = 1;  
  33.     __int64 tmp = a;  
  34.     while (b)  
  35.     {  
  36.         if (b&1)  
  37.         {  
  38.             ans = ans*tmp%P;  
  39.         }  
  40.         tmp = tmp*tmp%P;  
  41.         b>>=1;  
  42.     }  
  43.     return ans;  
  44. }  
  45.   
  46. bool judge(int num)//求num的所有的质因子  
  47. {  
  48.     int elem[1000];  
  49.     int elemNum = 0;  
  50.     int k = P – 1;  
  51.     for (int i = 0; i < pNum; ++ i)  
  52.     {  
  53.         bool flag = false;  
  54.         while (!(k%prime[i]))  
  55.         {  
  56.             flag = true;  
  57.             k /= prime[i];  
  58.         }  
  59.         if (flag)  
  60.         {  
  61.             elem[elemNum ++] = prime[i];  
  62.         }  
  63.         if (k==1)  
  64.         {  
  65.             break;  
  66.         }  
  67.         if (k/prime[i]<prime[i])  
  68.         {  
  69.             elem[elemNum ++] = prime[i];  
  70.             break;  
  71.         }  
  72.     }  
  73.     bool flag = true;  
  74.     for (int i = 0; i < elemNum; ++ i)  
  75.     {  
  76.         if (getProduct(num,(P-1)/elem[i],P) == 1)  
  77.         {  
  78.             flag = false;  
  79.             break;  
  80.         }  
  81.     }  
  82.     return flag;  
  83. }  
  84. int main()  
  85. {  
  86.       
  87.     getPrime();  
  88.     while (cin >> P)  
  89.     {  
  90.         for (int i = 2;;++i)  
  91.         {  
  92.             if (judge(i))  
  93.             {  
  94.                 cout << i<< endl;  
  95.                 break;  
  96.             }  
  97.         }  
  98.     }  
  99.     return 0;  
  100. }  

今天的文章求原根的方法_解不等式的例题及答案分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/81937.html

赞 (0)
编程小号编程小号
0

相关推荐

发表回复

您的电子邮箱地址不会被公开。 必填项已用 * 标注