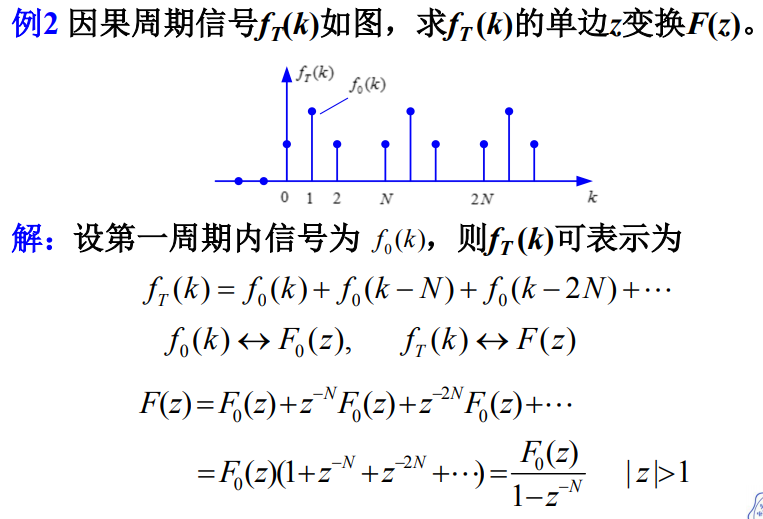
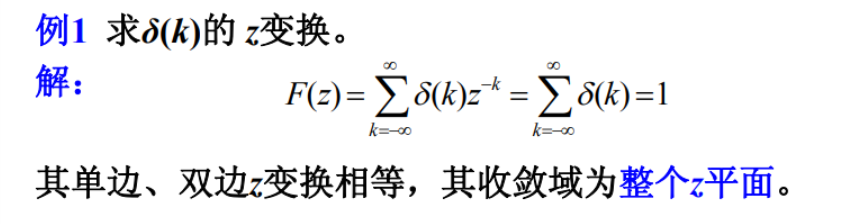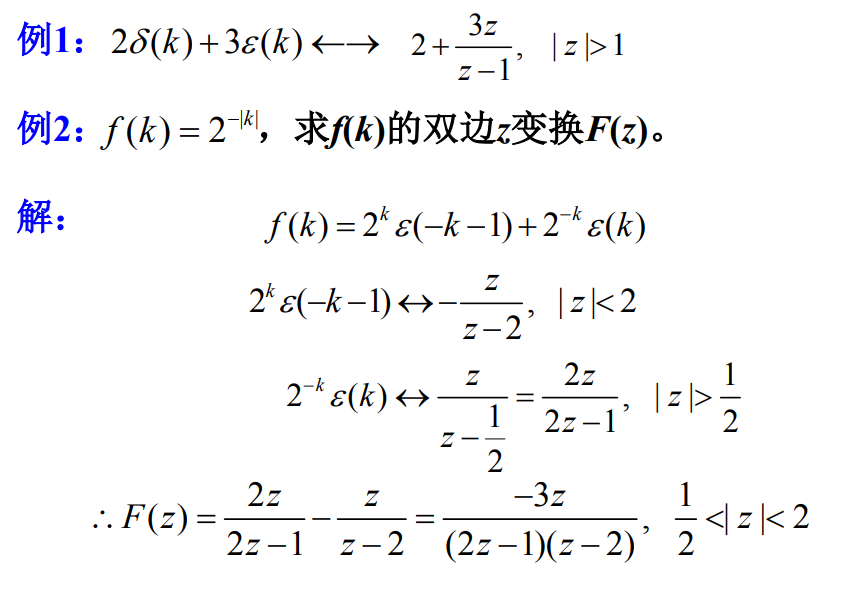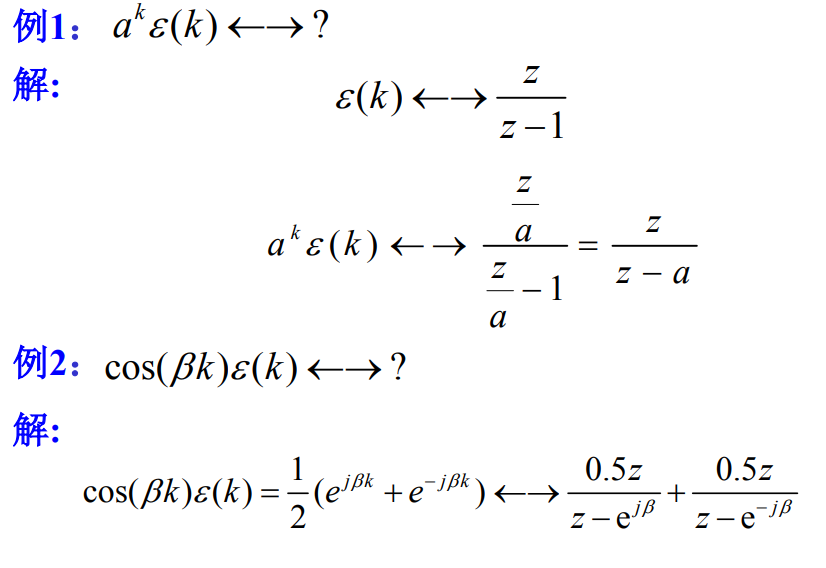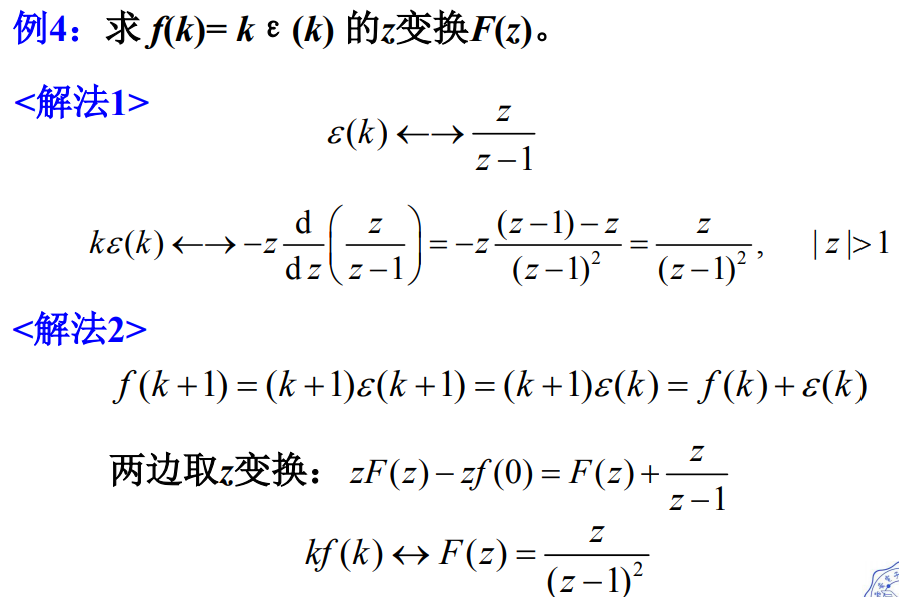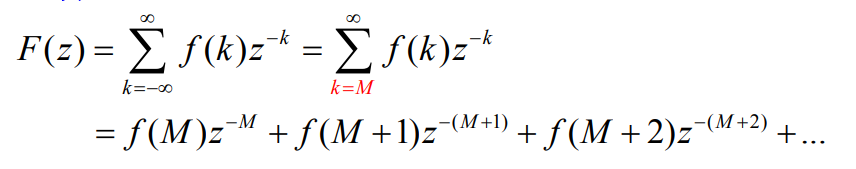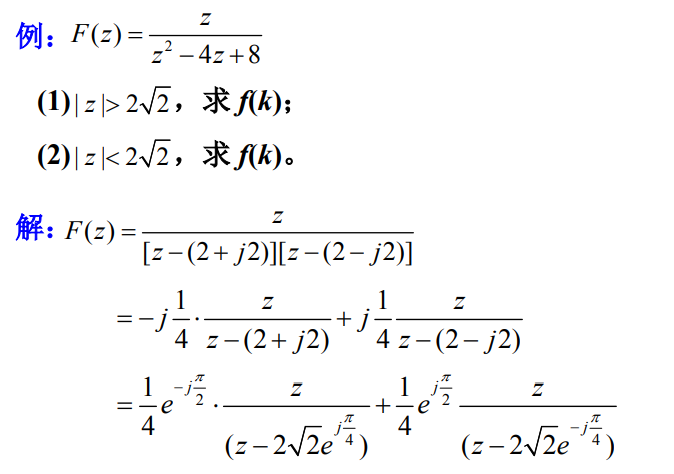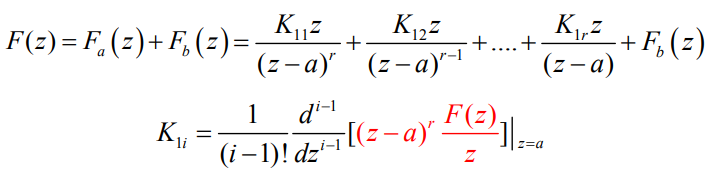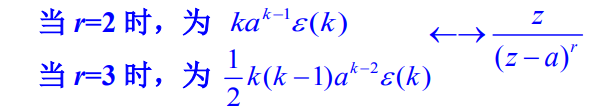文章目录
z变换及其性质
1 z变换定义及收敛域
拉氏变换把连续系统微分方程转换为代数方程,同样地,也可以通过一种称为 z z z变换的数学工具,把差分方程转换为代数方程。
1 z变换导出
对连续信号进行均匀冲激取样后,就得到离散信号。
取样信号:
f S ( t ) = f ( t ) δ T ( t ) = ∑ k = − ∞ ∞ f ( k T ) δ ( t − k T ) f_{S}(t)=f(t) \delta_{T}(t)=\sum_{k=-\infty}^{\infty} f(k T) \delta(t-k T) fS(t)=f(t)δT(t)=k=−∞∑∞f(kT)δ(t−kT)
两边取双边拉普拉斯变换,得:
F S b ( s ) = ∑ k = − ∞ ∞ f ( k T ) e − k T s F_{S b}(s)=\sum_{k=-\infty}^{\infty} f(k T) \mathrm{e}^{-k T s} FSb(s)=k=−∞∑∞f(kT)e−kTs
令 z = e s T z=e^{sT} z=esT,上式将成为复变量 z z z的函数,用 F ( z ) F(z) F(z)表示; f ( k T ) → f ( k ) f(k T) \rightarrow f(k) f(kT)→f(k),得到:
F ( z ) = ∑ k = − ∞ ∞ f ( k ) z − k F(z)=\sum_{k=-\infty}^{\infty} f(k) z^{-k} F(z)=k=−∞∑∞f(k)z−k
称为序列 f ( k ) f(k) f(k)的双边z变换。
F ( z ) = ∑ k = 0 ∞ f ( k ) z − k F(z)=\sum_{k=0}^{\infty} f(k) z^{-k} F(z)=k=0∑∞f(k)z−k
称为序列 f ( k ) f(k) f(k)的单边z变换
若 f ( k ) f(k) f(k)为因果序列,则单边、双边z变换相等,否则不同。今后在不致混淆的情况下,统一称它们为z变换。
表示为:
F ( z ) = Z [ f ( k ) ] , f ( k ) = Z − 1 [ F ( z ) ] F(z)=\mathscr{Z}[f(k)], f(k)=\mathscr{Z}^{-1}[F(z)] F(z)=Z[f(k)],f(k)=Z−1[F(z)] f ( k ) ← → F ( z ) f(k) \leftarrow \rightarrow F(z) f(k)←→F(z)
2 收敛域
当幂级数收敛时,z变换才存在,即满足绝对可和条件:
∑ k = − ∞ ∞ ∣ f ( k ) z − k ∣ < ∞ \sum_{k=-\infty}^{\infty}\left|f(k) z^{-k}\right|<\infty k=−∞∑∞∣∣f(k)z−k∣∣<∞
它是序列 f ( k ) f(k) f(k)的 z 变换存在的充分条件。
定义:收敛域
对于序列 f ( k ) f(k) f(k),满足 ∑ k = − ∞ ∞ ∣ f ( k ) z − k ∣ < ∞ \sum_{k=-\infty}^{\infty}\left|f(k) z^{-k}\right|<\infty ∑k=−∞∞∣∣f(k)z−k∣∣<∞的所有z值组成的集合称为其z变换 F ( z ) F(z) F(z)的收敛域。
有限长序列:
δ ( k ) z − k = δ ( k ) ⋅ 1 \delta(k)z^{-k}=\delta(k)\cdot 1 δ(k)z−k=δ(k)⋅1
画出 ε ( k + 1 ) − ε ( k − 2 ) \varepsilon(k+1)-\varepsilon(k-2) ε(k+1)−ε(k−2)的图。
等比数列求和公式:
a 1 ( 1 − q n ) 1 − q \frac{a_1(1-q^n)}{1-q} 1−qa1(1−qn)
例3中数列范围为( 0 ∼ N 0\sim N 0∼N)
双边序列的 z z z变换收敛域为环形或不存在:
离散序列的收敛域情况分类:
| 序列特性 | 收敛域特性 |
|---|---|
| 有限长序列 | 常为整个平面 |
| 因果序列 | 某个圆外区域 |
| 反因果序列 | 某个圆内区域 |
| 双边序列 | (若存在)环状区域 |
注意:双边 z 变换必须标明收敛域! 不同函数z变换相同,但收敛域可能不同,如:
f 1 ( k ) = 2 k ε ( k ) ← → 1 ( z ) = z z − 2 , ∣ z ∣ > 2 f_{1}(k)=2^{k} \varepsilon(k) \leftarrow \rightarrow_{1}(z)=\frac{z}{z-2},|z|>2 f1(k)=2kε(k)←→1(z)=z−2z,∣z∣>2
f 2 ( k ) = − 2 k ε ( − k − 1 ) ← → F 2 ( z ) = z z − 2 , ∣ z ∣ < 2 f_{2}(k)=-2^{k} \varepsilon(-k-1) \leftarrow \rightarrow F_{2}(z)=\frac{z}{z-2},|z|<2 f2(k)=−2kε(−k−1)←→F2(z)=z−2z,∣z∣<2
对单边 z z z变换,其收敛域都是某个圆外的区域,所以收敛域可省略。
结论:
双边 F b ( z ) + 收敛域 ⟶ f ( k ) \text { 双边 } F_{b}(z)+\text { 收敛域 } \longrightarrow f(k) 双边 Fb(z)+ 收敛域 ⟶f(k)
单边 F ( z ) ⟶ f ( k ) \text { 单边 } F(z)\longrightarrow f(k) 单边 F(z)⟶f(k)
2 常用序列的z变换
δ ( k ) ← → 1 , 整个z平面 \delta(k) \leftarrow \rightarrow 1, \quad \text { 整个z平面 } δ(k)←→1, 整个z平面
f 1 ( k ) = a k ε ( k ) ← → F 1 ( z ) = z z − a , ∣ z ∣ > ∣ a ∣ f_{1}(k)=a^{k} \varepsilon(k) \leftarrow \rightarrow F_{1}(z)=\frac{z}{z-a},|z|>|a| f1(k)=akε(k)←→F1(z)=z−az,∣z∣>∣a∣
f 2 ( k ) = − a k ε ( − k − 1 ) ← → F 2 ( z ) = z z − a , ∣ z ∣ < ∣ a ∣ f_{2}(k)=-a^{k} \varepsilon(-k-1) \leftarrow \rightarrow F_{2}(z)=\frac{z}{z-a},|z|<|a| f2(k)=−akε(−k−1)←→F2(z)=z−az,∣z∣<∣a∣
δ ( k − m ) ← → z − m , ∣ z ∣ > 0 \delta(k-m) \leftarrow \rightarrow z^{-m}, \quad|z|>0 δ(k−m)←→z−m,∣z∣>0
ε ( k ) ← → z z − 1 , ∣ z ∣ > 1 \varepsilon(k)\leftarrow \rightarrow\frac{z}{z-1},|z|\gt 1 ε(k)←→z−1z,∣z∣>1
ε ( − k − 1 ) ← → z z − 1 , ∣ z ∣ < 1 \varepsilon(-k-1)\leftarrow \rightarrow\frac{z}{z-1},|z|\lt1 ε(−k−1)←→z−1z,∣z∣<1
单边因果指数序列: a k ε ( k ) ← → z z − a , ∣ z ∣ > ∣ a ∣ a^k\varepsilon(k)\leftarrow \rightarrow\frac{z}{z-a},\quad |z|\gt |a| akε(k)←→z−az,∣z∣>∣a∣
左边指数序列: − a k ε ( − k − 1 ) ← → z z − a , ∣ z ∣ < ∣ a ∣ -a^k\varepsilon(-k-1)\leftarrow \rightarrow\frac{z}{z-a},\quad |z|\lt |a| −akε(−k−1)←→z−az,∣z∣<∣a∣
3 z变换性质
3.1 线性、移序、反折
说明:z变换性质,若无特殊说明,对单边和双边z变换均适用。
1、线性
f 1 ( k ) ↔ F 1 ( z ) , α 1 < ∣ z ∣ < β 1 f_{1}(k) \leftrightarrow F_{1}(z), \quad \alpha_{1}<|z|<\beta_{1} f1(k)↔F1(z),α1<∣z∣<β1
f 2 ( k ) ↔ F 2 ( z ) , α 2 < ∣ z ∣ < β 2 f_{2}(k) \leftrightarrow F_{2}(z), \quad \alpha_{2}<|z|<\beta_{2} f2(k)↔F2(z),α2<∣z∣<β2
a 1 f 1 ( k ) + a 2 f 2 ( k ) ↔ a 1 F 1 ( z ) + a 2 F 2 ( z ) a 1 , a 2 为任意常数 a_{1} f_{1}(k)+a_{2} f_{2}(k) \leftrightarrow a_{1} F_{1}(z)+a_{2} F_{2}(z) \quad \boldsymbol{a}_{1}, \boldsymbol{a}_{2} \text { 为任意常数 } a1f1(k)+a2f2(k)↔a1F1(z)+a2F2(z)a1,a2 为任意常数
max ( α 1 , α 2 ) < ∣ z ∣ < min ( β 1 , β 2 ) \max \left(\alpha_{1}, \alpha_{2}\right)<|z|<\min \left(\beta_{1}, \beta_{2}\right) max(α1,α2)<∣z∣<min(β1,β2)
注:其收敛域至少是 F 1 ( z ) F_1(z) F1(z)与 F 2 ( z ) F_2(z) F2(z)收敛域的相交部分。
2、移位(移序)特性
双边z变换的移位:
若 f ( k ) ← F ( z ) , α < ∣ z ∣ < β f(k) \leftarrow F(z), \alpha<|z|<\beta f(k)←F(z),α<∣z∣<β,则对整数 m > 0 m\gt 0 m>0:
f ( k ± m ) ← → z ± m F ( z ) , α < ∣ z ∣ < β f(k \pm m) \leftarrow \rightarrow z^{\pm m} F(z), \quad \alpha<|z|<\beta f(k±m)←→z±mF(z),α<∣z∣<β
单边z变换的移位:
f ( k − m ) ← → z − m F ( z ) + ∑ k = 0 m − 1 f ( k − m ) z − k f(k-m) \leftarrow \rightarrow z^{-m} F(z)+\sum_{k=0}^{m-1} f(k-m) z^{-k} f(k−m)←→z−mF(z)+k=0∑m−1f(k−m)z−k
右移,原来在负轴的部分移位到正轴,所以需要加 ∑ k = 0 m − 1 f ( k − m ) z − k \sum_{k=0}^{m-1} f(k-m) z^{-k} ∑k=0m−1f(k−m)z−k
f ( k + m ) ← → z m F ( z ) − ∑ k = 0 m − 1 f ( k ) z m − k f(k+m) \leftarrow \rightarrow z^{m} F(z)-\sum_{k=0}^{m-1} f(k) z^{m-k} f(k+m)←→zmF(z)−k=0∑m−1f(k)zm−k
左移,原来在正轴的部分移位到负轴,所以需要减 ∑ k = 0 m − 1 f ( k ) z m − k \sum_{k=0}^{m-1} f(k) z^{m-k} ∑k=0m−1f(k)zm−k
特例:若 f ( k ) f(k) f(k)为因果序列(负轴信号值为0),则
f ( k − m ) ← → z − m F ( z ) f(k-m) \leftarrow \rightarrow z^{-m} F(z) f(k−m)←→z−mF(z)
即:
f ( k − m ) ε ( k − m ) ← → z − m F ( z ) f(k-m) \varepsilon(k-m) \leftarrow \rightarrow z^{-m} F(z) f(k−m)ε(k−m)←→z−mF(z)
3、 k k k域反转(仅适用双边z变换)
设 f ( k ) ↔ F ( z ) , α < ∣ z ∣ < β f(k) \leftrightarrow F(z), \quad \alpha<|z|<\beta f(k)↔F(z),α<∣z∣<β
则 f ( − k ) ↔ F ( z − 1 ) , 1 β < ∣ z ∣ < 1 α f(-k) \leftrightarrow F\left(z^{-1}\right), \quad \frac{1}{\beta}<|z|<\frac{1}{\alpha} f(−k)↔F(z−1),β1<∣z∣<α1
3.2 z域尺度特性、微分
1、z域尺度变换:序列乘 a k , a ≠ 0 a^k,a\not=0 ak,a=0
设 f ( k ) ↔ F ( z ) , α < ∣ z ∣ < β f(k) \leftrightarrow F(z), \quad \alpha<|z \mid<\beta f(k)↔F(z),α<∣z∣<β,且有常数 a a a,则
a k f ( k ) ↔ F ( z a ) , ∣ a ∣ α < ∣ z ∣ < ∣ a ∣ β a^{k} f(k) \leftrightarrow F\left(\frac{z}{a}\right),|a| \alpha<|z|<|a| \beta akf(k)↔F(az),∣a∣α<∣z∣<∣a∣β
2、序列乘 k k k(z域微分)
设 f ( k ) ↔ F ( z ) , α < ∣ z ∣ < β f(k) \leftrightarrow F(z), \quad \alpha<|z|<\beta f(k)↔F(z),α<∣z∣<β
则
k f ( k ) ↔ ( − z ) d d z F ( z ) k f(k) \leftrightarrow(-z) \frac{d}{d z} F(z) kf(k)↔(−z)dzdF(z)
k 2 f ( k ) ↔ ( − z ) d d z [ ( − z ) d d z F ( z ) ] k^{2} f(k) \leftrightarrow(-z) \frac{d}{d z}\left[(-z) \frac{d}{d z} F(z)\right] k2f(k)↔(−z)dzd[(−z)dzdF(z)]
k m f ( k ) ↔ ( − z ) d d z ( ⋯ ( − z ) d d z ( ( − z ) d d z F ( z ) ) ⋯ ) ⏟ m 次 , α < ∣ z ∣ < β k^{m} f(k) \leftrightarrow \underbrace{(-z) \frac{d}{d z}\left(\cdots(-z) \frac{d}{d z}\left((-z) \frac{d}{d z} F(z)\right) \cdots\right)}_{m \text { 次 }}, \quad \alpha<|z|<\beta kmf(k)↔m 次
(−z)dzd(⋯(−z)dzd((−z)dzdF(z))⋯),α<∣z∣<β
e j β e^{j\beta} ejβ看作一个整体, e − j β e^{-j\beta} e−jβ也看作一个整体。
因为是单边z变换: ( k + 1 ) ε ( k + 1 ) = ( k + 1 ) ε ( k ) (k+1) \varepsilon(k+1)=(k+1) \varepsilon(k) (k+1)ε(k+1)=(k+1)ε(k)
3.3 时域卷积
设:
f 1 ( k ) ↔ F 1 ( z ) , α 1 < ∣ z ∣ < β 1 f_{1}(k) \leftrightarrow F_{1}(z), \quad \alpha_{1}<|z|<\beta_{1} f1(k)↔F1(z),α1<∣z∣<β1
f 2 ( k ) ↔ F 2 ( z ) , α 2 < ∣ z ∣ < β 2 f_{2}(k) \leftrightarrow F_{2}(z), \quad \alpha_{2}<|z|<\beta_{2} f2(k)↔F2(z),α2<∣z∣<β2
则
f 1 ( k ) ∗ f 2 ( k ) ↔ F 1 ( z ) ⋅ F 2 ( z ) , max ( α 1 , α 2 ) < z ∣ < min ( β 1 , β 2 ) f_{1}(k) * f_{2}(k) \leftrightarrow F_{1}(z) \cdot F_{2}(z), \max \left(\alpha_{1}, \alpha_{2}\right)<z \mid<\min \left(\beta_{1}, \beta_{2}\right) f1(k)∗f2(k)↔F1(z)⋅F2(z),max(α1,α2)<z∣<min(β1,β2)
说明:
(1) 收敛域一般为 F 1 ( z ) F_1(z) F1(z)与 F 2 ( z ) F_2(z) F2(z)收敛域的相交部分;
(2) 对单边z变换,要求: f 1 ( k ) f_1(k) f1(k)、 f 2 ( k ) f_2(k) f2(k)为因果序列
画图,可知 k ε ( k − 1 ) = k ε ( k ) k\varepsilon(k-1)=k\varepsilon(k) kε(k−1)=kε(k)
3.4 部分和
若 f ( k ) ← → F ( z ) , α < ∣ z ∣ < β f(k) \leftarrow \rightarrow F(z), \alpha<|z|<\beta f(k)←→F(z),α<∣z∣<β
∑ i = − ∞ k f ( i ) ← → z z − 1 F ( z ) , max ( α , 1 ) < ∣ z ∣ < β \sum_{i=-\infty}^{k} f(i) \leftarrow \rightarrow \frac{z}{z-1} F(z), \max (\alpha, 1)<|z|<\beta i=−∞∑kf(i)←→z−1zF(z),max(α,1)<∣z∣<β
证明:时域卷积对应频域乘积
f ( k ) ∗ ε ( k ) = ∑ i = − ∞ ∞ f ( i ) ε ( k − i ) = ∑ i = − ∞ k f ( i ) ⟷ z z − 1 F ( z ) f(k)^{*} \varepsilon(k)=\sum_{i=-\infty}^{\infty} f(i) \varepsilon(k-i)=\sum_{i=-\infty}^{k} f(i) \longleftrightarrow \frac{z}{z-1} F(z) f(k)∗ε(k)=i=−∞∑∞f(i)ε(k−i)=i=−∞∑kf(i)⟷z−1zF(z)
3.5 初值定理和终值定理
初值定理适用于右边序列,即适用于 k < M k\lt M k<M( M M M为整数)时 f ( k ) = 0 f(k)=0 f(k)=0的序列。由象函数直接求序列的初值 f ( M ) f(M) f(M), f ( M + 1 ) f(M+1) f(M+1), … 而不必求得原序列。
1、初值定理:
如果序列在 k < M k<M k<M时, f ( k ) = 0 , f ( k ) ← → F ( z ) , α < ∣ z ∣ < ∞ f(k)=0, \quad f(k) \leftarrow \rightarrow F(z), \quad \alpha<|z|<\infty f(k)=0,f(k)←→F(z),α<∣z∣<∞
则序列的初值
f ( M ) = lim z → ∞ z M F ( z ) f(M)=\lim _{z \rightarrow \infty} z^{M} F(z) f(M)=z→∞limzMF(z)
对因果序列 f ( k ) f(k) f(k), M = 0 M=0 M=0
f ( 0 ) = lim z → ∞ F ( z ) f(0)=\lim _{z \rightarrow \infty} F(z) f(0)=z→∞limF(z)
z M F ( z ) = f ( M ) + f ( M + 1 ) z − 1 + f ( M + 2 ) z − 2 + … z^{M} F(z)=f(M)+f(M+1) z^{-1}+f(M+2) z^{-2}+\ldots zMF(z)=f(M)+f(M+1)z−1+f(M+2)z−2+…
上式取 z → ∞ z→∞ z→∞,得
f ( M ) = lim z → ∞ z M F ( z ) f(M)=\lim _{z \rightarrow \infty} z^{M} F(z) f(M)=z→∞limzMF(z)
2、终值定理:
如果序列存在终值,即:
f ( ∞ ) = lim k → ∞ f ( k ) f(\infty)=\lim _{k \rightarrow \infty} f(k) f(∞)=k→∞limf(k)
则序列的终值
f ( ∞ ) = lim z → 1 z − 1 z F ( z ) = lim z → 1 ( z − 1 ) F ( z ) f(\infty)=\lim _{z \rightarrow 1} \frac{z-1}{z} F(z)=\lim _{z \rightarrow 1}(z-1) F(z) f(∞)=z→1limzz−1F(z)=z→1lim(z−1)F(z)
注意:收敛域要求含单位圆。
4 逆z变换:幂级数和部分分式展开
F ( z ) F(z) F(z)的逆z变换
f ( k ) = 1 2 π j ∮ c F ( z ) z k − 1 d z , − ∞ < k < ∞ f(k)=\frac{1}{2 \pi j} \oint_{c} F(z) z^{k-1} d z, \quad-\infty<k<\infty f(k)=2πj1∮cF(z)zk−1dz,−∞<k<∞
z 逆变换的计算方法:
(1)反演积分法(留数法);
(2)幂级数展开法;(有局限性)
(3)部分分式展开法;
(4)用 z z z 变换性质求逆 z z z 变换。(组合使用)
一般而言,双边序列 f ( k ) f(k) f(k)可分解为因果序列 f 1 ( k ) f_1(k) f1(k)和反因果序列 f 2 ( k ) f_2(k) f2(k)两部分,即
f ( k ) = f 2 ( k ) + f 1 ( k ) = f ( k ) ε ( − k − 1 ) + f ( k ) ε ( k ) f(k)=f_{2}(k)+f_{1}(k)=f(k) \varepsilon(-k-1)+f(k) \varepsilon(k) f(k)=f2(k)+f1(k)=f(k)ε(−k−1)+f(k)ε(k)
其中
F 1 ( z ) = Z [ f ( k ) ε ( k ) ] = ∑ k = 0 ∞ f ( k ) z − k , ∣ z ∣ > α F_{1}(z)=Z[f(k) \varepsilon(k)]=\sum_{k=0}^{\infty} f(k) z^{-k}, \quad|z|>\alpha F1(z)=Z[f(k)ε(k)]=k=0∑∞f(k)z−k,∣z∣>α
F 2 ( z ) = Z [ f ( k ) ε ( − k − 1 ) ] = ∑ k = − ∞ − 1 f ( k ) z − k , ∣ z ∣ < β F_{2}(z)=Z[f(k) \varepsilon(-k-1)]=\sum_{k=-\infty}^{-1} f(k) z^{-k}, \quad|z|<\beta F2(z)=Z[f(k)ε(−k−1)]=k=−∞∑−1f(k)z−k,∣z∣<β
已知象函数 F ( z ) F(z) F(z)时,根据给定的收敛域不难由 F ( z ) F(z) F(z)分解为 F 1 ( z ) F_1(z) F1(z)和 F 2 ( z ) F_2(z) F2(z),分别求对应的原序列 f 1 ( k ) f_1(k) f1(k)和 f 2 ( k ) f_2(k) f2(k),根据线性性质,将两者相加原序列 f ( k ) f(k) f(k)
1、幂级数展开法
根据 z z z变换的定义,因果序列和反因果序列的象函数分别是 z − 1 z^{-1} z−1和 z z z的幂级数; 其系数就是相应的序列值。
2、部分分式展开法
F ( z ) = B ( z ) A ( z ) = b m z m + b m − 1 z m − 1 + … . + b 1 z + b 0 z n + a n − 1 z n − 1 + … . + a 1 z + a 0 , m ≤ n F(z)=\frac{B(z)}{A(z)}=\frac{b_{m} z^{m}+b_{m-1} z^{m-1}+\ldots .+b_{1} z+b_{0}}{z^{n}+a_{n-1} z^{n-1}+\ldots .+a_{1} z+a_{0}}, m \leq n F(z)=A(z)B(z)=zn+an−1zn−1+….+a1z+a0bmzm+bm−1zm−1+….+b1z+b0,m≤n
(1) F ( z ) F(z) F(z)均为单极点,且不为0
F ( z ) z = K 0 z + K 1 z − z 1 + … . + K n z − z n \frac{F(z)}{z}=\frac{K_{0}}{z}+\frac{K_{1}}{z-z_{1}}+\ldots .+\frac{K_{n}}{z-z_{n}} zF(z)=zK0+z−z1K1+….+z−znKn
F ( z ) z \frac{F(z)}{z} zF(z)除以 z z z原因:
z z − a ↔ a k ε ( k ) \frac{z}{z-a}\leftrightarrow a^k\varepsilon(k) z−az↔akε(k)
而部分分式展开得到的分式上没有 z z z
其中
K i = ( z − z i ) F ( z ) z ∣ z = z i K_{i}=\left.\left(z-z_{i}\right) \frac{F(z)}{z}\right|_{z=z_{i}} Ki=(z−zi)zF(z)∣∣∣∣z=zi
所以:
F ( z ) = K 0 + ∑ i = 1 n K i z z − z i F(z)=K_{0}+\sum_{i=1}^{n} \frac{K_{i} z}{z-z_{i}} F(z)=K0+i=1∑nz−ziKiz
根据收敛域,将上式划分为 F 1 ( z ) ( ∣ z ∣ > α ) F_{1}(z)(|z|>\alpha) F1(z)(∣z∣>α)和 F 2 ( z ) ( ∣ z ∣ < β ) F_{2}(z)(|z|<\beta) F2(z)(∣z∣<β),由如下已知变换对,来求原函数。
δ ( k ) ← → 1 \delta(k) \leftarrow \rightarrow 1 δ(k)←→1 a k ε ( k ) ← → z z − a , ∣ z ∣ > ∣ a ∣ a^{k} \varepsilon(k) \leftarrow \rightarrow \frac{z}{z-a},|z|>|a| akε(k)←→z−az,∣z∣>∣a∣
− a k ε ( − k − 1 ) ← → z z − a , ∣ z ∣ < ∣ a ∣ -a^{k} \varepsilon(-k-1) \leftarrow \rightarrow \frac{z}{z-a},|z|<|a| −akε(−k−1)←→z−az,∣z∣<∣a∣
如果是单边的,则只考虑(1)
(3) F ( z ) F(z) F(z)有重极点
F ( z ) F(z) F(z)展开式中含 z ( z − a ) r \frac{z}{(z-a)^{r}} (z−a)rz项( r > 1 r\gt 1 r>1),则逆变换为:
若 ∣ z ∣ > a |z|\gt a ∣z∣>a ,对应原序列为因果序列:
k ( k − 1 ) … . . ( k − r + 2 ) ( r − 1 ) ! a k − r + 1 ε ( k ) \frac{k(k-1) \ldots . .(k-r+2)}{(r-1) !} a^{k-r+1} \varepsilon(k) (r−1)!k(k−1)…..(k−r+2)ak−r+1ε(k)
以 ∣ z ∣ > a |z|\gt a ∣z∣>a为例:
推导记忆:
Z [ a k ε ( k ) ] = z z − a \mathscr{Z}\mathscr{[ a ^ { k } \varepsilon ( k ) ]}=\frac{z}{z-a} Z[akε(k)]=z−az
两边对 a a a求导得:
Z [ k a k − 1 ε ( k ) ] = z ( z − a ) 2 \mathscr{Z}\mathscr{[ k a ^ { k – 1 } \varepsilon ( k ) ]}=\frac{z}{(z-a)^{2}} Z[kak−1ε(k)]=(z−a)2z
再对 a a a求导得
Z [ k ( k − 1 ) a k − 2 ε ( k ) ] = 2 z ( z − a ) 3 \mathscr{Z}\left[k(k-1) a^{k-2} \varepsilon(k)\right]=\frac{2 z}{(z-a)^{3}} Z[k(k−1)ak−2ε(k)]=(z−a)32z
Z [ 1 2 k ( k − 1 ) a k − 2 ε ( k ) ] = z ( z − a ) 3 \mathscr{Z}\left[\frac{1}{2} k(k-1) a^{k-2} \varepsilon(k)\right]=\frac{z}{(z-a)^{3}} Z[21k(k−1)ak−2ε(k)]=(z−a)3z
3、用性质求逆z变换
5 z变换与拉普拉斯变换的关系
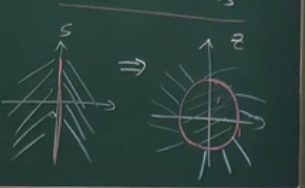
1、Z平面与S平面的映射关系
z = e s T s = 1 T ln z z=e^{sT} \quad s=\frac{1}{T}\ln z z=esTs=T1lnz
式中 T T T是序列的时间间隔,重复频率 ω s = 2 π T \omega_{s}=\frac{2 \pi}{T} ωs=T2π
为了说明s与z的映射关系,将s表示成直角坐标形式,而把 z 表示成极坐标形式,即
s = σ + j ω z = r e j θ s=\sigma+j \omega \quad z=r e^{j \theta} s=σ+jωz=rejθ
z = r e j θ = e ( σ + j ω ) T = e σ T e j ω T z=r e^{j \theta}=e^{(\sigma+j \omega) T}=e^{\sigma T} e^{j \omega T} z=rejθ=e(σ+jω)T=eσTejωT
于是,得到
r = e σ T = e 2 π σ ω s θ = ω T = 2 π ω ω S r=e^{\sigma T}=e^{\frac{2 \pi \sigma}{\omega_{s}}} \quad \theta=\omega T=2 \pi \frac{\omega}{\omega_{S}} r=eσT=eωs2πσθ=ωT=2πωSω
上式表明s平面与z平面有如下的映射关系:
(1) s平面上的虚轴( σ = 0 , ω = ω , s = j ω σ=0,ω=ω,s=jω σ=0,ω=ω,s=jω)映射到z平面是单位圆 r = 1 r=1 r=1,其右半平面 σ > 0 σ>0 σ>0映射到 z平面的单位圆外 r > 1 r>1 r>1,而左半平面映射到 z平面的单位圆内 r < 1 r<1 r<1。
s = σ + j ω z = r e j θ s=\sigma+j \omega \quad z=r e^{j \theta} s=σ+jωz=rejθ
(2) s平面的实轴( σ = σ , ω = 0 , s = σ σ=σ,ω=0,s=σ σ=σ,ω=0,s=σ) 映射到z平面的正实轴;原点( σ = 0 , ω = 0 , s = 0 σ=0,ω=0,s=0 σ=0,ω=0,s=0)映射到z平面的正实轴上一点( r = 1 , θ = 0 r=1,θ=0 r=1,θ=0) 。
(3) 由于 e j θ e^{jθ} ejθ 是以 ω s ω_s ωs为周期的周期函数,因此在s平面沿虚轴移动对应于z平面上沿单位圆周期旋转,每平移 ω s ωs ωs,则沿单位圆转一圈。所以 s ∼ z s\sim z s∼z映射并不是单值的
2、s变换与z变换的转换公式
z z z变换的定义式是通过理想取样信号的拉普拉斯变换引出的,由此,离散序列的 z z z变换和理想取样信号的拉普拉斯变换之间具有如下关系:
F ( z ) ∣ z = e s T = F s ( s ) \left.F(z)\right|_{z=e^{s T}}=F_{s}(s) F(z)∣z=esT=Fs(s)
( F s ( s ) F_{s}(s) Fs(s)下标 s s s表示采样信号的拉普拉斯变换。)
表明: z变换式中令 z = e s T z=e^{sT} z=esT,则变换式就成为相应的理想取样信号的拉普拉斯变换。
如果进一步地,令拉普拉斯变换中的变量 s = j ω s=jω s=jω,则
F ( z ) ∣ z = e j ω T = F s ( j ω ) \left.F(z)\right|_{z=e^{j \omega T}}=F_{s}(j \omega) F(z)∣z=ejωT=Fs(jω)
上式变为与序列相对应的理想取样信号的傅里叶变换。
讨论:若连续信号 f ( t ) f(t) f(t)由 N N N项指数信号相加而成(单极点):
f ( t ) = f 1 ( t ) + f 2 ( t ) + … + f N ( t ) = ∑ i = 1 N f i ( t ) = ∑ i = 1 N A i e p i t ε ( t ) f(t)=f_{1}(t)+f_{2}(t)+\ldots+f_{N}(t)=\sum_{i=1}^{N} f_{i}(t)=\sum_{i=1}^{N} A_{i} e^{p_{i} t} \varepsilon(t) f(t)=f1(t)+f2(t)+…+fN(t)=i=1∑Nfi(t)=i=1∑NAiepitε(t)
容易求得,其拉普拉斯变换为:
F ( s ) = ∑ i = 1 N A i s − p i F(s)=\sum_{i=1}^{N} \frac{A_{i}}{s-p_{i}} F(s)=i=1∑Ns−piAi
对应的采样离散序列 f ( k ) f(k) f(k)由 N N N项指数序列相加而成
它的z变换为
F ( z ) = ∑ i = 1 N A i z z − e p i T F(z)=\sum_{i=1}^{N} \frac{A_{i} z}{z-e^{p_{i} T}} F(z)=i=1∑Nz−epiTAiz
F ( s ) = ∑ i = 1 N A i s − p i F(s)=\sum_{i=1}^{N} \frac{A_{i}}{s-p_{i}} F(s)=i=1∑Ns−piAi F ( z ) = ∑ i = 1 N A i z z − e p i T F(z)=\sum_{i=1}^{N} \frac{A_{i} z}{z-e^{p_{i} T}} F(z)=i=1∑Nz−epiTAiz
结论:如果 F ( s ) F(s) F(s)有 N N N个单极点 p i p_i pi,则相应的z变换即为 F ( z ) F(z) F(z)。
中国大学MOOC:信号与系统 ,西安电子科技大学,郭宝龙,朱娟娟
今天的文章z变换在信号与系统中的应用_对一个典型二阶系统输入一脉冲信号分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/81974.html