巴什博弈必胜策略简单点说_博弈论需要什么数学基础

博弈论基础

    博弈论又被称为对策论(Game Theory)，既是现代数学的一个新分支，也是运筹学的一个重要学科。博弈论主要研究公式化了的激励结构间的相互作用，是研究具有斗争或竞争性质现象的数学理论和方法。博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。

引入：囚徒困境

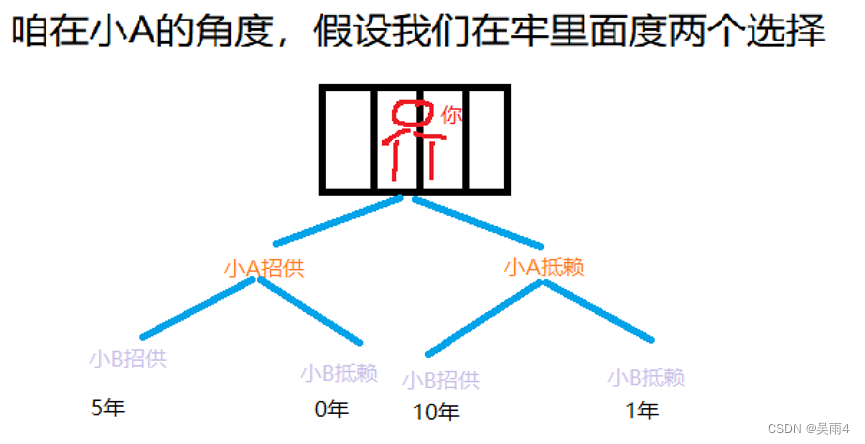
    囚徒困境的故事讲的是,两个嫌疑犯小A、小B作案后被警察抓住,分别关在不同的屋子里接受审讯。警察知道两人有罪,但缺乏足够的证据。警察告诉每个人:如果两人都抵赖,各判刑一年;如果两人都坦白,各判五年;如果两人中一个坦白而另一个抵赖,坦白的放出去,抵赖的判十年。

于是,每个囚徒都面临两种选择:坦白或抵赖。

    在不和小B商量的情况下，作为小A的你是选择招供坐牢5年或0年，还是会选择抵赖坐牢10年或1年呢？

一般的人都会选着保险一点的招供吧。

    反观小B，也一定会做出同样的选择，也就是招供。换句话说，只要两名囚徒都是自私且理性的，那么双方都会同时选择招供，结果就是双方各判5年。

    在这个场景中，双方都无法单方面改变自己的博弈策略（单方面改变只会让自己蒙受损失），使得局面进入了一个微妙而又稳定的平衡，这个平衡被称为纳什均衡。

    在现实中,也有很多类似的现象,比如家长给孩子报越来越多的课外班,比如高三考生备战高考,卷起来了啊.从局外人看来,许多竞争都是显而易见双输的局面,但是我们没有办法,因为我们都是参与博弈的“囚徒”。

ICG博弈

所讨论的博弈问题满足以下条件：

    玩家只有两个人，轮流做出决策。

    游戏的状态集有限，保证游戏在有限步后结束，这样必然会产生不能操作者，其输。

    对任何一种局面，胜负只决定于局面本身，而与轮到哪位选手无关。

取石子游戏：取石子游戏是一个古老的博弈游戏，发源于中国，它是组合数学领域的一个经典问题。它有许多不同的玩法，基本上是两个玩家，玩的形式是轮流抓石子，胜利的标准是抓走最后的石子。玩家设定： 先取石子的是玩家A（先手A），后取石子的是玩家B（后手B）。

经典的三种玩法

一、巴什博奕(Bash Game)

二、尼姆博奕(Nimm Game)

三、威佐夫博奕(Wythoff Game)

（一）巴什博弈

1堆n个石子每次最多取m个、至少取1个

Case 1:如果n=m+1，那么由于一次最多只能取m个，所以，无论先取者拿走多少个，后取者都能够一次拿走剩余的物品，后者取胜。

Case 2:n=(m+1)*r+s，(r为任意自然数，s≤m),那么先取者要拿走s个物品，如果后者拿走k(1≤k≤m)个，那么先取者再拿走m+1-k个，结果剩下(m+1)(r-1)个，以后保持这样的取法，那么先取者肯定获胜。

Case 3:n=r*(m+1)，先手拿走k(1≤k≤m)个，那么后手再拿走m+1-k个，结果剩下(m+1)(r-1)个，以后保持这样的取法，则后手胜，先手必败。

总之，要保持给对手留下（m+1）的倍数，就能最后获胜。

术语:正经人称(m+1)的局面为奇异局势

变相的玩法

两个人轮流报数，每次至少报一个，最多报十个，谁能报到100者胜。（等价于从一堆100个石子中取石子，最后取完的胜）

例题：2368 — Buttons (poj.org)

题面：

      题面意思：有一堆k个的石头，每人轮流拿1,2，..L个石头，数据范围是3 <= K <= 100 000 000 ，2 <= L < K。输入k的值，要求输出最小的L，使得后者胜。

在理解了巴什博弈之后来看这题还是思路比较清晰的，首先想让后手胜，就必须把（1+L）的局面留给先手。这题没问我们谁会赢，问的是后手要赢的最小L值为多少。那我们就找到能被k整除的最小大于2的因数，之后减1输出就是答案了。

于是有了以下代码注意下（poj用不了万能头文件，编译器要求有点严格。）：

//#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int N=100005;
ll n;//石子数量
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    ll i;
    for(i=2;i<n;i++)//依次找最小的因子
    {
        if(n%(i+1)==0)
        {
            cout<<i<<endl;
            break;
        }
    }
    if(i==n) cout<<0<<endl;//找不到的情况下输出0
    return 0;
}

 就是说数据范围1e8，就超时快乐，TEL了哈哈哈哈哈哈。由于循环2~n，时间复杂度是O(n)。

    再有一个新的思路就是，遍历一遍所有的n的因数，存起来，在输出最小大于等于3的因数减一。一下代码时间复杂度为O(log n)。AC快乐。

//#include<bits/stdc++.h>
#include<algorithm>
#include<math.h>
#include<iostream>
#include<stdio.h>
using namespace std;
typedef long long ll;
const int N=100005;
ll n,a[N];//n为石头总数，a[i]存n的因数
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    int temp=0;
    for(int i=1;i*i<=n;i++)
    {
        if(n%i==0&&i*i!=n) a[temp++]=i,a[temp++]=n/i;
        //注意要区别开类似n=4时，因数为1,2,4.而不是1,2,2,4的情况
        else if(n%i==0&&i*i==n) a[temp++]=i;
    }
    sort(a,a+temp);//从小到大排序一下
    for(int i=0;i<temp;i++)
    {
        if(a[i]>=3)//找到最小大于等于3的因数，减一输出
        {
            cout<<a[i]-1<<endl;
            break;
        }
    }
    return 0;
}

（二）尼姆博弈

有n堆石子，每堆石子的数量是a1,a2,a3……，二个人依次从这些石子堆中的一个拿取任意的石子，至少一个，最后一个拿光石子的人胜利

n=1: 先手全拿，先手必胜。

n=2:有两种情况，一种可能相同，一种情况一堆比另一堆少（多）

        (m,m) 按照“有一学一，照猫画猫”法，先手必输。

        (m,M)先手先从多的一堆中拿出(M-m)个，此时后手面对(m,m)的局面先手必胜。

术语:正经人称(m,m)的局面为奇异局势

n=3:(m,m,M)先手必胜局，先手可以先拿M,之后变成了(m,m,0)的局面，是不是很熟悉~

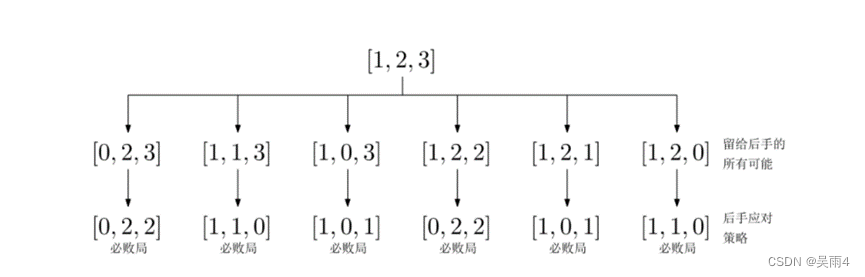
 (a1,a2,a3)的话，举个例子(1,2,3),先手取完之后可能的局面为(0,2,3),(1,1,3),(1,0,3),(1,2,2),(1,2,1),(1,2,0)都是之前讲过的，情况如下：

前人告诉我们的规律是：异或的结果均为0

获胜情况的讨论

面对异或结果为0的玩家必输。

结果不为0，则玩家有获胜的取法。

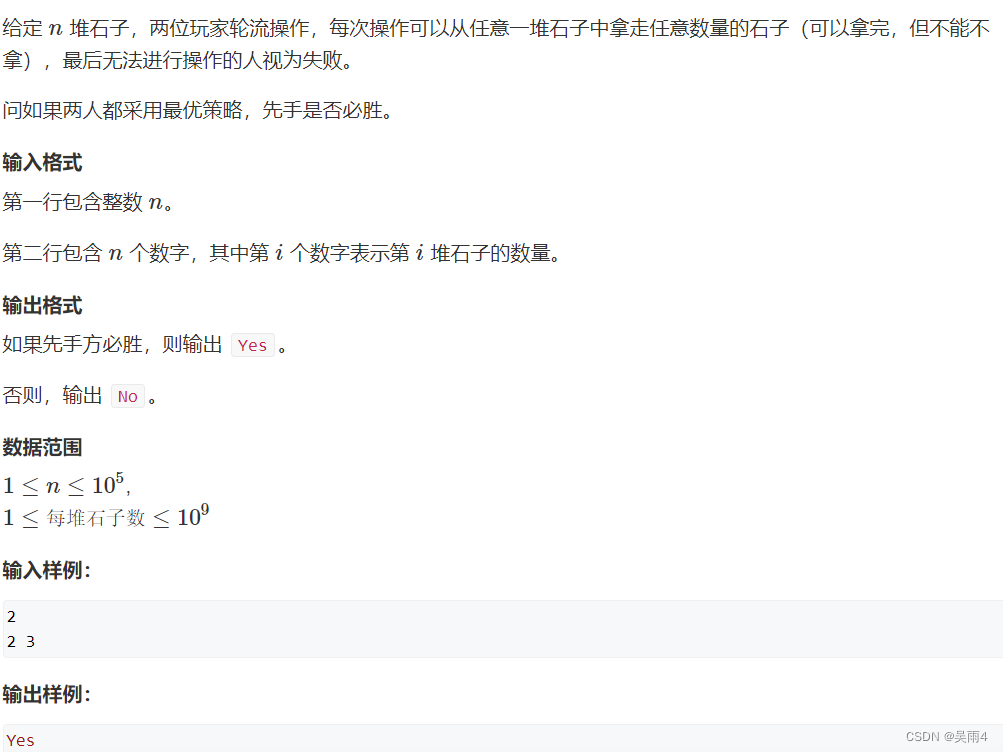
例题：891. Nim游戏 – AcWing题库

 题面：

看懂了尼姆博奕，这个题目就是分分钟AC咯。

上代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100005;
ll n,a[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
    int ans=a[0];
    for(int i=1;i<n;i++) ans^=a[i];//^就是做异或运算
    if(ans==0) cout<<"No"<<endl;
    else cout<<"Yes"<<endl;
    return 0;
}

(三)威佐夫博弈

有两堆各若干个物品，两个人轮流从任一堆取至少一个或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

举一个例子:局势是(1,2)，先手有四种取法，动动你聪明的脑子就会发现无论先手怎么取，后手都能胜利，也就是说(1,2)是奇异局势。

没脑子的人来看看分析咯：

先手从第一堆里面拿1个，后者拿光后面的2个，后者胜。

先手从第一堆和第二堆里面同时拿1个，后者只能拿走第二堆剩下的1个，后者胜。

先手从第二堆里面拿2个，后手拿走第一堆的1个，后者胜.

先手从第二堆里面拿1个，后手从第一堆和第二堆里面同时拿走1个，后者胜。

假设现在的局势是（3,5)：

（1）先手在“3”中取1个，后手就可以在“5”中取走4个，这样就变成了（1，2）的局势

（2）先手在“3”中取2个，后手就可以在 “5” 中取走3个，这样也变成了（1,2）的局势

（3）先手在“5”中取1个，后手就在 “3”和“5” 中各取走2个，这样成了（1，2）的局势

（4）先手在”5”中取2个,后手就在 “3”和”5”中各取走3个,这样变成了(0，0)的局势，先手输

（5）先手在“5”中取3个，后手就在 “3”和“5” 中各取走1个，也变成了（1，2）的局势

（6）先手在“5”中取4个，后手在“3”中取走1个，还是（1，2）的局势

我们可以来找找那些先手必输局势的规律（奇异局势）

• 第一种（0，0）
• 第二种（1，2）
• 第三种（3，5）
• 第四种  (4 ，7）
• 第五种（6，10）
• 第六种  (8，13）              
• 第七种  (9 ，15）
• 第八种  (11 ，18）
• 第n种（a，b）

我们会发现他们的差值是递增的，分别是0,1,2,3,4,5,6,7……n

还有一个规律(正常人都发现不了):a=(b-a)*1.618向下取整

 就是：a = int(b – a)*1.618

注：这里的int是强制类型转换，注意这不是简单的四舍五入，假如后面的值是3.9，转换以后得到的不是4而是3，也就是说强制int类型转换得到的是不大于这个数值的最大整数。

有些题目要求精度较高，我们可以用下述式子来表示这个值:

1.618 = (sqrt(5.0) + 1) / 2   

头文件：include<math.h>

例题：1067 — 取石子游戏 (poj.org)

题面：

 代码：

//#include<bits/stdc++.h>
#include<algorithm>
#include<math.h>
#include<iostream>
#include<stdio.h>
using namespace std;
typedef long long ll;
const int N=100005;
ll a,b;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    while(cin>>a>>b)//多组输入！！！
    {
        double flag= (sqrt(5.0) + 1) / 2.0;//精度高一些用double来存1.618
        if(a>b) swap(a,b);//保证b要比a大，后面有用到b-a
        if(a==int((b-a)*flag))cout<<0<<endl;//先手面对奇异局势必输
        else cout<<1<<endl;
    }

    return 0;
}

今天的文章巴什博弈必胜策略简单点说_博弈论需要什么数学基础分享到此就结束了，感谢您的阅读。