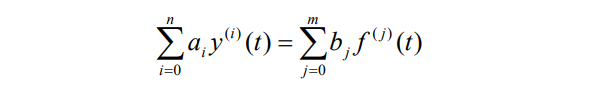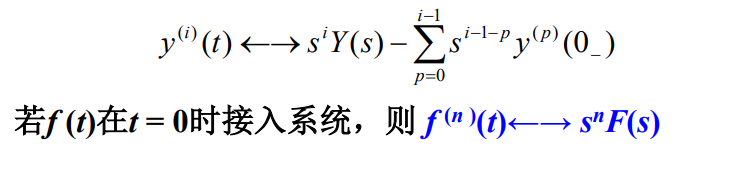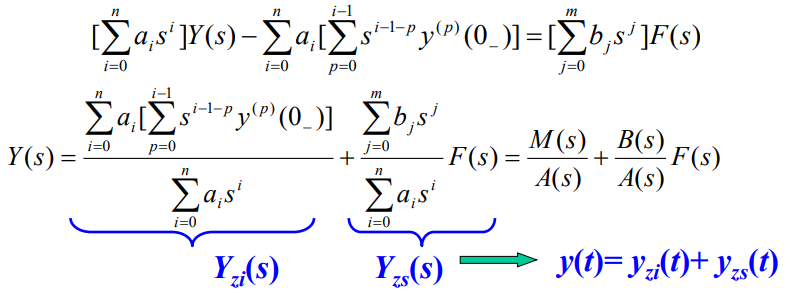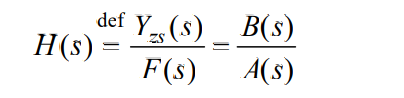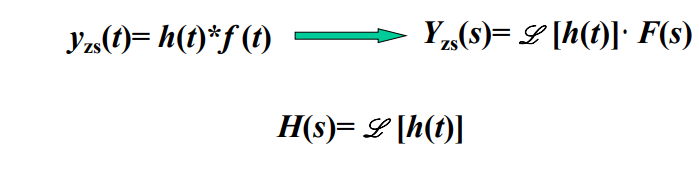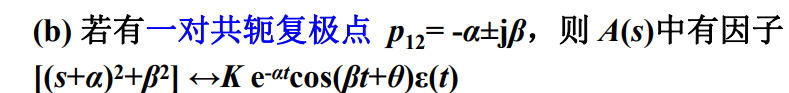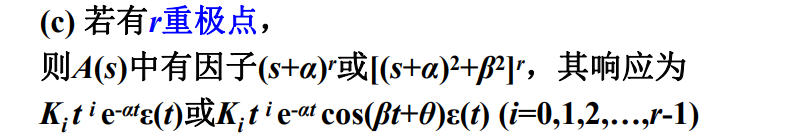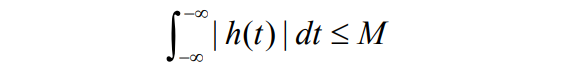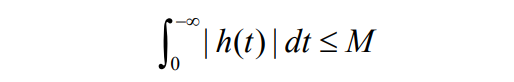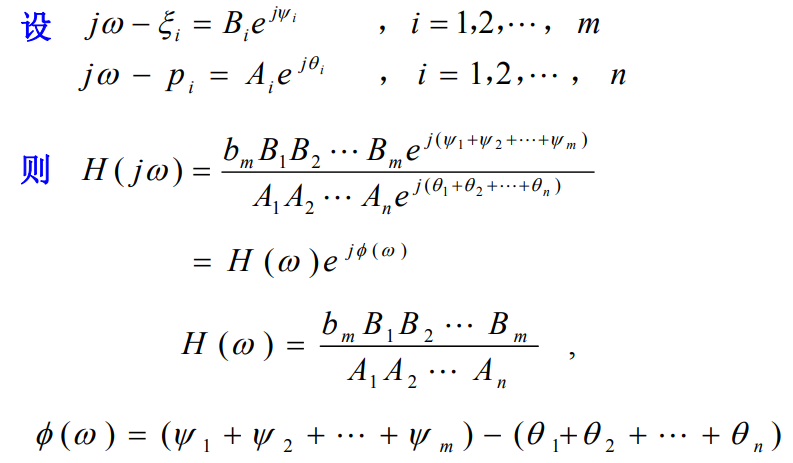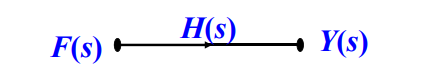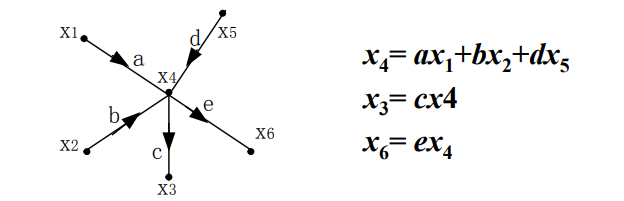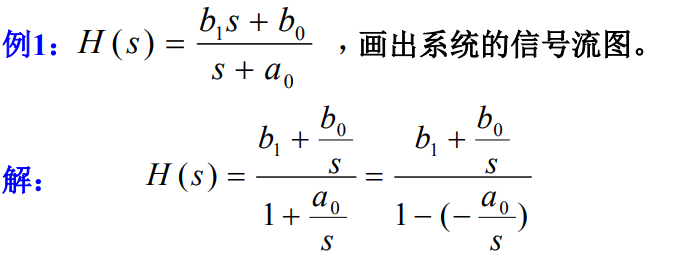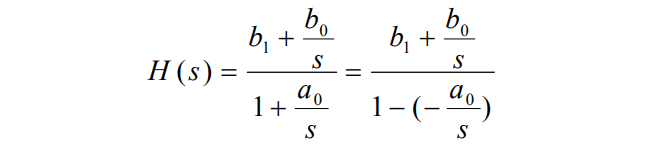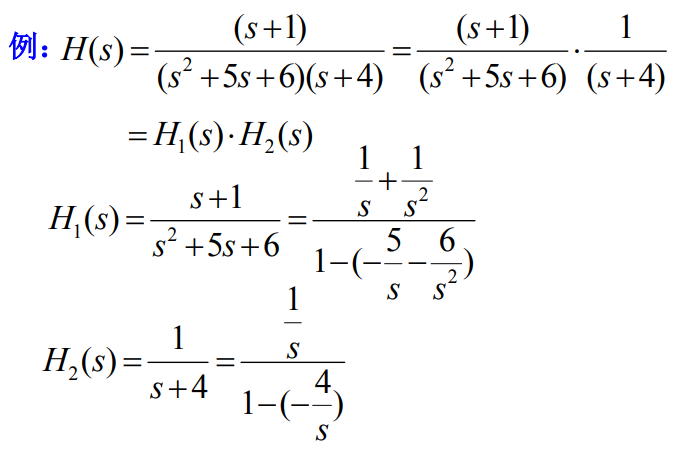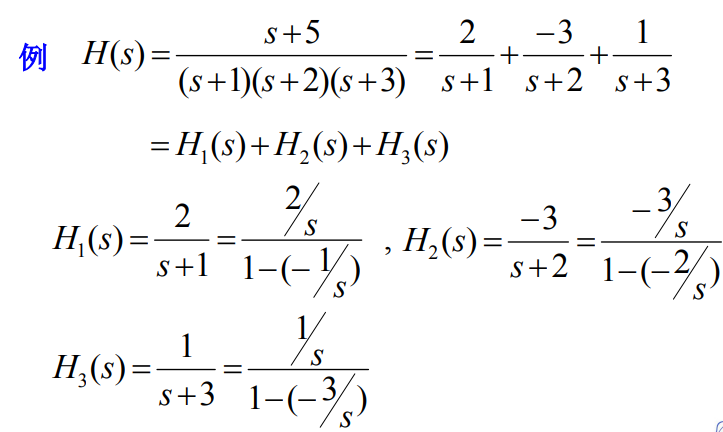周期信号的拉普拉斯变换咋求_周期信号的拉普拉斯变换咋求

s域分析

1 微分方程的变换解

问题：如何用拉普拉斯变换求如下n阶系统的微分方程？

系统的初始状态为$y(0-),y^{(1)}(0-),\dots ,y^{(\mathrm{n}-1)}(0-)$

方法是利用拉普拉斯变换微分特性：

微分方程两边进行拉氏变换：

$$s^{2}Y(s)-sy(0_{-})-y^{\prime }(0_{-})+5(Y(s)-y(0_{-}))+6Y(s)=2sF(s)+6F(s)$$

2 连续系统函数$H(s)$的定义和求解

系统函数$H(s)$定义：

说明：系统函数只与系统的结构、元件参数有关，与激励、初始状态无关。

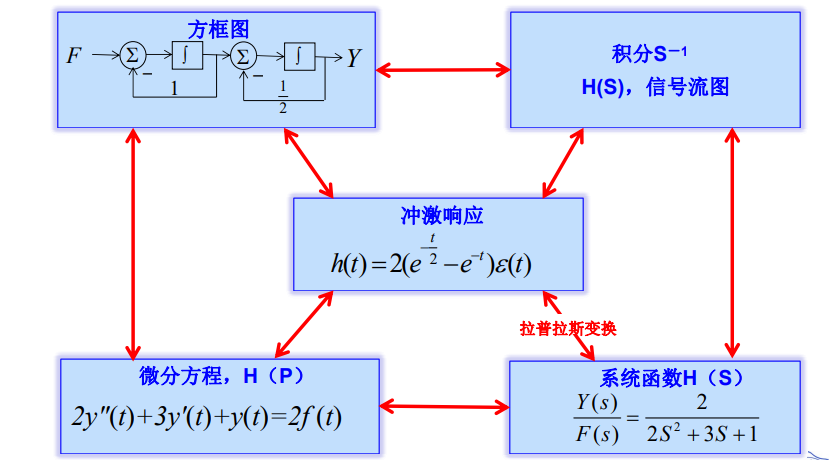
连续系统不同描述方法的关系：

3 $H(S)$的零极点分布与时域特性

3.1 系统函数的零点与极点

零点用⭕表示；极点用❌表示。

极点：$s=-1\pm j2$

3.2 系统函数$H(s)$与时域响应$h(t)$

讨论冲激响应的函数形式与H(s)的极点关系？

对于连续因果系统，$H(s)$按其极点在$s$平面上的位置可分为:在左半开平面、虚轴和右半开平面三类

（1）极点在左半开平面

响应函数衰减。

响应函数震荡衰减。

以上三种情况：当$t\to \infty$时，响应均趋于0，属暂态分量

（2）极点在虚轴上

（3）在右半开平面

均为递增函数

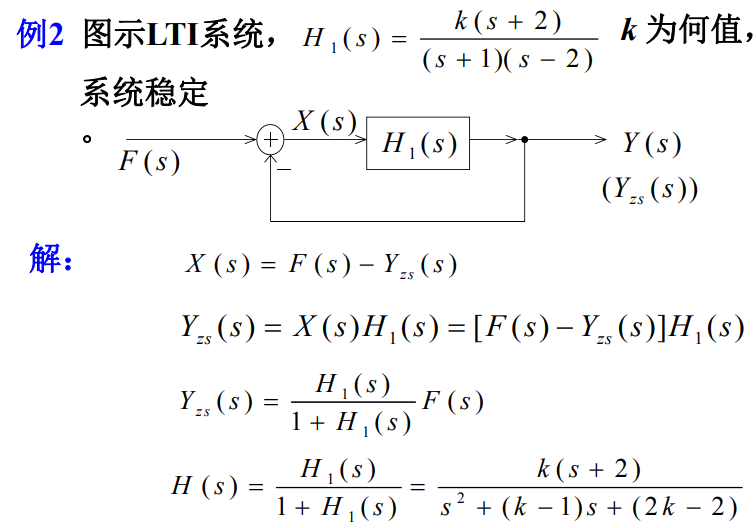
4 连续系统稳定性判别

1.连续系统稳定的充分必要条件是绝对可积：

若$H(s)$的收敛域包含$jw$虚轴，则该系统必是稳定系统。

2.连续因果系统稳定的充分必要条件是

系统左半开平面的极点对应的响应为衰减函数，故，
若$H(s)$的极点均在左半开平面，则该系统必是稳定的
因果系统

3. 稳定系统的 S 域判别方法

5 系统函数与系统的频率特性

1. $H(s)$ 与 $H(j\omega )$ 关系

2. $H(s)$ 零、极点与连续系统频率特性

系统幅频特性与零点无关，与极点有关。

$H(w)$：零点模值相乘除极点模值相乘。

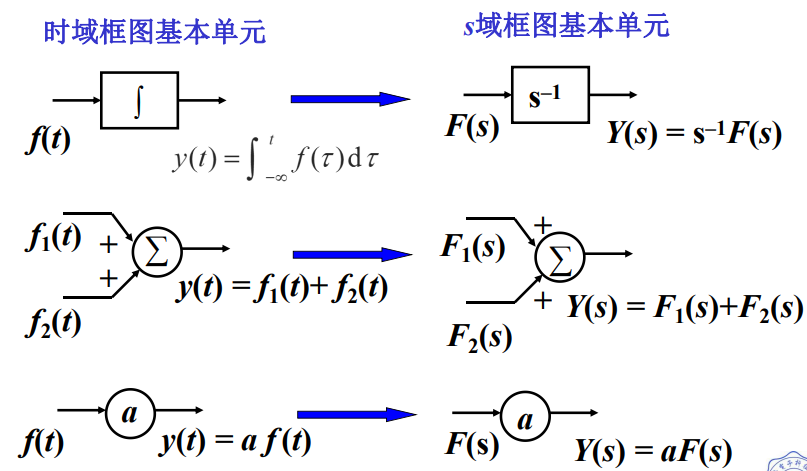
6 连续系统的s域框图

积分器比微分器稳定，所以现实中常用积分器代替微分器。

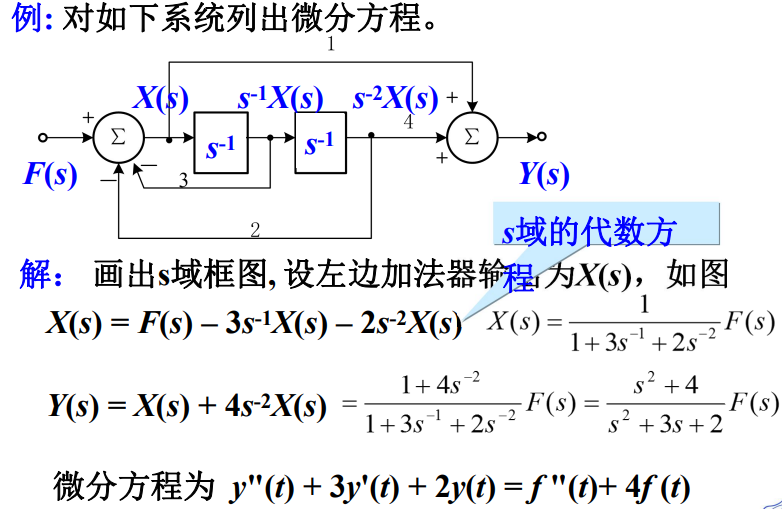
（1）选择求和器的输出$X(s)$作为中间变量

（2）对求和器输入输出$X(s)$列方程

（3）写出$Y(s)$和$X(s)$关系式

（4）整理得到$Y(s)$表达式

（5）写出微分方程

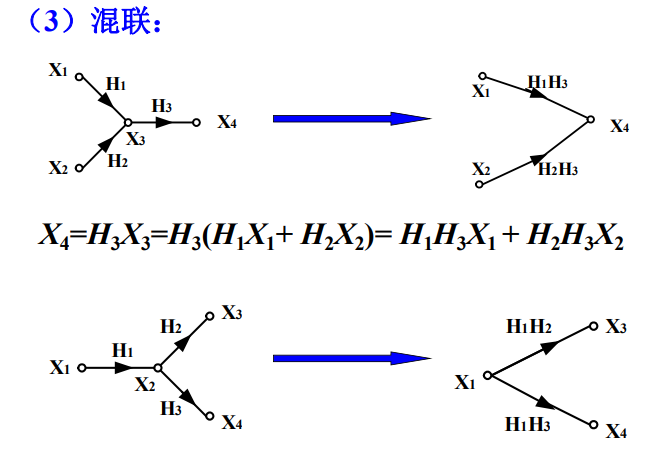
7 连续系统的信号流图

信号流图是系统方框图简化的表示方法。

1.定义 ：信号流图是由结点和有向线段组成的几何图形。它可以简化系统的表示，并便于计算系统函数。

2.信号流图中常用术语

说明：纯粹地记忆这些概念没什么意义，可以通过例题来理解。

(1)结点： 信号流图中的每个结点

(2)支路和支路增益：

连接两个结点之间的有向线段称为支路。每条支路上的权值（支路增益）就是该两结点间的系统函数（转移函数）。

即用一条有向线段表示一个子系统

(3)源点与汇点，混合结点：

仅有出支路的结点称为源点（或输入结点）。
仅有入支路的结点称为汇点（或输出结点）。
有入有出的结点为混合结点 。

(4)通路、开通路、闭通路、不接触回路、自回路

通路－沿箭头指向从一个结点到其他结点的路径。

开通路－如果通路与任一结点相遇不多于一次。

闭通路－若通路的终点就是通路的起点（与其余结点相遇不多于一次。)

不接触回路－相互没有公共结点的回路。

自回路－只有一个结点和一条支路的回路。

(5)前向通路，前向通路增益，回路增益：

前向通路－从源点到汇点的开通路。
前向通路增益－前向通路中各支路增益的乘积。
回路增益－回路中各支路增益的乘积。

3.信号流图的基本性质

（1）信号只能沿支路箭头方向传输。

支路的输出=该支路的输入与支路增益的乘积。

（2）当结点有多个输入时，该结点将所有输入支路的信号相加，并将和信号传输给所有与该结点相连的
输出支路。

4.方框图$\leftrightarrow$流图

注意：加法器前引入增益为1的支路

5.流图的基本规则

8 梅森（Mason）公式

系统函数$H(s)$记为$H$。梅森公式为：
$$H=\frac{1}{\Delta }\sum _i{p}_i{\Delta }_i$$

剩余特征多项式：用与特定前向通路不相交的回路计算。

9 连续系统的模拟

由系统函数画流图

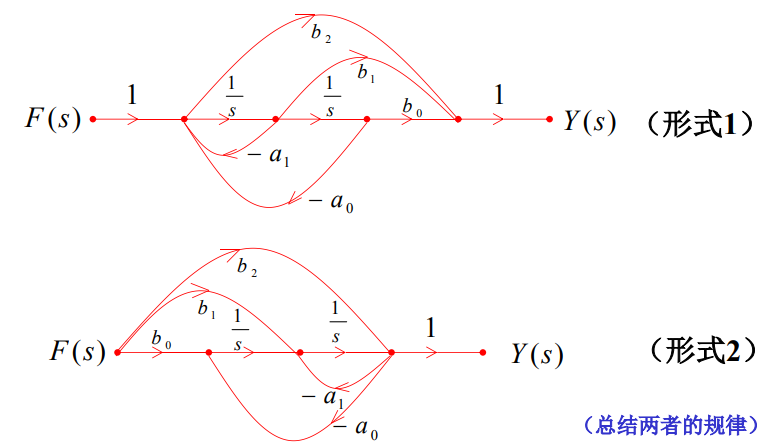
9.1 直接形式

分子中每项看成是一条前向通路。分母中，除1之外，其余每项看成一个回路。画流图时，所有前向通路与全部回路相接触。所有回路均相接触。

由梅森公式：流图包含两条开路，一个环。

（1）画出$s^{-1}$
（2）确定输入输出
（3）根据分母h画环：$\frac{-a_0}{s}$
（4）根据分子画通路

两种形式区别：环和通路公共点不同

（1）画出$s^{-1}$
（2）确定输入输出
（3）根据分母构造环：$\frac{-a_1}{s}$，$\frac{-a_0}{s^2}$
（4）根据分子画通路

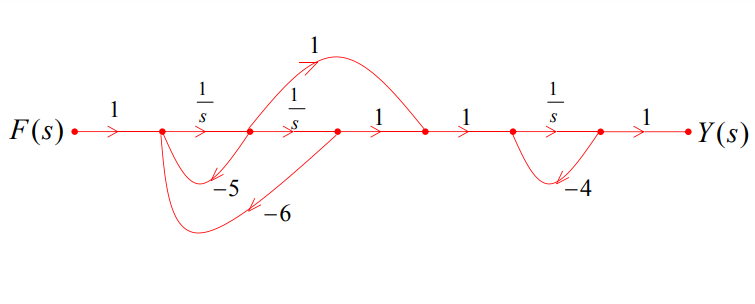
9.2 级联形式

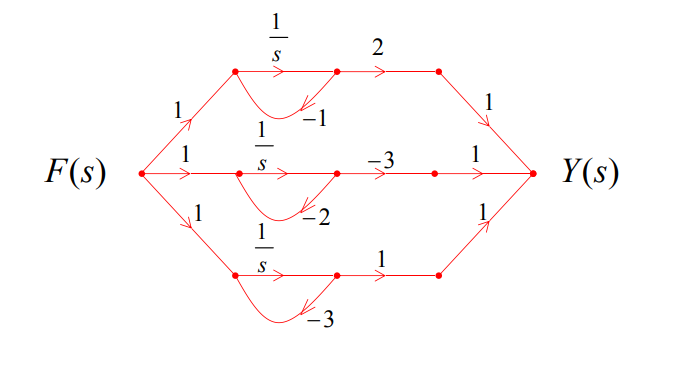
9.3 并联形式

10 零极点配置的作用

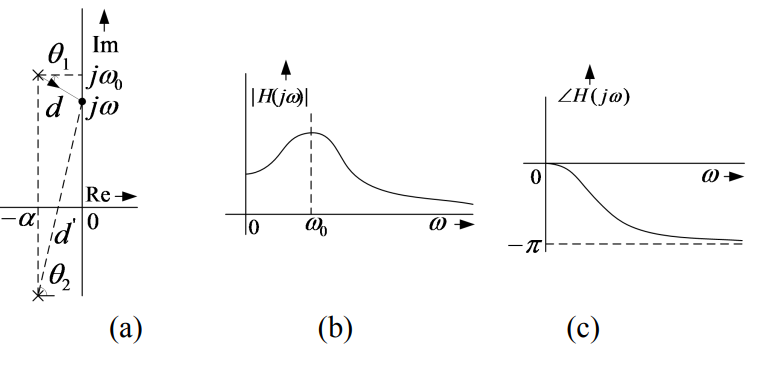
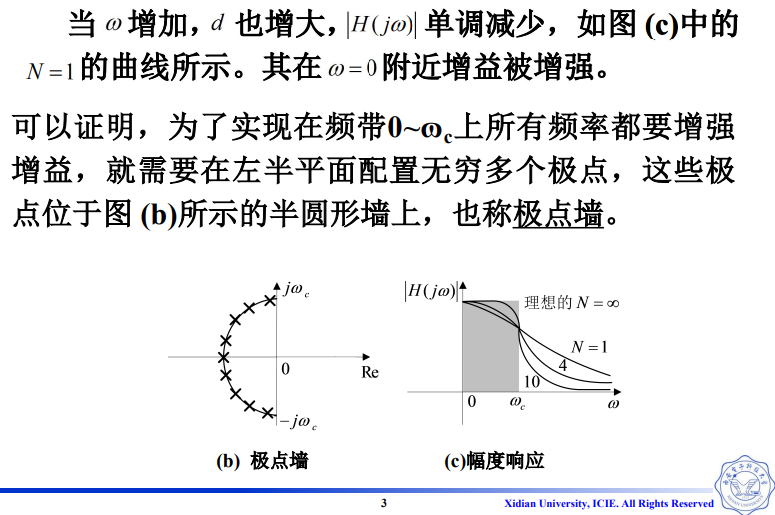
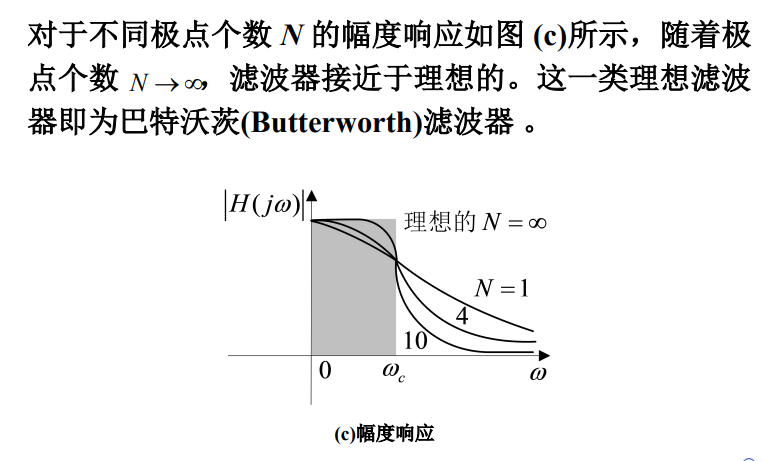
10.1 极点增强效益

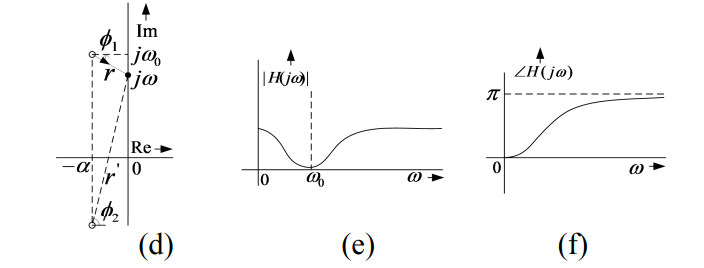
10.2 零点抑制效益

适当配置零极点对，可以互相抵消在频率响应上的影响，因此，可以利用这些不同的频率选择特性，来观察结果，设计低通、高通、带通和带阻（陷波）滤波器。

11 低通、带通、带阻滤波器中零极点的配置

11.1 低通滤波器

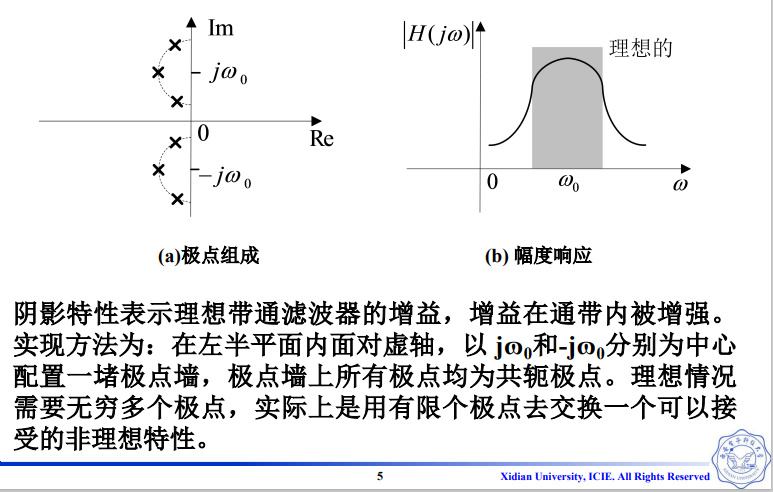
11.2 带通滤波器

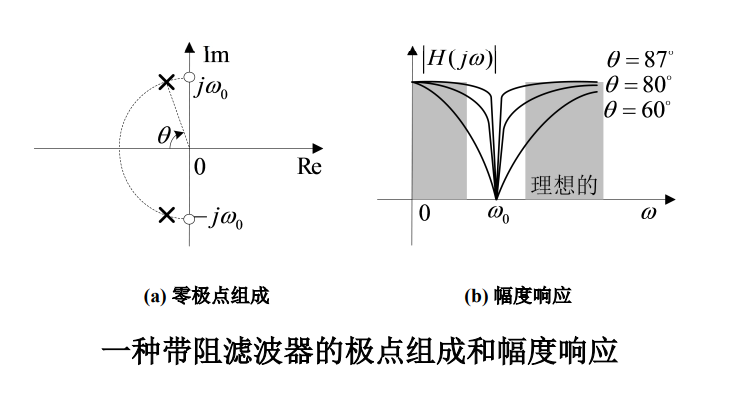
11.3 带阻滤波器

中国大学MOOC：信号与系统 ，西安电子科技大学，郭宝龙，朱娟娟

今天的文章周期信号的拉普拉斯变换咋求_周期信号的拉普拉斯变换咋求分享到此就结束了，感谢您的阅读。