数据结构中的堆是什么意思_数据结构筛选法建立初始堆

一、堆

在C语言中，堆（Heap）是一种基于二叉树结构的数据结构。与内存中的堆不同，此处的堆是指堆数据结构。

1.1 堆的概念

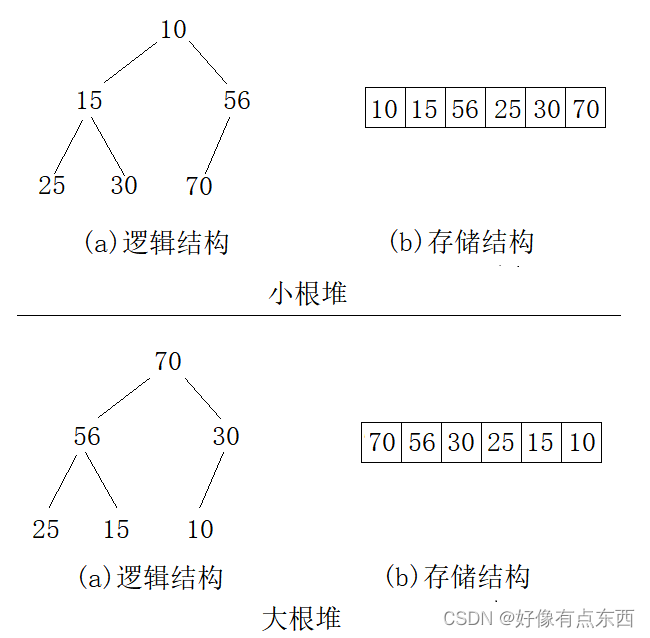
堆是一种特殊的二叉树，它满足两个性质：

堆总是一棵完全二叉树：除了最后一层外，其他层的节点数都是满的，最后一层的节点都尽量靠左排列。

堆中每个节点的值都满足堆的性质：堆中某个节点的值总是不大于或不小于其父节点的值。最大堆又称大根堆(Max Heap)，父节点的值大于等于其子节点的值；最小堆又称小根堆(Min Heap)，父节点的值小于等于其子节点的值。

1.2 堆的结构性质

堆是一种基于二叉树结构的数据结构，一般使用数组来实现，因为对于完全二叉树来说，可以利用数组的索引来表示节点之间的关系。

通常，堆具有以下性质：

根节点索引一般为0

对于堆中其余的任意节点i，它的左孩子节点为2i+1，右孩子节点为2i+2，父节点为(i-1)/2。

每个节点的左右子树也必须是一个堆

小堆不是升序，大堆不是降序

1.3 堆的实现

1.3.1 向上调整

向上调整通常在插入元素到堆中后使用，以确保新插入的元素满足堆的性质。

具体步骤如下：

将新插入的元素放置在堆的最后一个位置（通常是数组的末尾）。

将该元素与其父节点进行比较。

若该元素大于（或小于，具体根据堆是最大堆还是最小堆而定）其父节点的值，则交换该元素和其父节点的位置。

继续向上对比和交换，直到满足堆的性质或达到堆的根节点。

void AdjustUp(HPDataType* arr, int child)
{
	assert(arr);
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (arr[child] < arr[parent])
		{
			swap(&arr[child], &arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

1.3.2 向下调整

给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆（或大堆）。向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

具体步骤如下：

从堆顶元素开始，将其与其子节点中较大（或较小）的节点进行比较。

若堆顶元素小于（或大于，具体根据堆是最大堆还是最小堆而定）其子节点的值，则将其与较大（或较小）的子节点进行交换，并继续向下比较和交换。

继续向下对比和交换，直到满足堆的性质或达到堆的末尾。

void AdjustDown(HPDataType* arr,int size, int parent)
{
	assert(arr);
	HPDataType child = parent * 2 + 1;
	
	while (child < size)
	{
		if (child + 1 < size && arr[child + 1] < arr[child])
		{
			child++;
		}
		if (arr[child] < arr[parent])
		{
			swap(&arr[parent], &arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}

}

1.3.3 创建堆：

步骤如下：

创建一个空堆，可以使用一个数组来存储堆的节点，并初始化堆的大小为0。

一般使用自底向上的方式构建堆，从最后一个非叶子节点开始，依次向上进行堆调整操作。（也可以使用依次插入元素建堆）

//小堆
typedef int HPDataType;
typedef struct {
	HPDataType* a;
	int size;
	int capacity;
}hp;

//初始化堆
void HpInit(hp* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

//创建堆
void HPCrearK(HPDataType* arr, int len)
{
    assert(arr);
	int parent = ((len - 1) - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(arr, len, parent);
		parent--;
	}
}

1.3.4 插入元素：

基本思想：

将一个新的元素插入到堆中，保持堆的性质。

步骤如下：

将新的元素插入到堆的末尾

依次与父节点比较，进行交换操作(向上调整)，

重复2，直到满足堆的性质。

//插入元素
void HpPush(hp* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int NewCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * NewCapacity);
		if (tmp == NULL)
		{
			perror("malloc error!");
			return;
		}
		php->a = tmp;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size-1);

}

1.3.5 删除元素：

删除元素时，通常删除堆顶元素。将堆顶元素与数组末尾的元素交换，然后删除末尾元素，并调整堆的结构，确保堆继续满足堆的性质。

//判空
bool HpEmpty(hp* php)
{
	assert(php);
	return php->size == 0;
}

//交换元素
void swap(HPDataType* a1, HPDataType* a2)
{
	HPDataType tmp = *a1;
	*a1 = *a2;
	*a2 = tmp;
}

//删除堆顶元素
void HpPop(hp* php)
{
	assert(php);
	assert(!HpEmpty(php));
	swap(&php->a[0] , &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

1.3.6 堆排序：

利用堆进行排序的方法称为堆排序。

具体步骤：

将待排序的数组构建成一个堆（向下调整）

从后向前依次堆顶元素放入数组中，并删除堆顶元素

重复2，直至最终得到排序好的数组。

//堆排序
void HpSort(HPDataType* arr, int len)
{
	assert(arr);
	int parent = ((len - 1) - 1) / 2;
	while (parent >= 0)
	{
		AdjustDown(arr, len, parent);
		parent--;
	}

	int end = len - 1;
	while (end > 0)
	{
		swap(&arr[0], &arr[end]);

		// 再调整，选出次小的数
		AdjustDown(arr, end, 0);

		end--;
	}
}

1.4 堆的应用

1.4.1 Top K 问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

具体步骤如下：

用数据集合中前K个元素来建堆
前k个最大的元素，建小堆
前k个最小的元素，则建大堆

用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

//创建大小为K的堆
hp* HPCrearK(int k)
{
	hp* tmp = (hp*)malloc(sizeof(hp));
	if (tmp == NULL)
	{
		perror("malloc error!");
		return NULL;
	}
	HpInit(tmp);
	HPDataType* arr = (HPDataType*)malloc(sizeof(HPDataType) * k);
	if (arr == NULL)
	{
		perror("malloc error!");
		return NULL;
	}
	tmp->a = arr;
	tmp->capacity = k;
	return tmp;
}

//Topk
HPDataType TopK(HPDataType* arr, int k, int len)
{
	assert(arr);
	if (k > len)
	{
		return EOF;
	}
	hp* php = HPCrearK(k);
	if (php == NULL)
	{
		perror("Creat error");
		return EOF;
	}
	for (int i = 0; i < k; i++)
	{
		HpPush(php, arr[i]);
	}
	for (int i = k; i < len; i++)
	{
		if (arr[i] > HpTop(php))
		{
			HpPop(php);
			HpPush(php, arr[i]);
		}
	}
	return HpTop(php);
}

今天的文章数据结构中的堆是什么意思_数据结构筛选法建立初始堆分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/81935.html